
Презентация "Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a"

Краткое описание документа:
Изучение таких понятий, как арктангенс и арккотангенс, входит в раздел тригонометрии. Необходимо понимать эти определения, разобраться в геометрическом смысле.
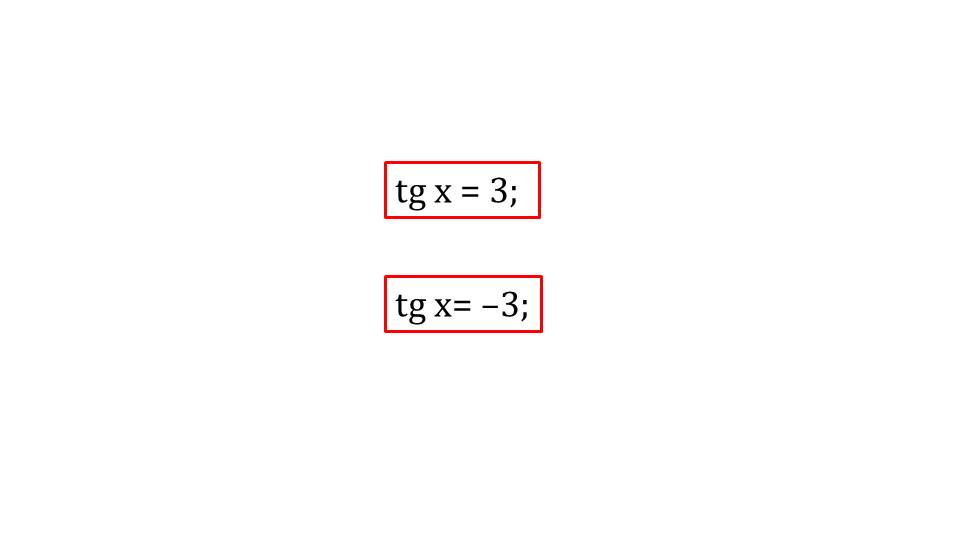
Данная презентация раскроет тему «Арктангенс и арккотангенс» и покажет, как необходимо решать уравнения, в которых неизвестные заключены в тангенс или в котангенс.

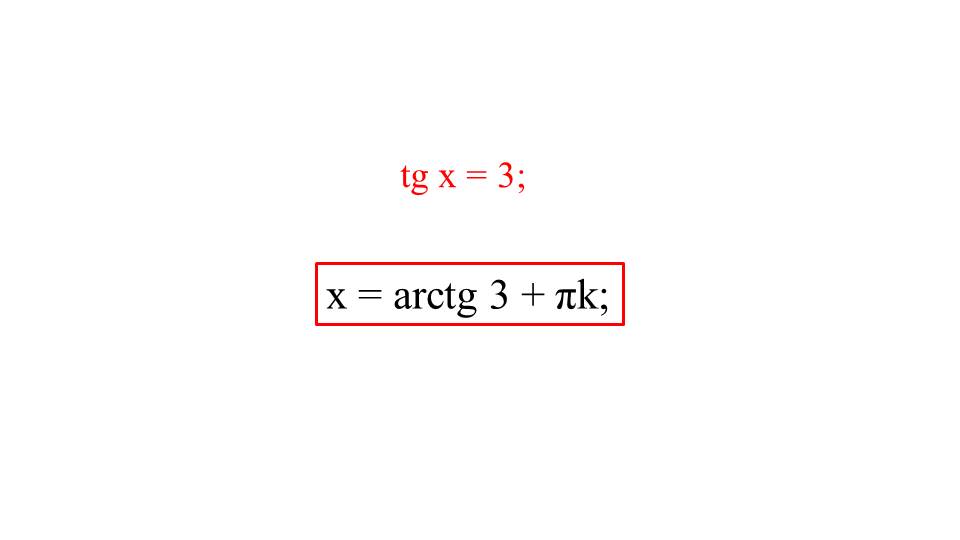
Презентация включает в себя 21 слайдов, которые построены очень грамотно, содержать понятные иллюстрации, которые помогут лучше запомнить некоторые важные выражения и формулы.
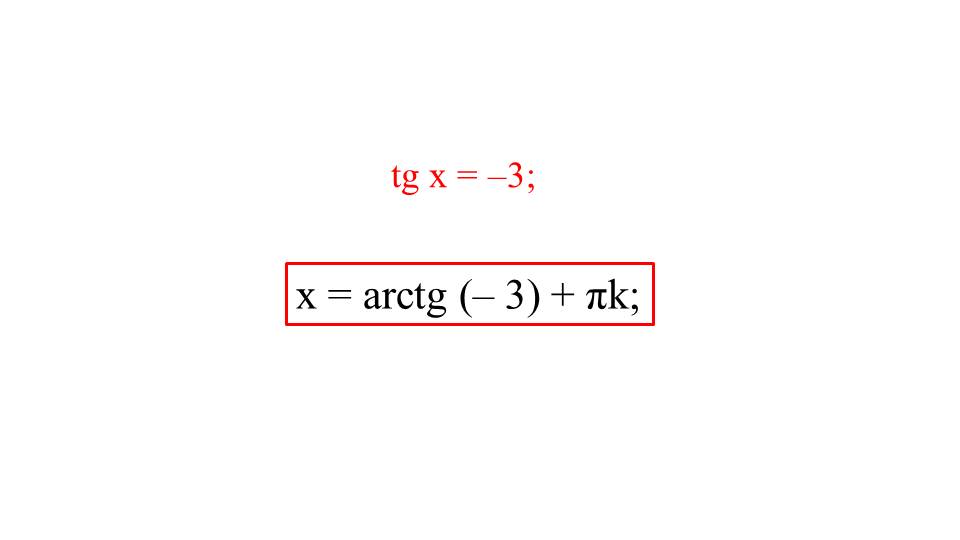
На первом слайде выводятся два уравнения, в которых необходимо найти тангенс какого числа будет равняться 3 и -3.
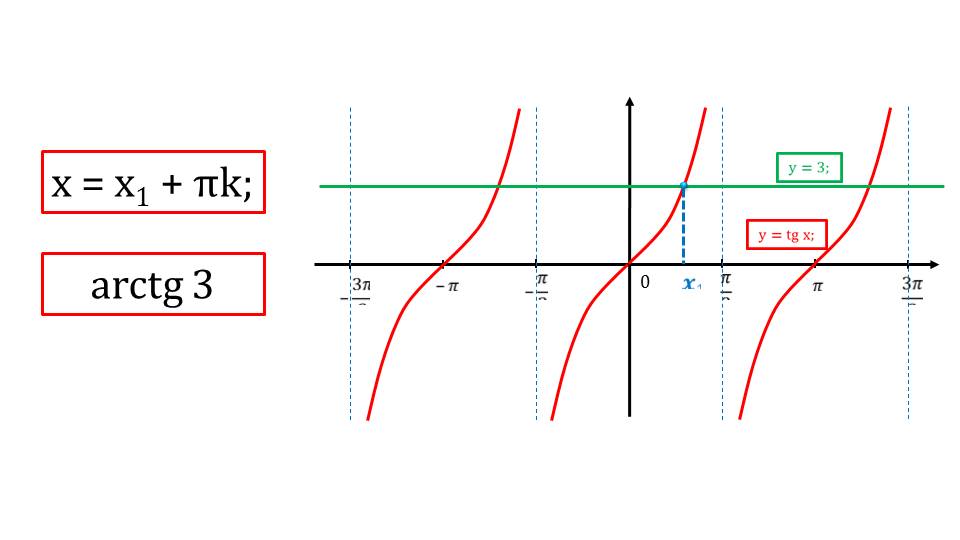
На первом этапе решение приводится геометрически. То есть проводятся построение периодического графика функции у=tgx и у=3. Пересечение этих графиков и покажет нам корни данного уравнения.
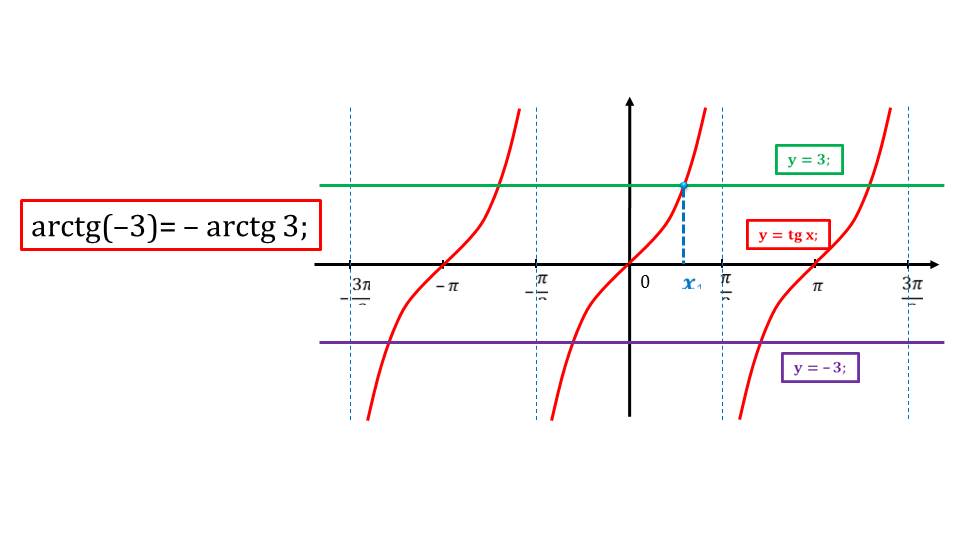
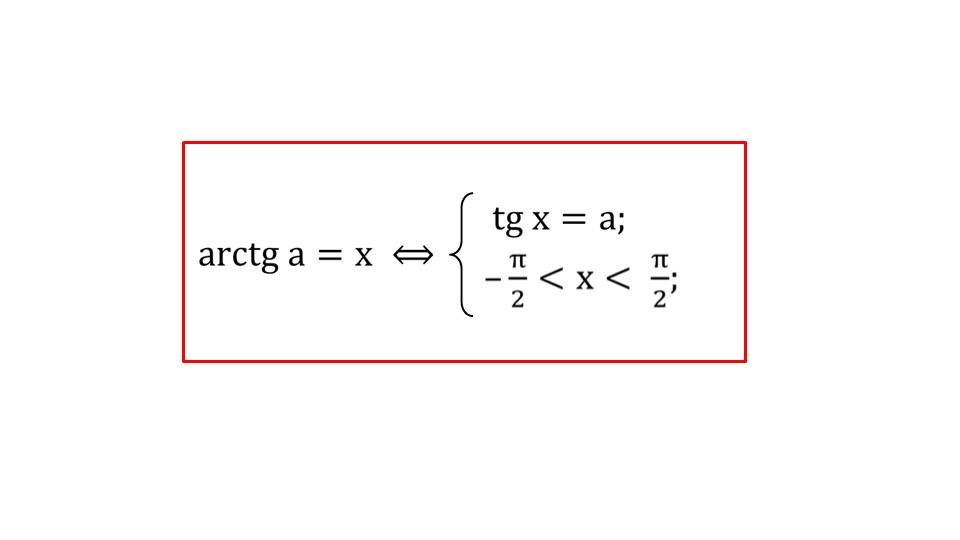
Так как график функции тангенса является периодической, а прямая растянута по всей числовой оси, пересечений получится бесконечно количество. Для того чтобы записать ответ используется периодическая запись в общем виде.
О том, как понять смысл записи arctg3, говорится на следующем слайде.
[img]/jpg/Arktangens_i_arkkotangens._Reshenie_uravnenij_tgx_=_a,_ctgx_=_a_10.9.jpg/img][img]/jpg/Arktangens_i_arkkotangens._Reshenie_uravnenij_tgx_=_a,_ctgx_=_a_10.10.jpg[/img]
Все аналогично арккосинусу и арксинусу.
Далее выводится решение предыдущего примера в общем виде вместе с периодом Пиk.
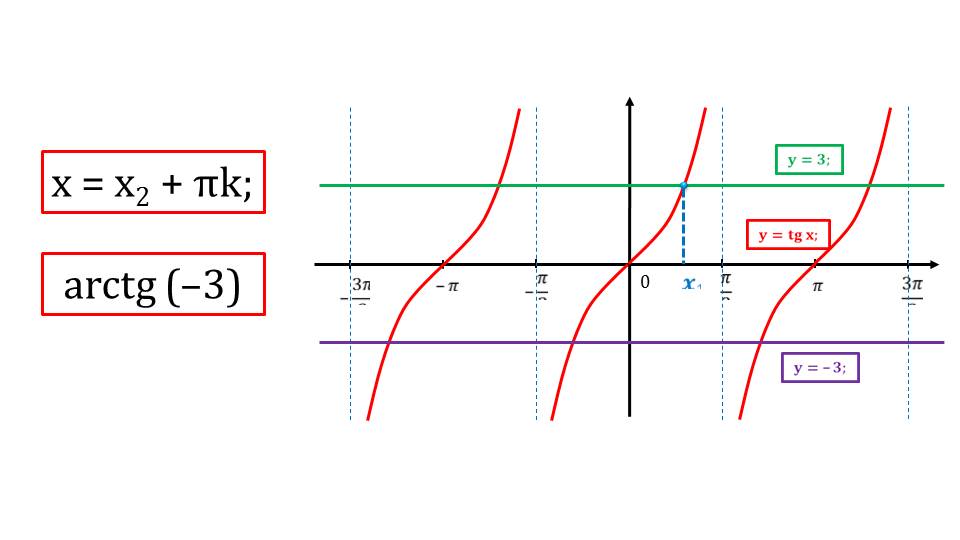
Каким же будет решение при втором уравнении. Решение приводится на последующем слайде. Предыдущие графики остались на иллюстрации для сравнения.

Далее приводится обобщенный вид решения тригонометрического уравнения. Указывается, что неизвестный аргумент заключен в интервал [-Пи/2; Пи/2].

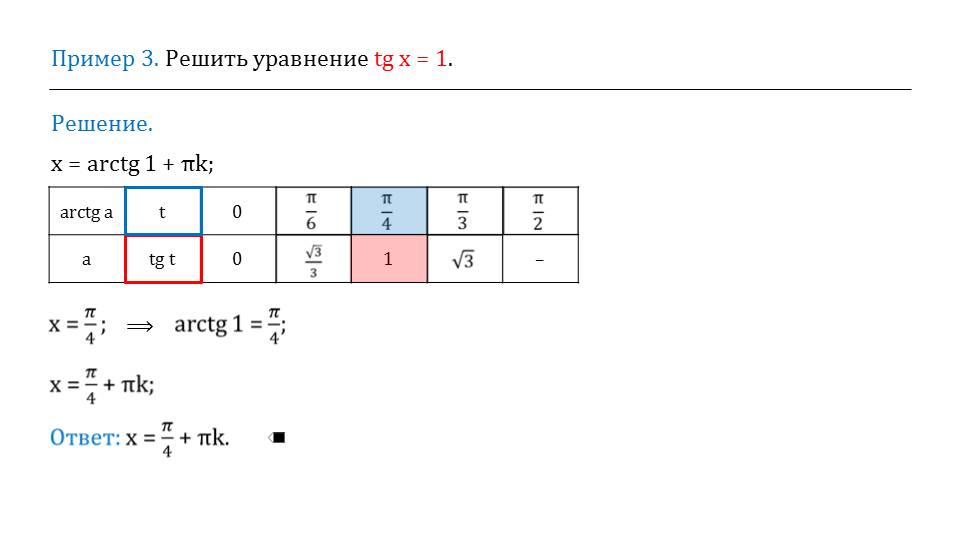
После этой части рассмотрения темы, на слайды выводятся примеры. Их можно решить в классе или дать школьникам в виде домашнего задания.

Если они с ними разберутся, то смогут решить подобные задания и на самостоятельных работах.
Второе свойство, которое выводится на 15 слайде говорит о том, что функция тангенса является периодической. Основной период составляет Пи.

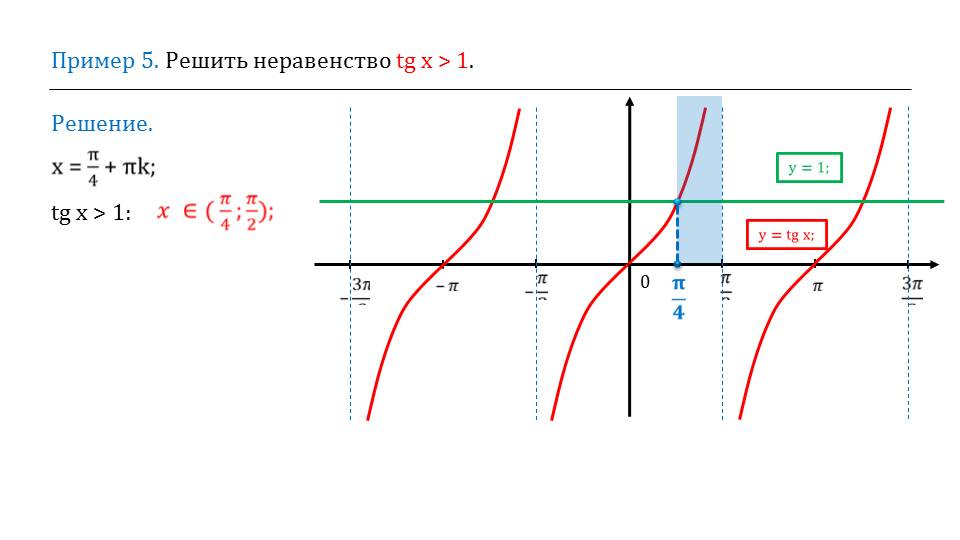
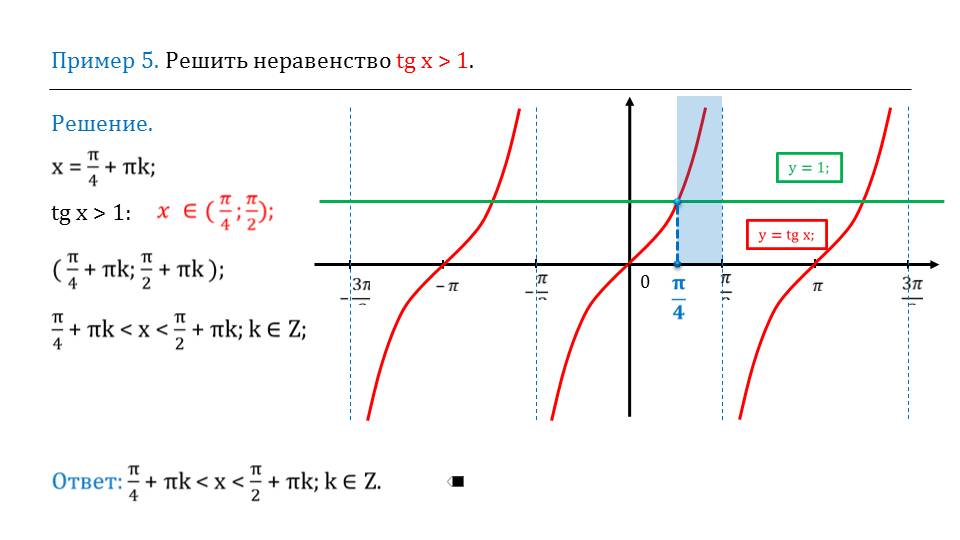
После того, как рассмотрены решения уравнений, пора перейти к решению неравенств, которые содержат тангенсы. Приводится пример.
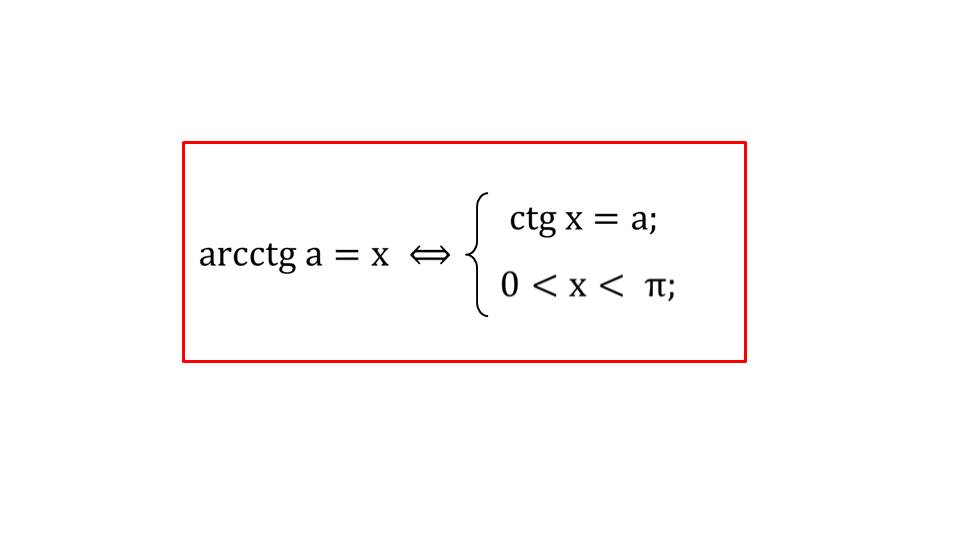

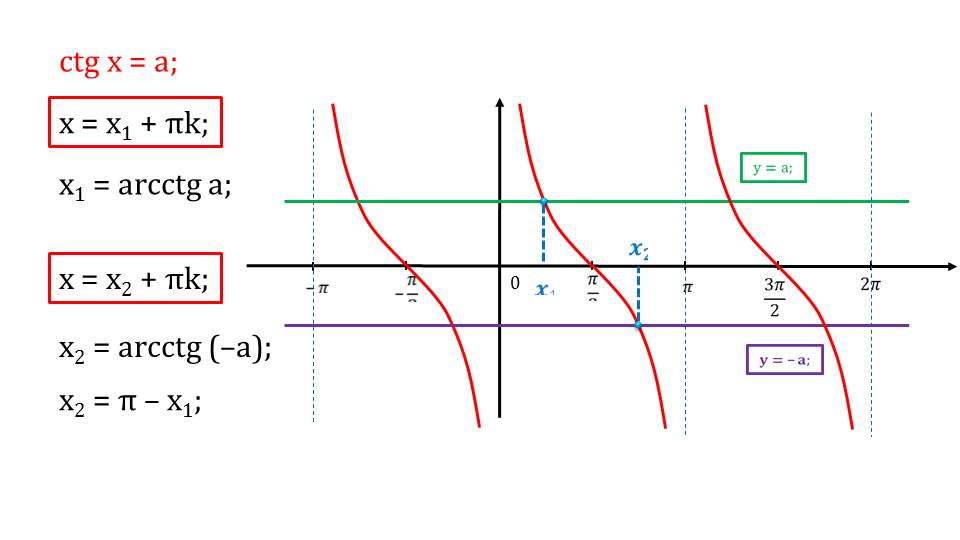
Далее рассматривается функция котангенса, строится его график и демонстрируется решение уравнений, содержащие котангенсы. Они аналогичны предыдущим примерам и будут понятны 10-класснику.
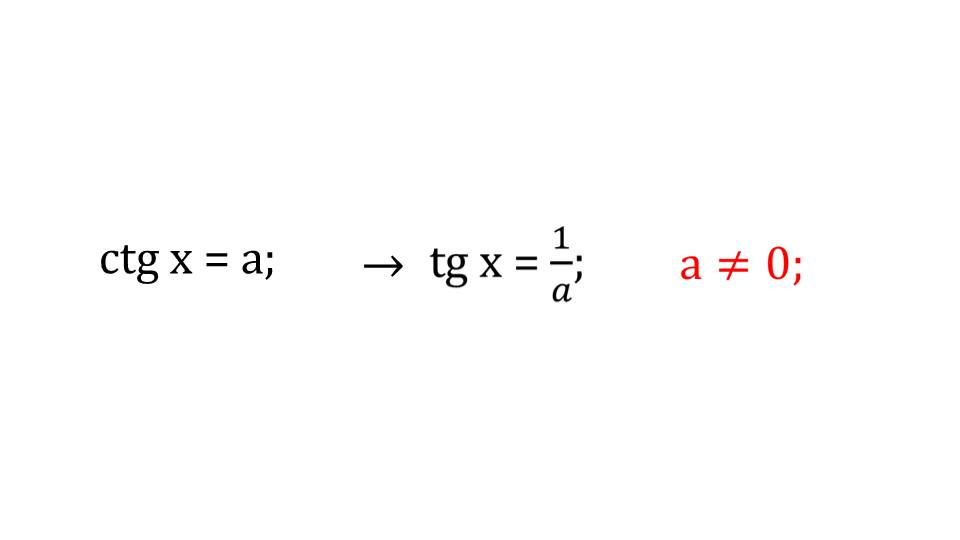
На завершительном этапе презентации указывается важный момент: арккотангенс можно вывести через арктангенс. При некоторых вычислениях это упростит задачу.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7370 |
| Номер материала | 808 |