
Презентация "Число е. Функция у=ех, ее свойства, график, дифференцирование"

Краткое описание документа:
Данная презентация посвящена теме «Число е. Функция у=ех, ее свойства, график, дифференцирование». Благодаря ней можно составить интересный урок, продемонстрировать ученикам практически примеры и рассказать о теоретических фактах, свойствах некоторых функций, показать визуально графики.


Урок, которому посвящена данная презентация, является логическим продолжением предыдущих. Конечно. Он частично будет понятен при просмотре и рассматривании, однако, для тог, чтобы добиться максимальной эффективности, желательно, вспомнить предыдущий, просмотреть предыдущую презентацию.
Презентацию можно демонстрировать во время урока, если в классе есть необходимое оборудование для ее просмотра. Это поможет улучшить процесс обучения, позвлит учителю быть довольным проведенным уроком, увидеть определенные результаты.

При выполнении домашнего задания, школьники могут воспользоваться данным материалом в качестве вспомогательного.
Начинается презентация на тему «Число е. Функция у=ех, ее свойства, график, дифференцирование» с напоминания значение числа е, которое составляет приблизительно 2,72. На слайде приведено более точное значение данной константы.
Далее, предлагается школьникам найти производную от некоторого дробного выражения, которое содержит тригонометрические функции. Решив данный пример, ученики возобновят в своей памяти нахождение производных, что понадобится в дальнейшем при изучении данного урока.
Итак, на следующем слайде можно увидеть записанные в столбик некоторые логарифмические выражения. Так как школьники столкнулись с этим впервые, приводятся текстовые объяснение, с помощью которых они могут понять, как необходимо читать данные записи. Как видим, каждое логарифмическое выражение имеет основание и некоторое значение. Логарифм указывает на то, что необходимо найти степень, при котором основание будет равняться значению при логарифме.
Как видим, десятичный логарифм имеет особую запись. Также специальное обозначение имеется для натурального логарифма. Приводятся записи данных понятий в общем виде.


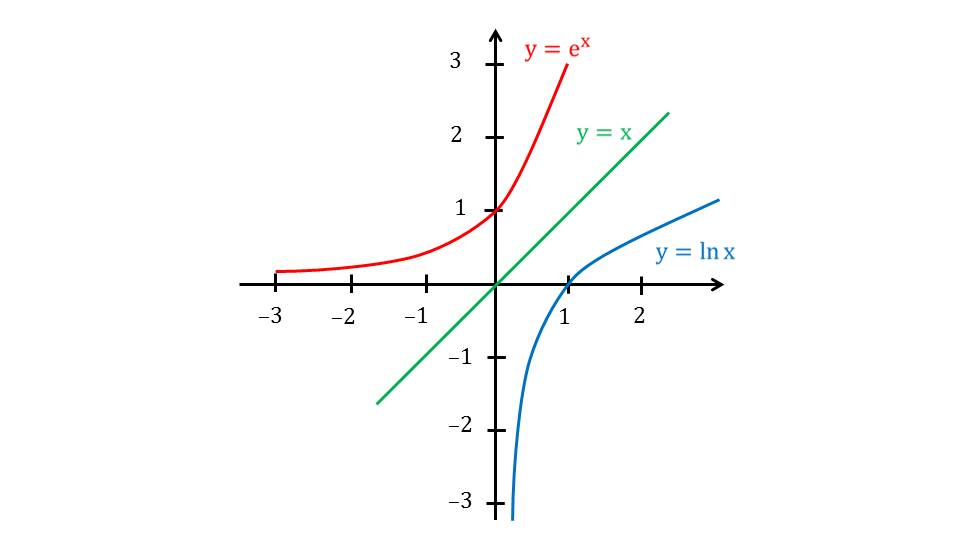
Чтобы увидеть разницу визуально между графиками показательной и логарифмической функции, на одной системе координат приводятся три графика – график функции натурального логарифма, график функции y=x , и график показательной функции, в основании которое стоит константа е, а показателем является х. Нетрудно заменить, что кривые, отвечающие на системе координат за функции показательной и логарифмической функций, являются симметричны относительно прямой, которая является графиком функции у=х.
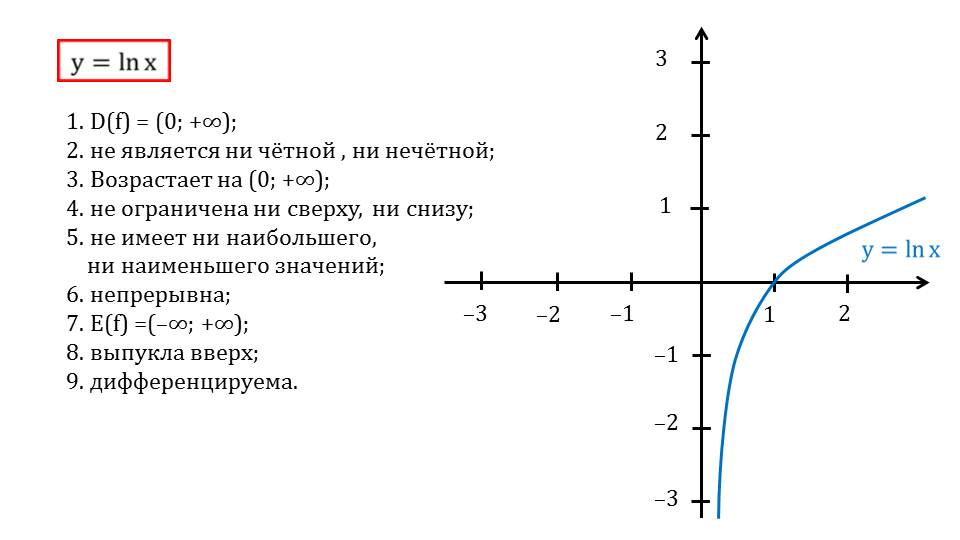
На следующем слайде приводится подробный анализ графика функции натурального логарифма, по всем 9 пунктам. Рассмотрены область определения и значений, исследована на четность и нечетность, монотонность, ограниченность, непрерывность, выпуклость и дифференцируемость. Что касается последнего, то стоит отметить, что функция натурального логарифма является дифференцируемой в каждой токе, ведь она не имеет точек разрыва и является непрерывной.

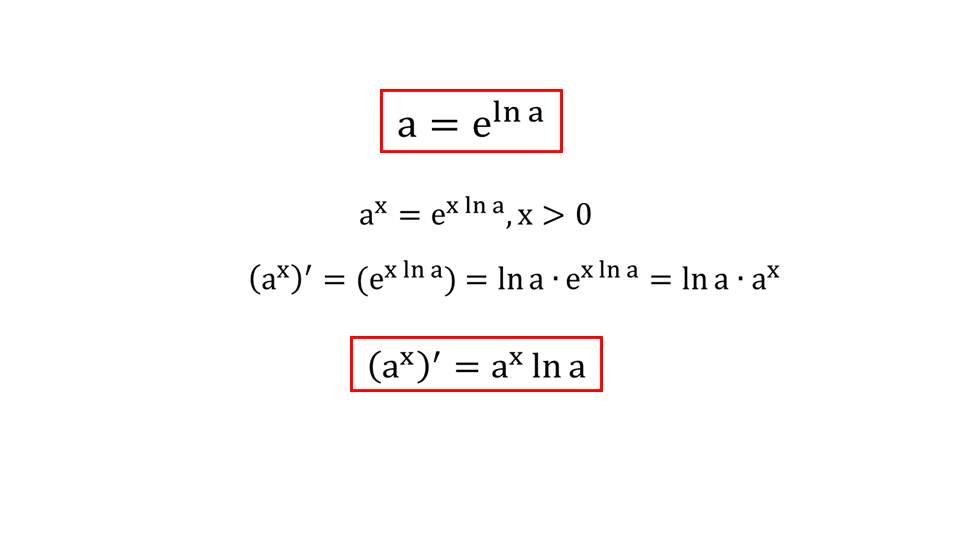
Так как функция является дифференцируемой, имеет смысл рассмотреть это далее более подробно, что собственно и выполняется на следующих слайдах.
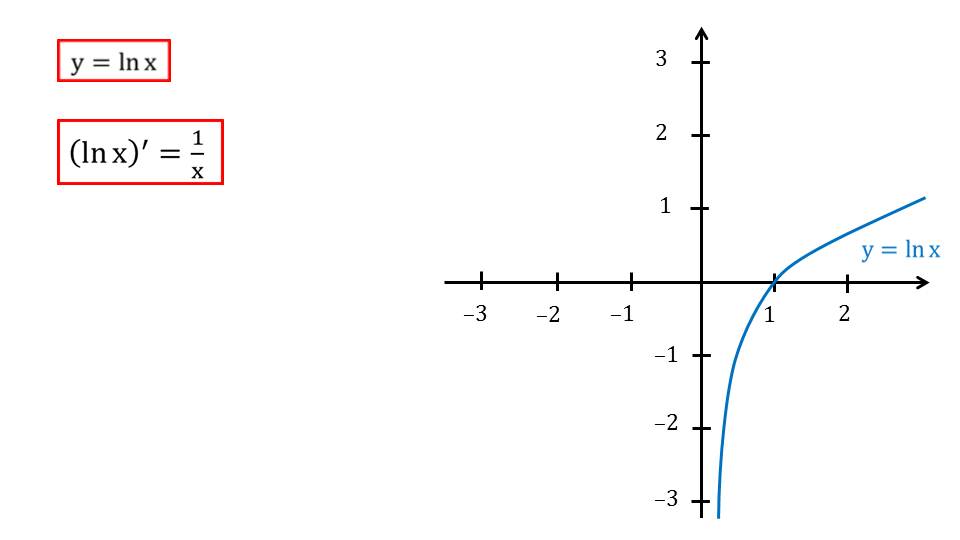
Приводится формула производной от натурального логарифма. Ее достаточно просто запомнить. Стоит также еще раз отметить ,что основанием натурального логарифма является уже ранее рассмотренный коэффициент е.


После некоторых примеров, приводится еще одна важная формула, с помощью которой можно найти производную от показательной функции, в степени контрой содержится натуральных логарифм, а основание является е.
Материал закрепляется опять же примерами, после чего приступаем к изучению нахождения производной от обычной логарифмической функции, отличной от натуральной. То есть основанием является некоторое а. На последнем слайде приводится последний пример.

После изучения темы «Число е. Функция у=ех, ее свойства, график, дифференцирование» необходимо уделить внимание практике, благодаря чему материал может закрепиться в памяти на долгое время.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6588 |
| Номер материала | 1033 |