
Презентация «Сложение и умножение вероятностей»

Краткое описание документа:
Презентация «Сложение и умножение вероятностей» представляет наглядный учебный материал для освоения данной темы. Эта тема важная для решения практических задач по нахождению значения вероятностей, которые определяются в ходе сложения или умножения вероятностей. Тема сложная, поэтому требует высокой концентрации внимания учеников на уроке, глубокого понимания процессов нахождения вероятностей, выполнения операций с ними.

Приемы, используемые в презентации, позволяют более эффективно добиться целей урока. При помощи иллюстраций и анимационных эффектов можно добиться высокой реалистичности наблюдаемых опытов, чтобы выводы были сделаны в ходе рассуждений самим учеником. Для лучшего понимания и запоминания материала также используется выделение цветом, рамкой важных понятий и формул.


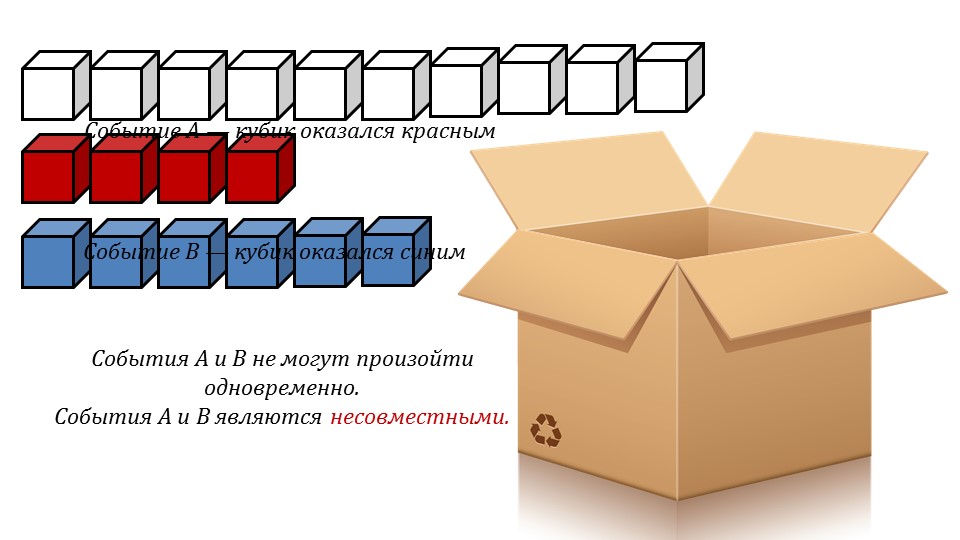
Презентация начинается с представления темы, после чего при помощи анимации представлена задача. В коробку сложены кубики, 10 из которых белые, 4 – красные, 6 – синие. После помещения кубиков в коробку они вынимаются по одному. При этом вытягивание красного кубика называется событием A, а вытягивание синего кубика – событием B. Отмечается, что одновременно эти два события не могут произойти, то есть кубик не может быть одновременно и красным, и синим. В теории вероятностей такие события называют несовместными. Данное понятие выделено на экране красным для запоминания, а на следующем слайде 3 выведено определение несовместных событий как событий, которые в одном и том же испытании не могут наступить одновременно, то есть являются взаимоисключающими.
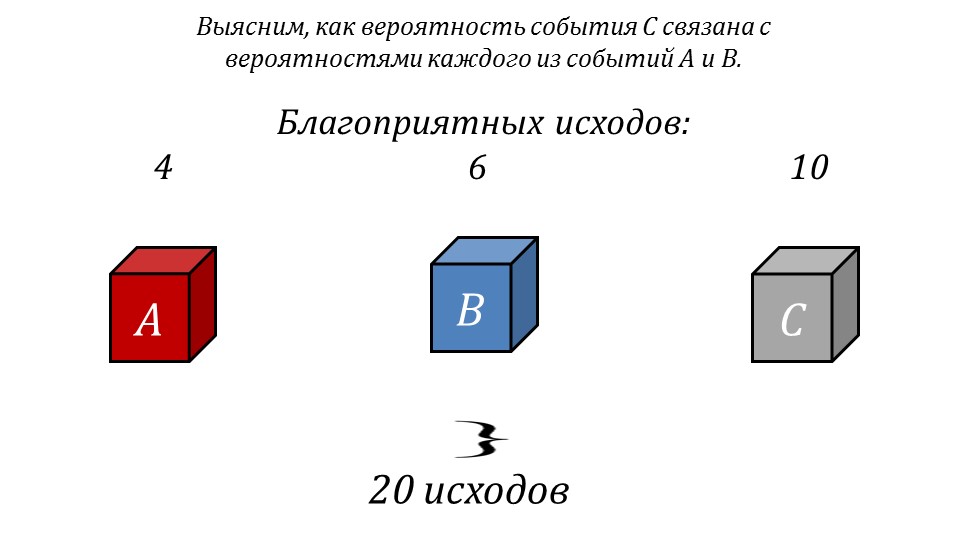
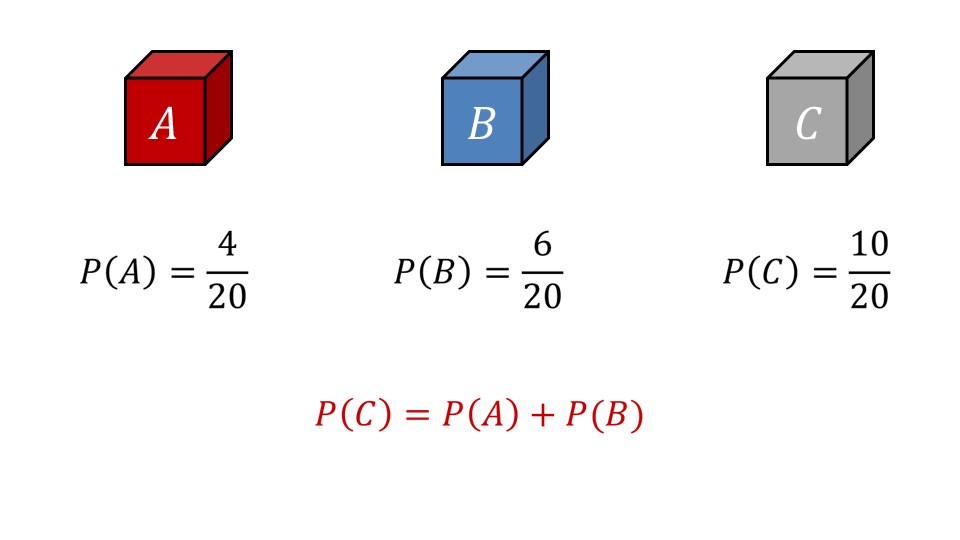
Предлагается рассмотреть вероятности ряда событий, при этом событие A – вынимание красного кубика, событие B – вынимание синего кубика, событие C – вынутый кубик не является белым. Далее рассматривается, каким образом связаны между собой вероятности данных событий. Для этого сначала определяется, сколько может быть благоприятных исходов. В общей сумме количество равновозможных исходов 4+6+10=20. То есть всего возможно 20 исходов. Вероятность наступления события A вычисляется как P(A)=4/20, вероятность наступления события B вычисляется как P(B)=6/20, а вероятность наступления C определяется как P(C)=10/20. При этом видно, что P(C)=P(A)+ P(B). На слайде 7 определяется вероятность события C как суммы вероятностей событий A и B в случае, когда событие C означает, что наступает одно из несовместных событий.

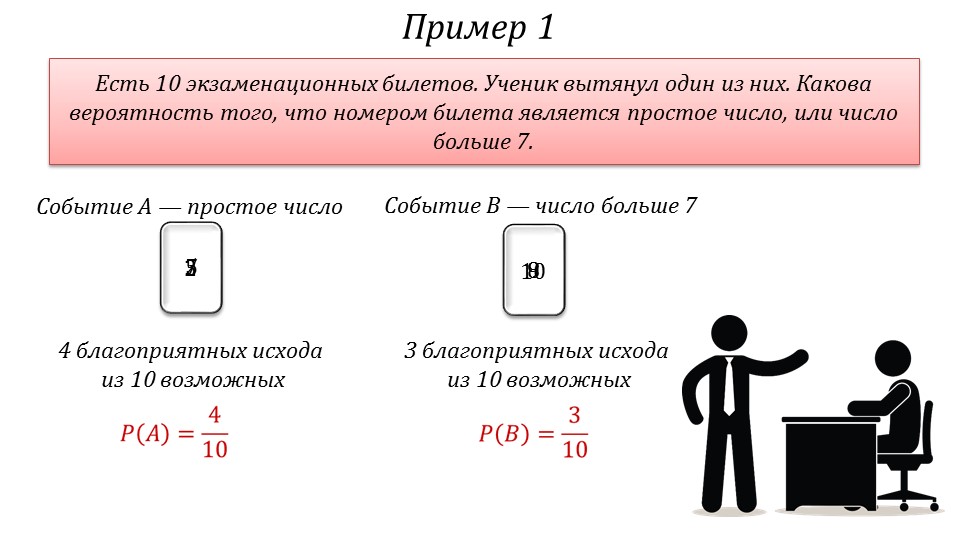
Также рассмотреть сумму вероятностей событий предлагается на примере задачи, в которой нужно найти вероятность вытягивания 1 из 10 экзаменационных билетов, номер которого будет или простым числом, или числом, больше 7. При помощи анимации демонстрируются варианты вытягивания билетов, номер которых является простым числом. Это числа 2, 3, 5, 7. Таким образом, получается 4 благоприятных исхода из 10 возможных. Вероятность их наступления P(A)=4/10. Событие B определяется благоприятными исходами 8, 9, 10.
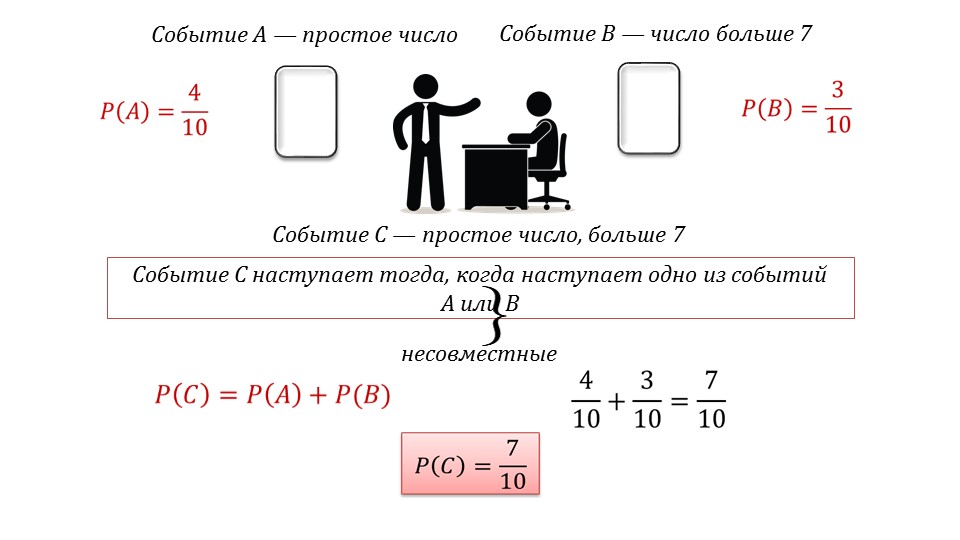
Таким образом, возможно наступление благоприятных 3 из 10 возможных исходов. Вероятность наступления данного события P(B)=3/10. Событие C рассматривается как сумма событий A и B, так как оно означает, что может выпасть билет с номером-простым числом или номером, больше 7. То есть суммирующее событие наступает, когда наступает одно из событий - A или B. В этом случае вероятность события C определяется суммой вероятностей наступления событий A и B: P(C)=P(A)+ P(B). В рассматриваемой задаче такая сумма будет равна 4/10+3/10=7/10. Поэтому вероятность наступления события C равна P(C)=7/10.
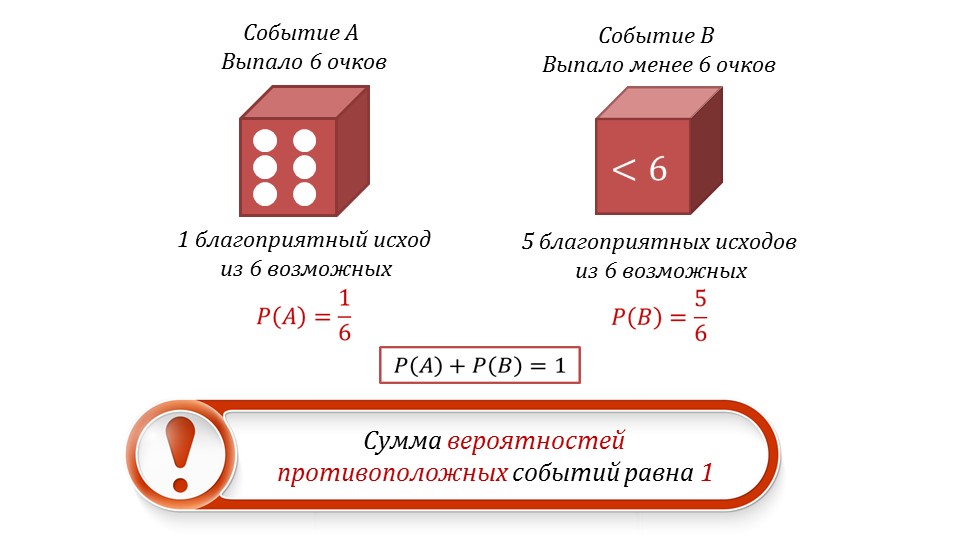

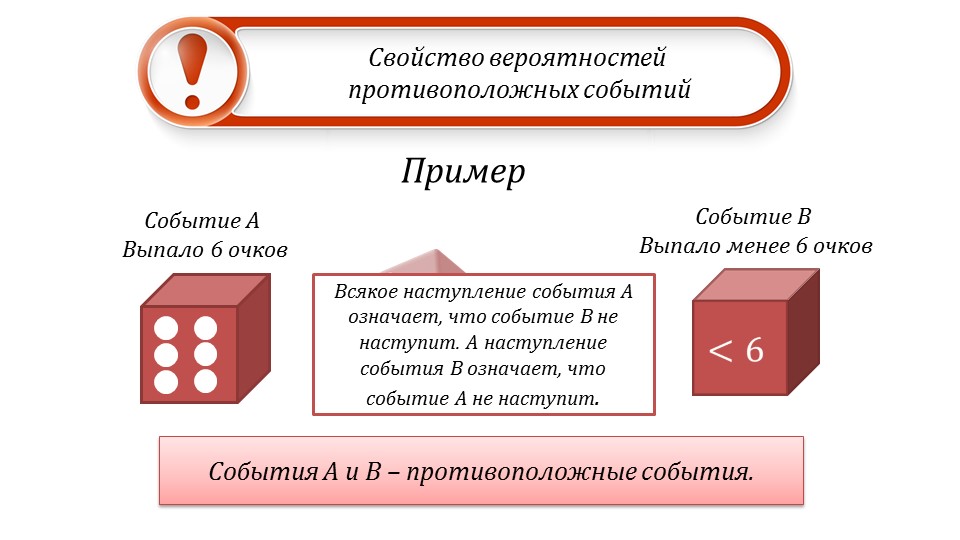
На слайде 10 рассматривается свойство вероятностей противоположных событий на примере задачи. В данной задаче указаны два события – событие A означает, что при подбрасывании игрального кубика, на его грани выпало 6 очков, а событие B означает, что выпало менее 6 очков. Событие A означает, что событие B не наступит, и наоборот, если наступает событие B, то событие A не наступит. Таким образом, события являются противоположными. Рассмотрим их вероятности. На рисунке изображен кубик с 6 очками на грани. Рядом располагается кубик, на котором выпало менее 6 очков. Событие A наступает с вероятностью P(A)=1/6, а событие B наступает 5 случаях из 6 возможных, то есть с вероятностью P(B)=5/6. Общая сумма вероятностей составит P(A)+ P(B)=1. Видно, что сумма вероятностей противоположных событий равняется 1.


На слайде 12 выводится свойство противоположных событий для запоминания. В определении указано, что если в ходе испытания рассматриваются противоположные события A и ¯A. Так как A и ¯A являются несовместными, то наступление хотя бы одного из них – достоверное событие. Поэтому P(A)+ P(¯A)=1.
Свойство противоположных событий применяется при решении задач. Примером решения такой задачи служит рассмотрение хода решения на слайде 13. Необходимо найти вероятность того, что сумма очков на двух кубиках после броска будет не равно 9. Для решения задачи определяется общее число равновозможных исходов – 36. Сначала определим событие A как выпадение суммы очков не равно 9, а событие ¯A как сумму очков равной 9. Исходов с достижением суммы очков 9 может быть 4, поэтому вероятность выпадения 9 очков оценивается как P(¯A)=4/36=1/9. Так как искомое событие противоположное событию ¯A, то его вероятность определяется по формуле P(A)=1-P(¯A)=1-1/9=8/9.


Далее рассматривается более сложный случай – определение вероятностей двух независимых событий. Для этого на слайде 14 определяется понятие независимых событий как событий, среди которых наступление одного события не влияет на наступление другого.
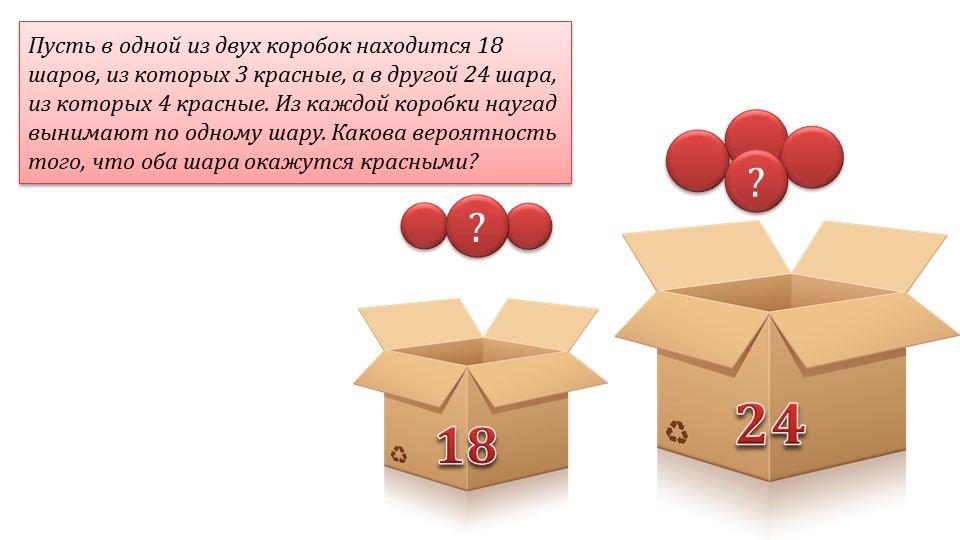
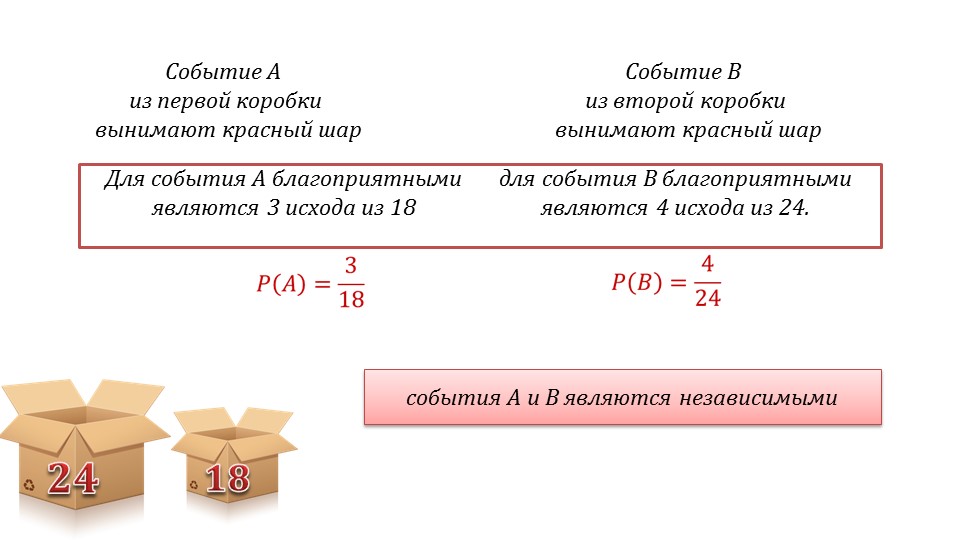
Примером рассмотрения независимых событий служит задача, рассматриваемая на слайде 15. Здесь предлагается рассмотреть вынимание шаров по одному из двух коробок одновременно. При этом известно, что в первой коробке всего 18 шаров, и 3 из них – красные, а во второй коробке 24 шара, из которых 4 красные. Нужно найти вероятность вынимания одновременно двух красных шаров. В задаче рассматриваются отдельно событие A, означающее, что из первой коробки вынут красный шар. Для этого события благоприятных исходов может быть 3 из возможных 18, а вероятность наступления события P(A)=3/18. Событие B, означающее вынимание из второй коробки красного шара, рассматривается независимо от A. Благоприятных исходов для данного события 4 из 24. Это означает, что вероятность наступления события P(B)=4/24. Так как данные события независимы друг от друга, общее число равновозможных событий для события C будет 18•24. При этом благоприятными будут исходы, которые определяются произведением благоприятных событий 3•4. Поэтому вероятность искомого события C определяется произведением вероятностей наступления двух рассмотренных событий: P(C)=(3•4)/(18•24)=3/18∙4/24. Вероятность события C вычисляется по формуле P(C)= P(A)•P(B).
Определение произведения вероятностей событий A и B представлено на слайде 18. В нем произведение вероятностей представлено как вероятность наступления события C, которое означает совместное наступление событий A и B.
В конце презентации рассматривается решение двух задач, в которых необходимо уметь вычислять произведение вероятностей. Первая задача описывает вытягивание карточек с числами из 9 карточек, на которых написаны цифры от 1 до 9. Нужно выяснить, какова вероятность, что вытянутые по одной (первая ложится на место) карточки содержат простые числа. Для событий A (первая карточка с простым числом) и B (вторая карточка с простым числом) вероятности определяются как P(A)=4/9 и P(B)=4/9. При этом для события одновременного вытягивания карточек с простыми числами определяется после вычисления значения произведения P(C)= P(A)•P(B)=4/9•4/9=16/81=0,2.


Во второй задаче даются известные вероятности попадания в мишень двух стрелков – 0,7 и 0,6. Необходимо найти вероятность поражения мишени после того, как каждым стрелком был сделан выстрел. Определяются события A как попадание в мишень первого стрелка, B – попадание в мишень второго стрелка. Общее событие C – поражение мишени. Таким же образом определяются противоположные события. Вероятность противоположных событий P(¯A)=1-0,7=0,3, а P(¯B)=1-0,6=0,4. При этом произведение двух вероятностей как вероятности отсутствия поражения мишени вычисляется P(¯C)=P(¯A)•P(¯B)=0.3•.4=0.12 Поэтому вероятность поражения мишени P(C)=1- P(¯C)=1-0,12=0,88.
Презентация «Сложение и умножение вероятностей» может быть использована на уроке как наглядный материал, а также при дистанционном обучение. Подробное понятное объяснение решения задач может помочь ученикам самостоятельно освоить материал.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 26766 |
| Номер материала | 689 |