
Презентация "Числовая окружность"

Краткое описание документа:
Данный обучающий ресурс посвящен теме «Числовая окружность».
[img]/jpg/Chislovaja_okruzhnost_10.1.jpg/img][img]/jpg/Chislovaja_okruzhnost_10.2.jpg[/img]
На первом слайде приводятся три общих видов функций в форме уравнений. Первая – это степенная функция, вторая – линейная, третья – иррациональная.

После этого приводятся тригонометрические функции синуса, косинуса, тангенса и котангенса. На третьем слайде мы видим иллюстрацию окружности на координатной оси.
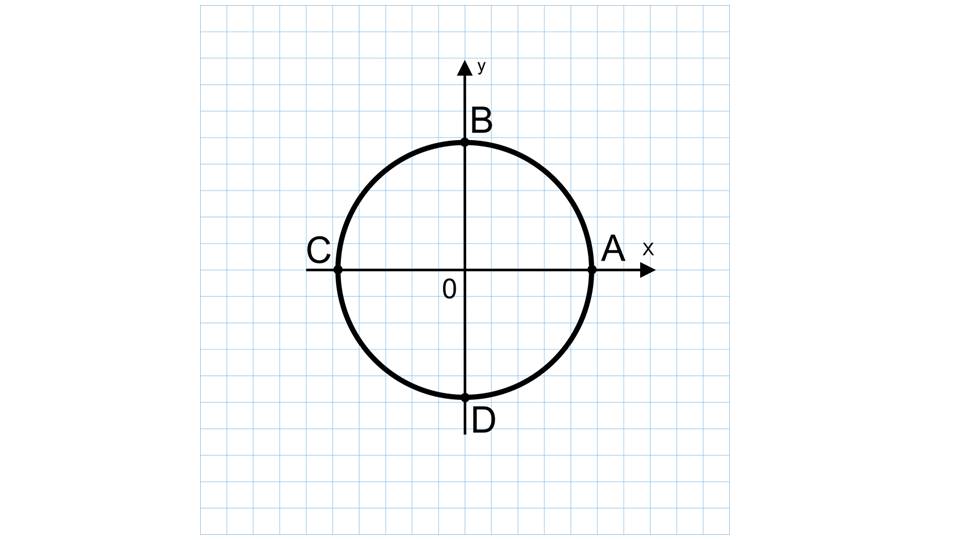
Центром окружности является точка (0, 0) , а точки A, B, C, Dявляются точками пересечения окружности с осями координат. Далее дается некоторое замечание. Если не указана единица измерения окружности, то она условно считается единичной. Радиус такой окружности же условно считается равной 1.
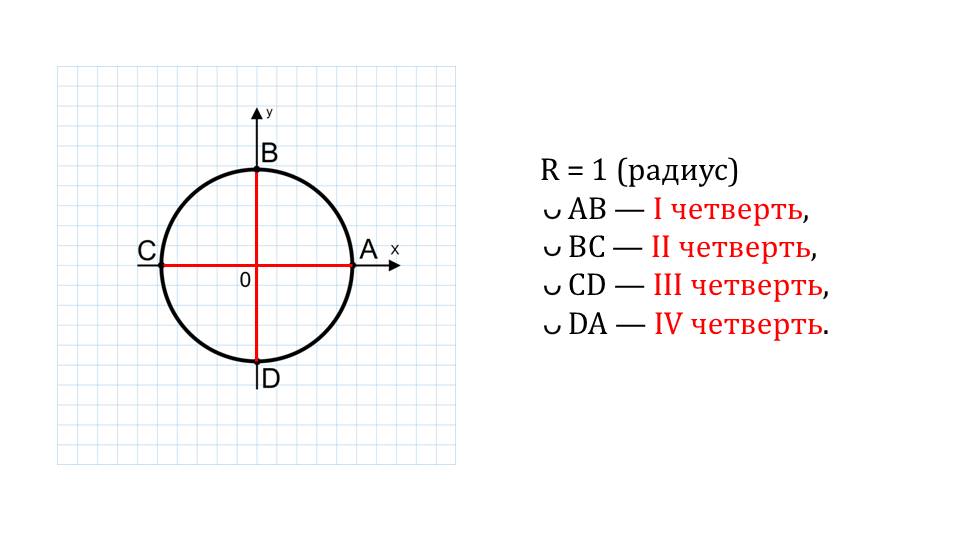
На следующем слайде приводится обозначение дуги. Мы видим, что на каждой четверти координатной плоскости мы видим определенную дугу, например, дуга AB.

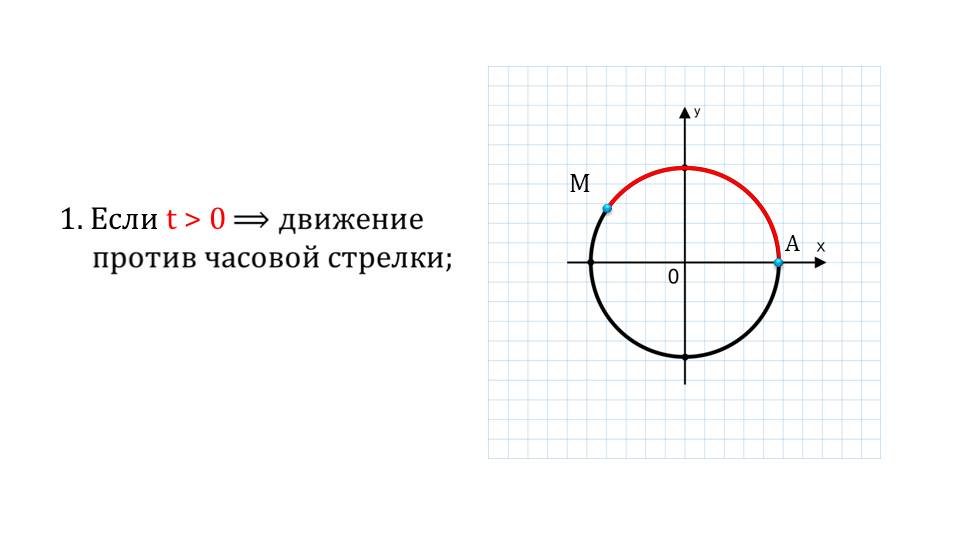
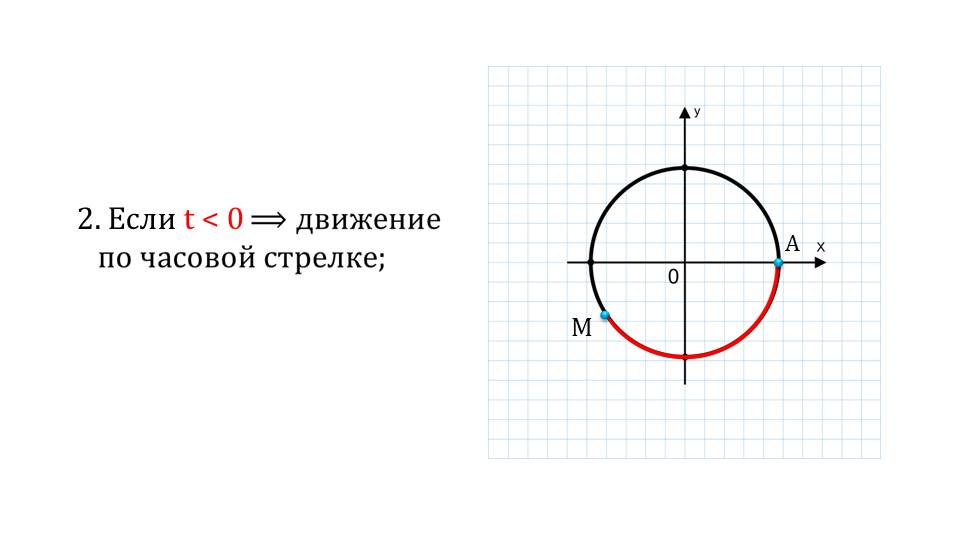
Далее рассматривается движение точки по и против часовой стрелке по окружности. Единичная окружность будет называться числовой, если установлены соответствия между ее точками и действительными числовыми значениями.


Стоит вспомнить некоторые геометрические характеристики окружности, которые ранее были пройдены. Длина окружности обозначается через латинскую букву l. Для того чтобы найти длину окружности необходимо посчитать произведение радиуса, умноженное на 2 и число Пи.
Радиус окружности обозначается через заглавную латинскую букву R. Так как радиус единичной окружности равняется 1, то для нахождения длины такой окружности достаточно умножить Пи на число 2. Таким образом, длина единичной окружности примерно будет равняться 6,28.
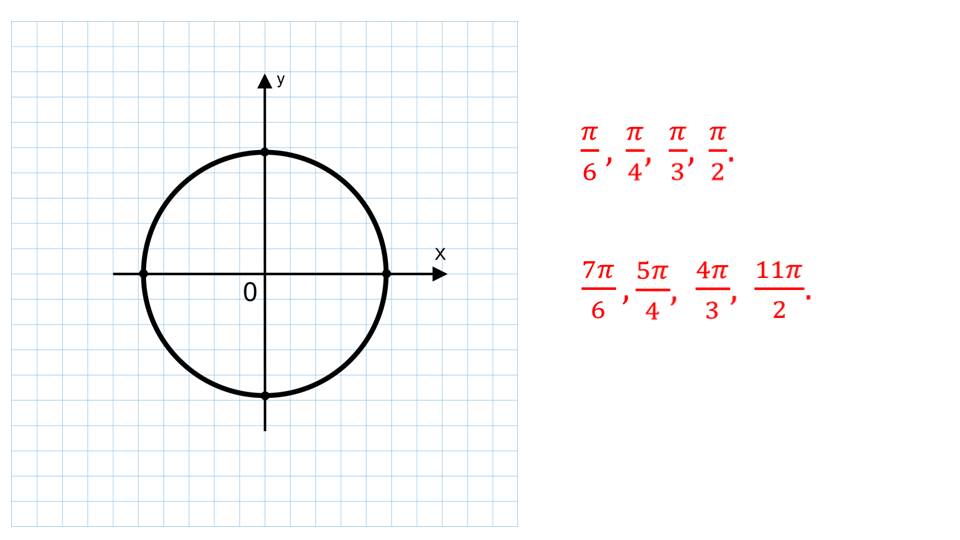
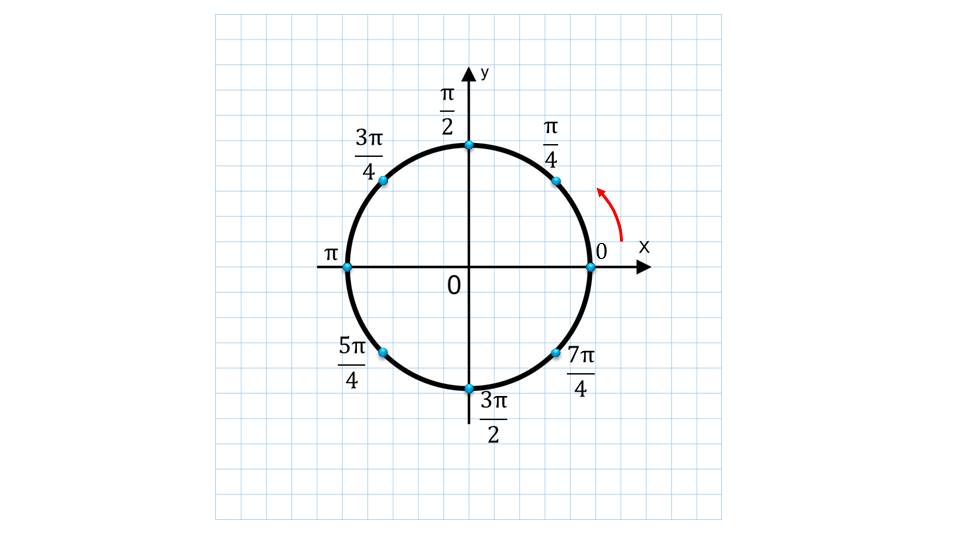
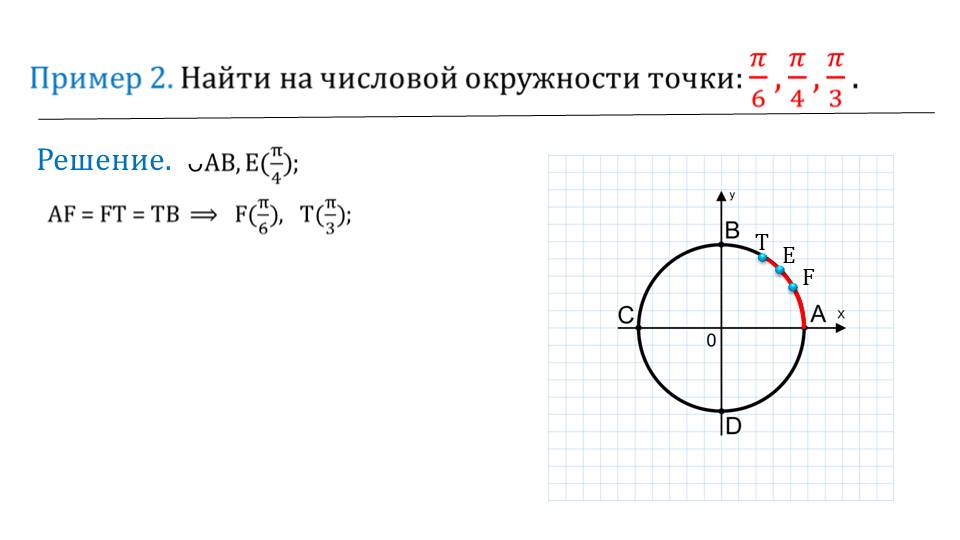
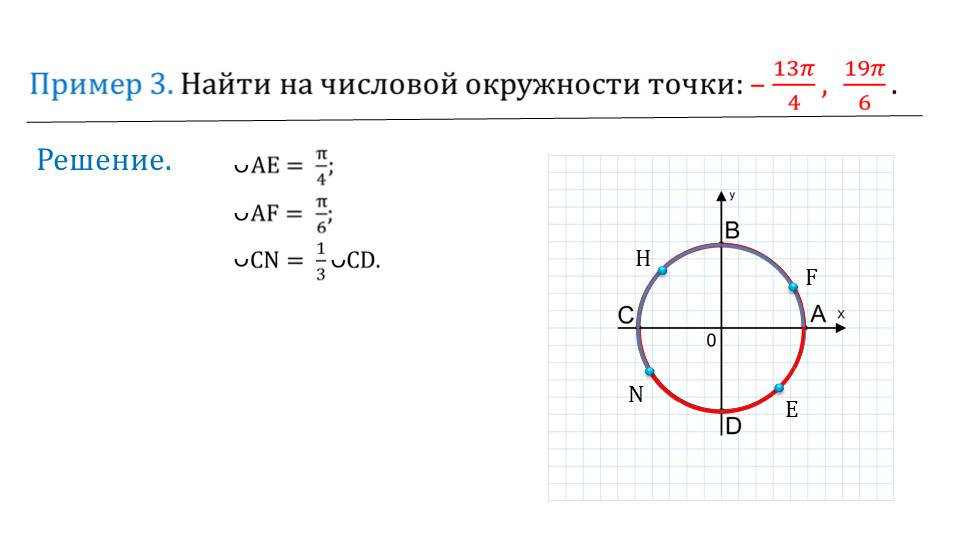
Далее приводятся пример, на которых необходимо найти заданные точки на окружности. Это важно знать при дальнейшем изучении тригонометрии.
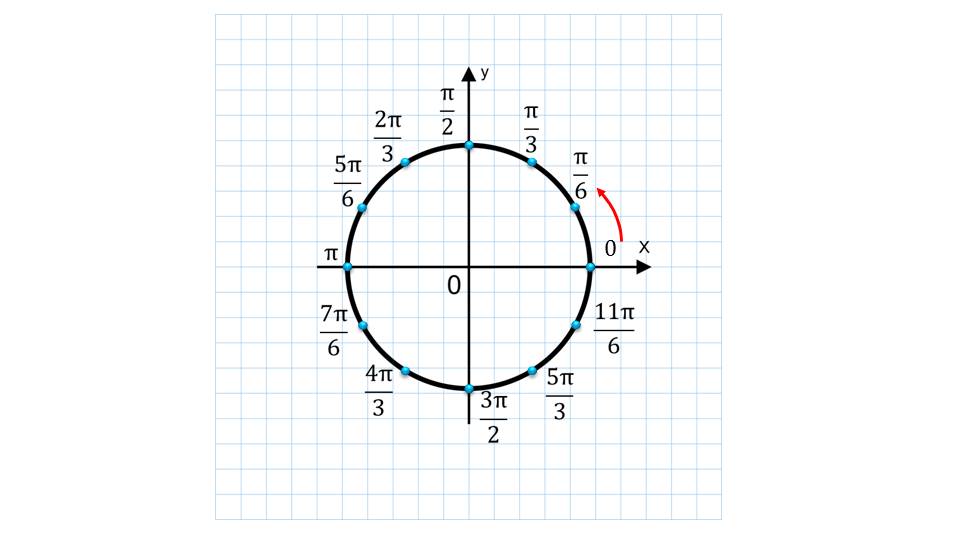
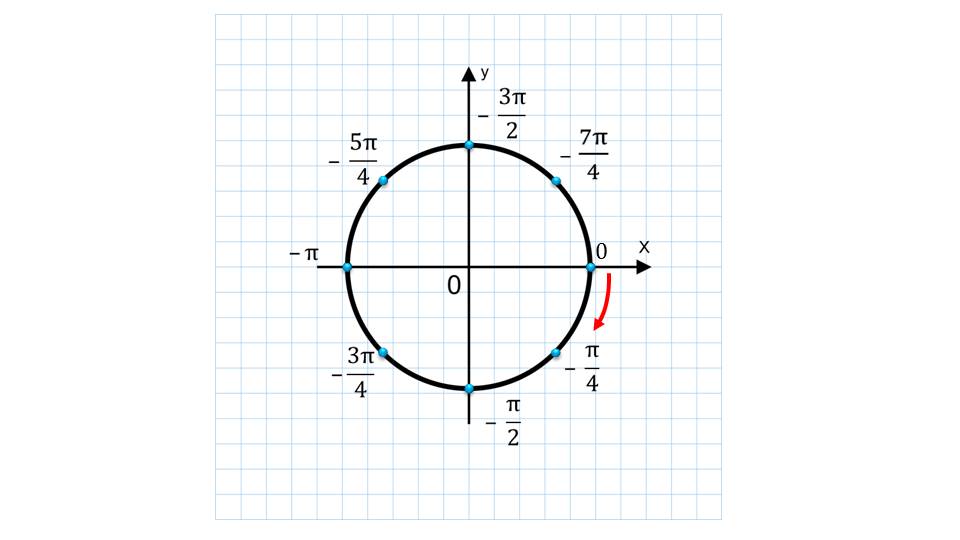
Также указывается понятие о периодичности. С данным термином школьники столкнутся ближе в последующих уроках.


Данная презентация поможет молодому учителю провести интересный урок, как обычный, так и открытый.

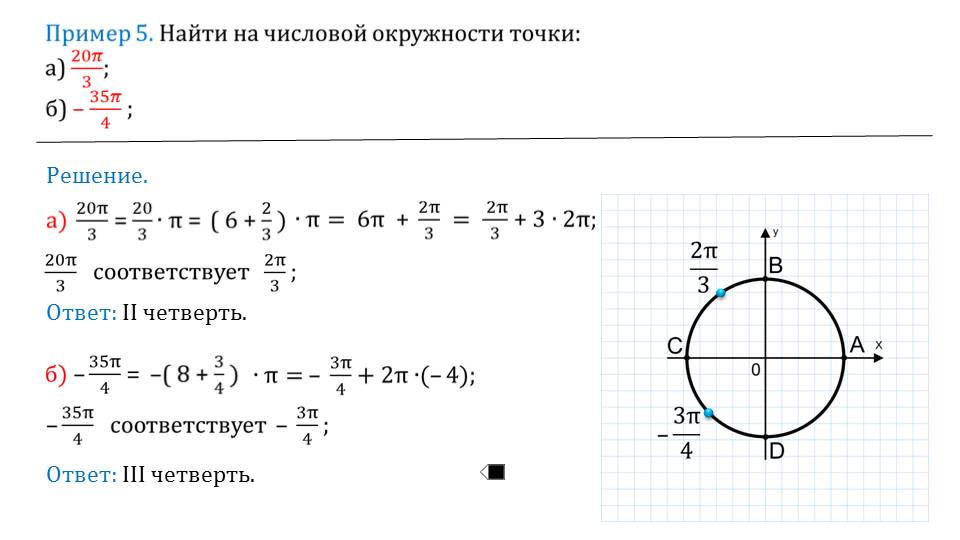
Школьники будут концентрированы на теме благодаря понятным иллюстрациям.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5905 |
| Номер материала | 783 |