
Презентация "Числовая окружность на координатной плоскости"

Краткое описание документа:
Данная презентация поможет десятиклассникам при изучении одной из тем касательно числовой окружности.
Речь идет о рассмотрении числовой окружности на координатной плоскости.
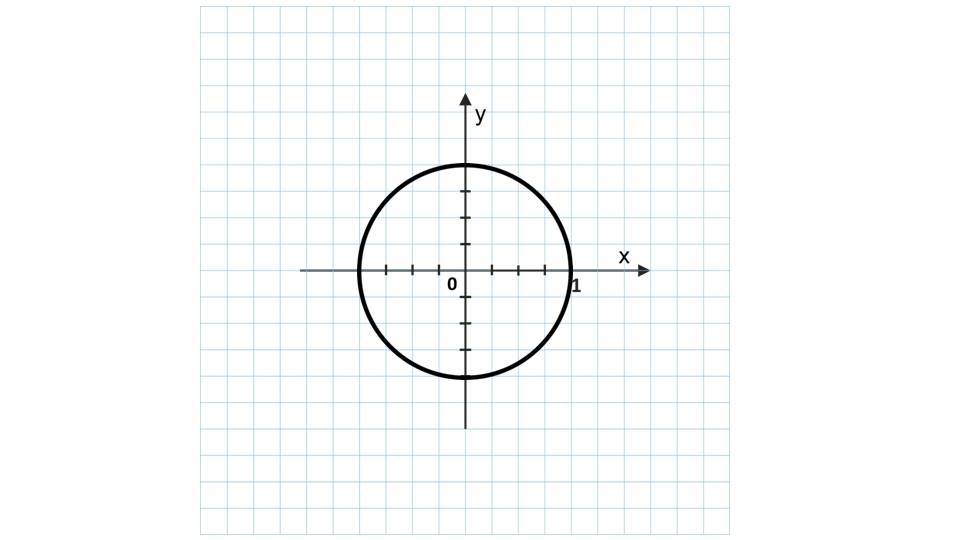
На первом слайде демонстрируется координатная плоскость, на которой изображается окружность. Мы видим, что центр окружности в начале координат, а радиус равняет единице. Это говорит о том, что данная окружность является единичной.
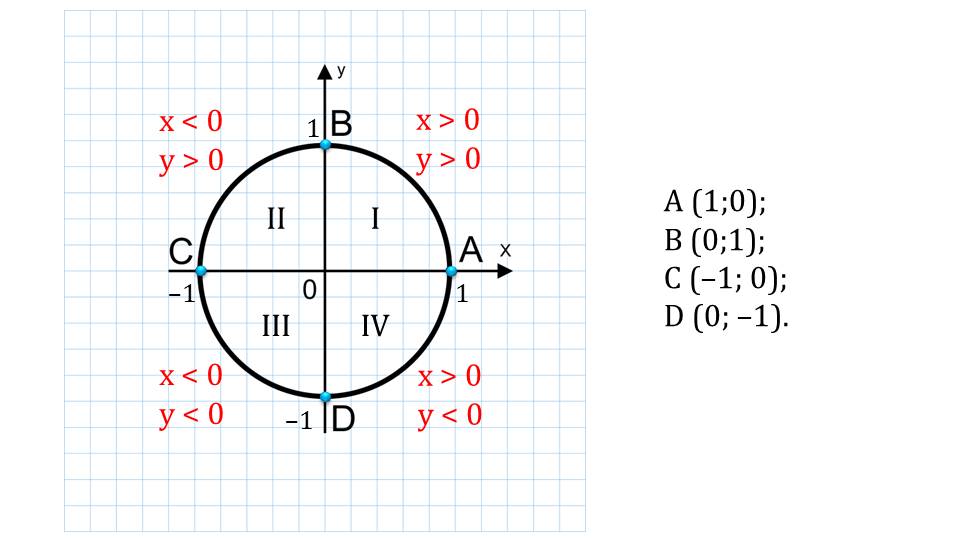
Следующий слайд демонстрирует этот же рисунок, с более подробным его описанием. Мы видим, что обозначены точки пересечения окружности с осями координат, которые разбивают ее на 4 дуги. Также обозначены четверти римскими цифрами, как это принято в большинстве источников.


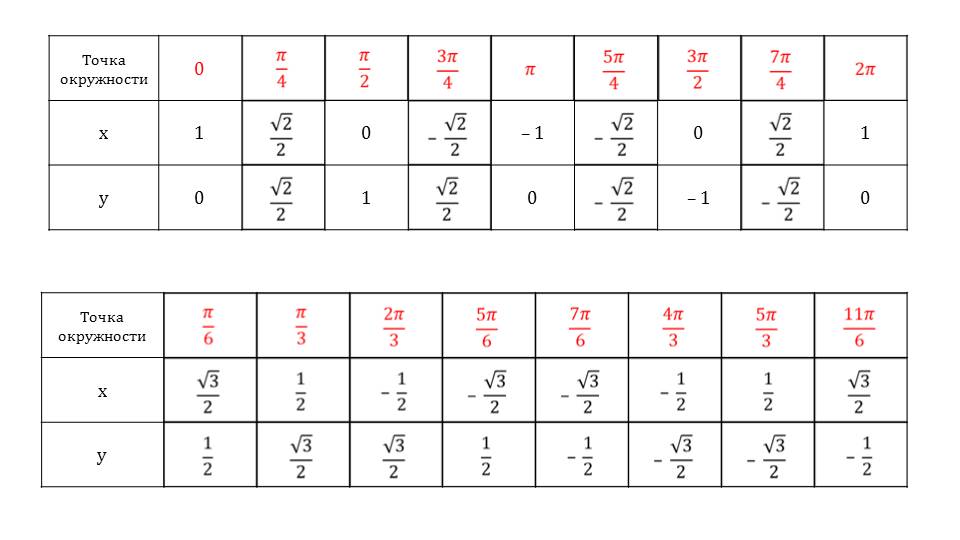
С правой стороны от рисунка показаны координаты каждой точки пересечения окружности с осями ОХ и ОУ. Также расписаны значения х-ов и у-ов на той или иной четверти.
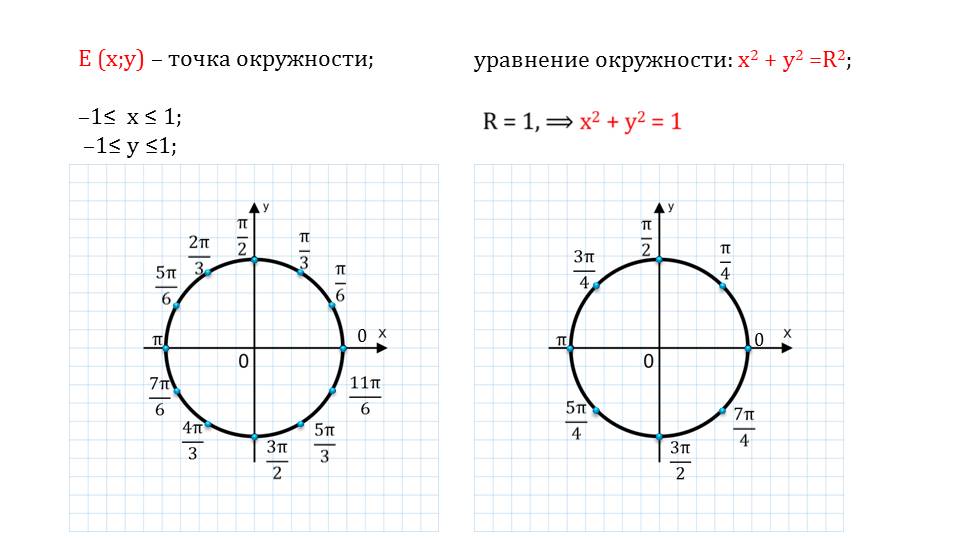
На следующем слайде приводится общий вид обозначения произвольной точки на окружности. Приводит функция, построив которую мы получим окружность. С правой стороны уравнения данной функции стоит радиус ее в окружности. Мы ведь знаем, чему равняется радиус единичной окружности – единице.

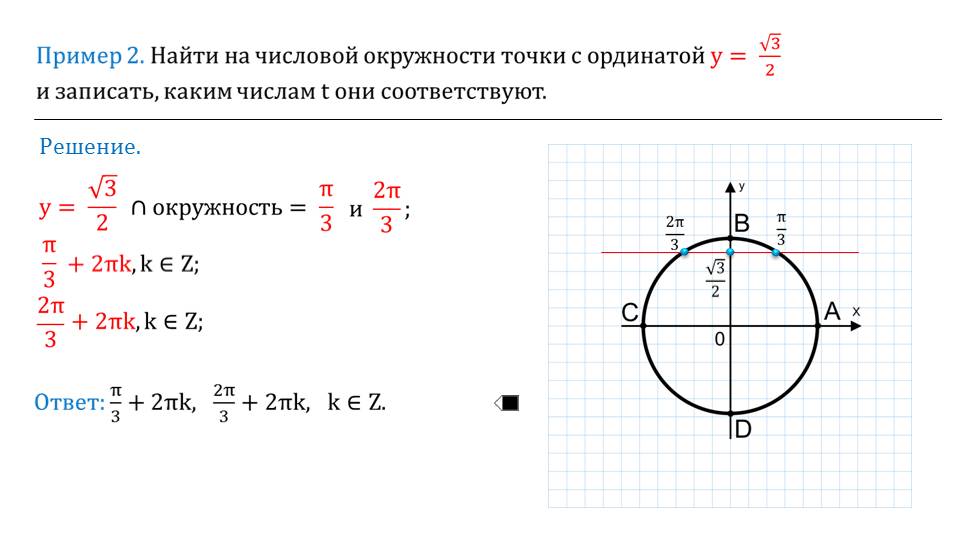
Подставив данное значение, мы и получим уравнение единичной окружности. С левой стороны на данном слайде можно увидеть, что отмечается очень важный и очевидный факт: х-ы и у-ы ограничены интервалом [-1; 1].
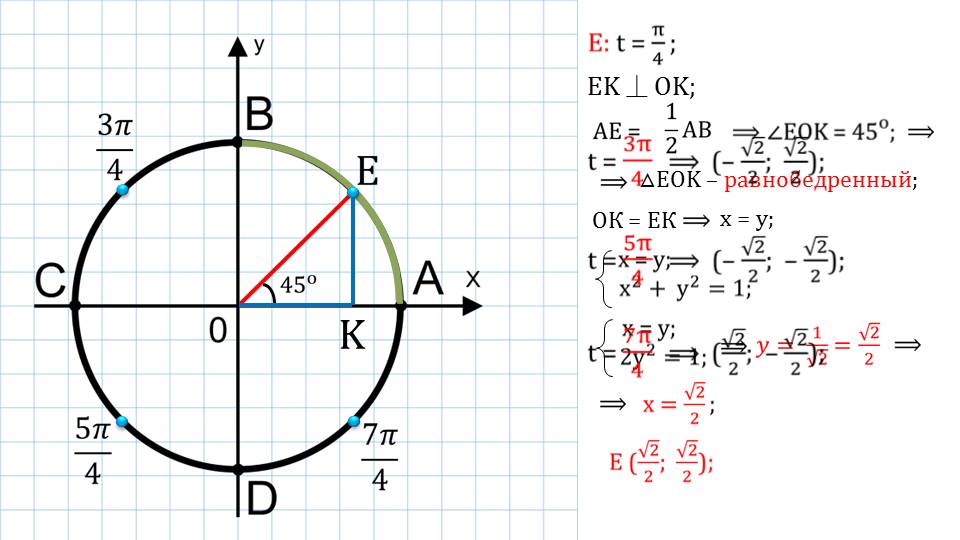
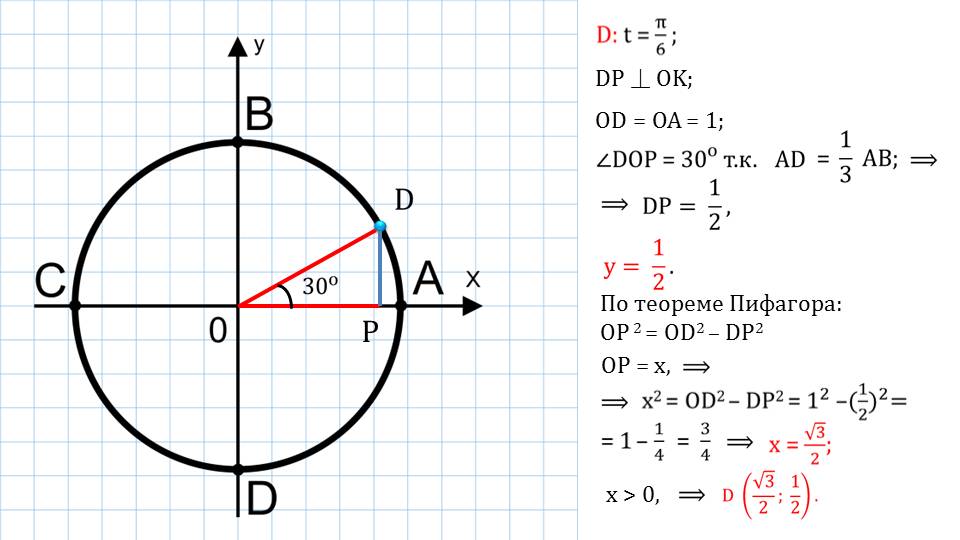
Если выбрать любую точку на окружности, то можно построить прямоугольный треугольник.
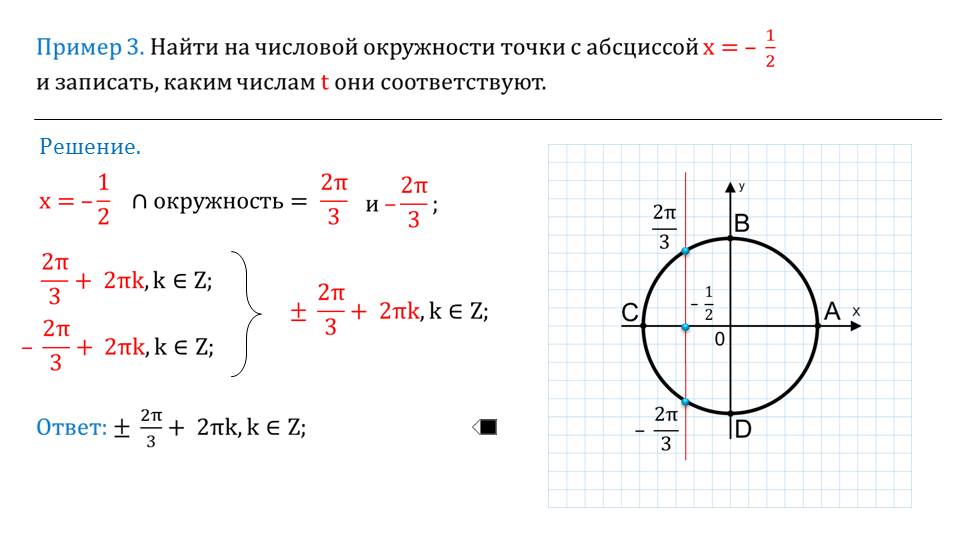
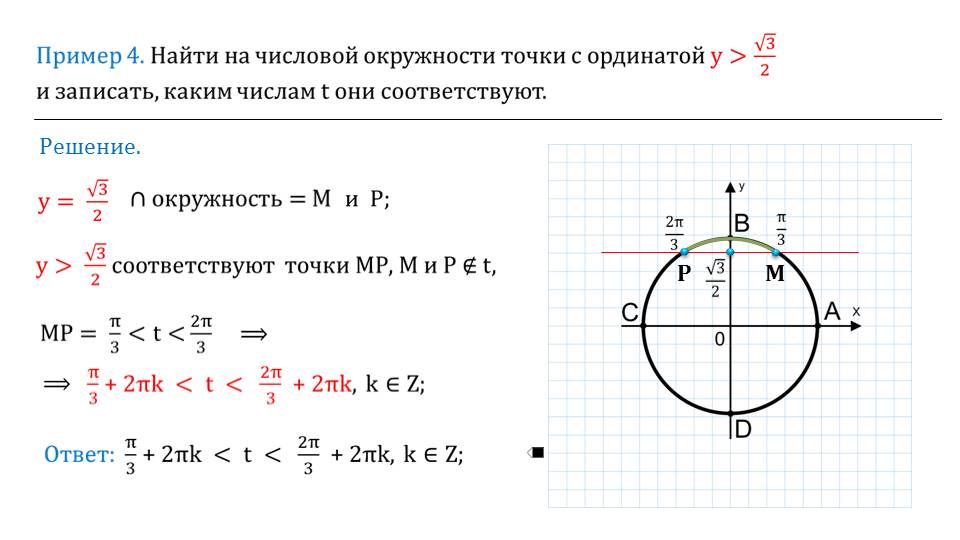
Для этого необходимо соединить две точки – выбранную точку на окружности и началом координат. Третью точку можно получить при проведении от выбранной точки к оси ОХ перпендикуляр.

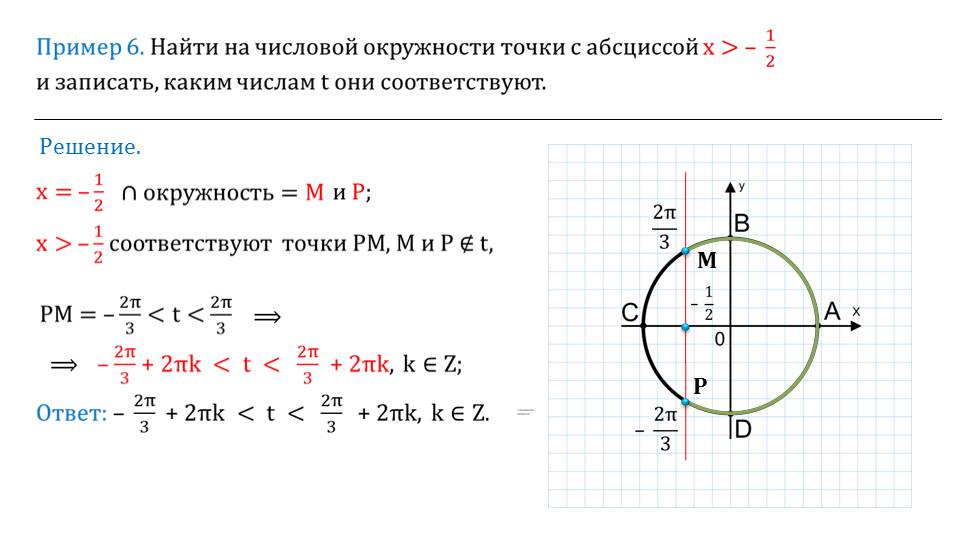
Подробным образом демонстрируется, как с использованием значения угла и знания о дуге окружности можно найти координаты той или иной точки на окружности.
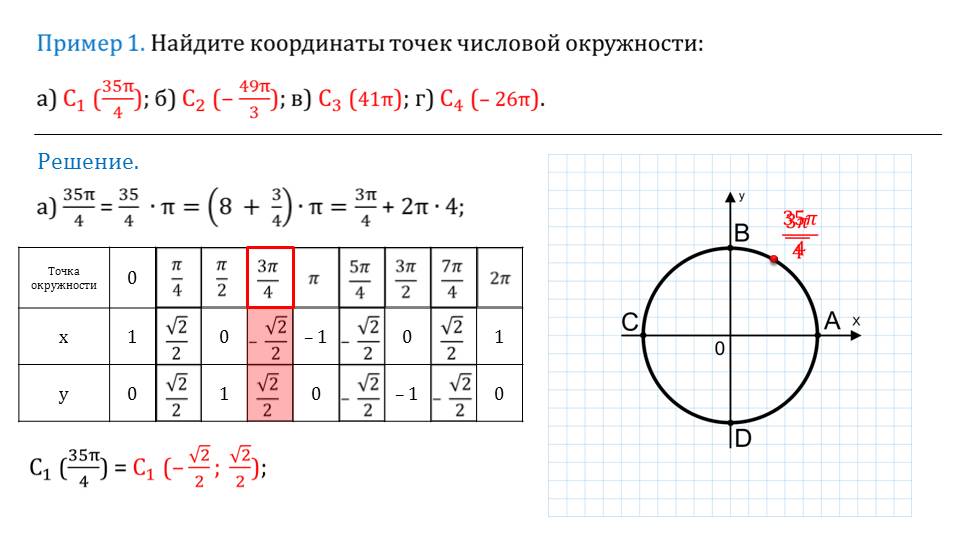
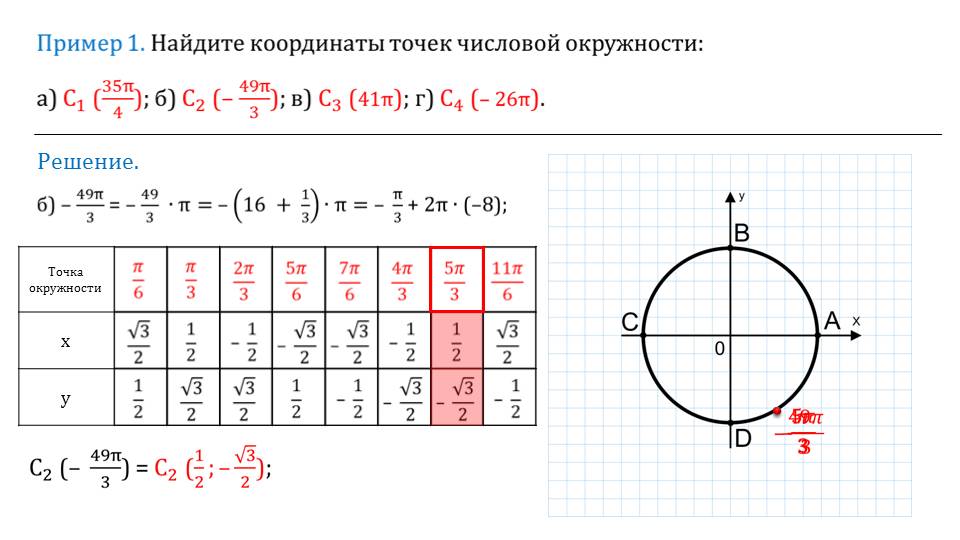
Приводится таблица, с готовыми расчетами, которую можно использовать при решении различных задач. Чтобы правильно ею пользоваться, рассматриваются примеры.
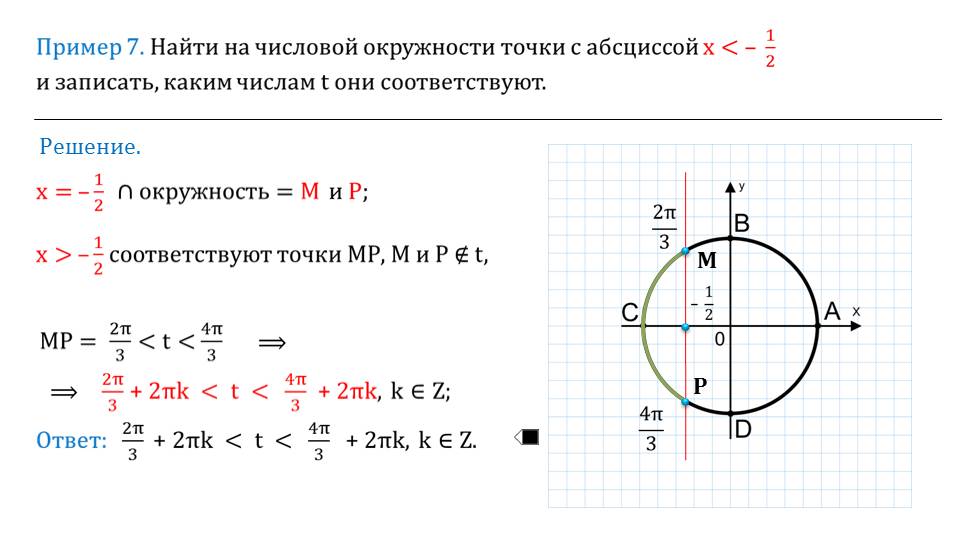
Их можно предложить решить 10-классникам самостоятельно. Будет полезным также их рассмотрение в классе с учителем или индивидуально с репетитором.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 9850 |
| Номер материала | 785 |