
Презентация "Формула Ньютона-Лейбница. Нахождение площадей плоских фигур с помощью интеграла"

Краткое описание документа:
В данной презентации по алгебре для 11-го класса рассмотрим определенный интеграл, свойства определенного интеграла, формулу Ньютона-Лейбница, узнаем, как можно находить площади плоских фигур. В начале презентации автор дает определение, с которым учащиеся ознакомились в предыдущей теме: определенным интегралом от функции на интервале от a до bназывается предел суммы слагаемых, количество которых неограниченно возрастает, если каждое из этих слагаемых стремится к нулю. Нижний предел интегрирования обычно обозначают как «a», верхний предел интегрирования – как «b».


Рассмотрим теорему. Если на интервале от aдо bфункция y = f (x) является непрерывной, то интеграл от функции f (x) на промежутке от aдо b по dxможно вычислить как разницу первообразных от функций f (a) и f (b). Данное равенство называется формулой Ньютона-Лейбница.
Дается пример. Необходимо вычислить интеграл. При решении находится первообразная для x3. Применяя формулу Ньютона-Лейбница, можно вычислить значение интеграла.
Далее в презентации записаны свойства, которыми характеризуется определенный интеграл:
1) интеграл суммы двух функций от aдо b по dxравен сумме интегралов первой функции от aдо bпо dx и второй функции от aдо bпо dx;
2) постоянный множитель может быть вынесен за знак определенного интеграла;
3) если на промежутке от aдо b есть точка с, то определенный интеграл функции на отрезке от aдо bпо dxравен сумме интегралов функции на отрезке от aдо с по dx и функции на отрезке от с до bпо dx.


Рассмотрим пример 2. Вычислить интеграл на интервале от –2 до 4 по dx. При решении преобразуем исходное выражение, используя первое свойство, записывая интеграл функции как сумму интегралов функций. Вынесем постоянные множители за скобки. Найдем первообразную функции. Найдем значение каждого интеграла, применяя формулу Ньютона-Лейбница. Вычислим значение исходного интеграла.
Применяя определенный интеграл, можно находить площади плоских фигур. Рассмотрим слайд 6. Если фигура ограничена прямыми x = a, x = b и графиками функций y = f (x), y = g(x), которые являются непрерывными на отрезке от aдо bи таких, что g(x) ≤ f (x) для всех xиз отрезка от aдо b, то площадь фигуры вычисляется по формуле интеграла разности функций f (x) и g(x) от aдо bпо dx.


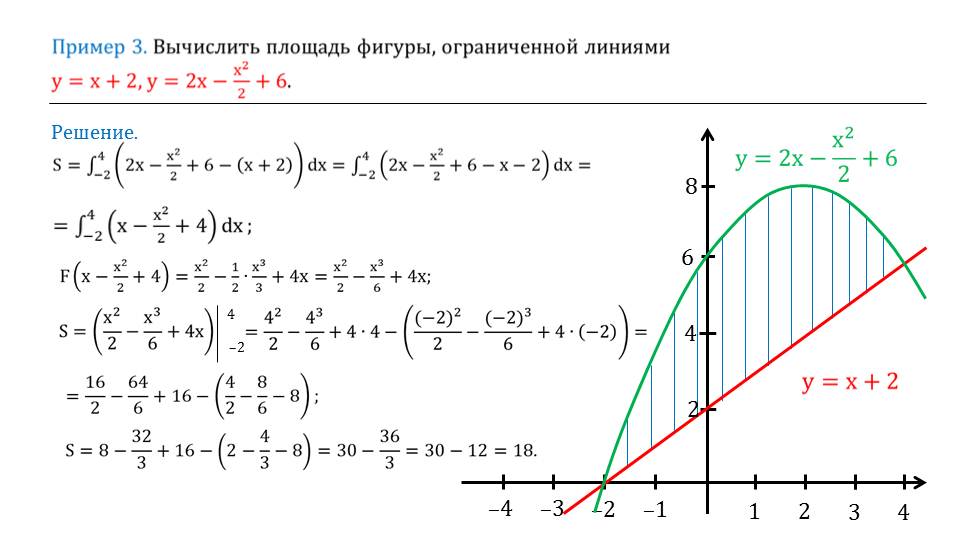
Разберем пример вычисления площади фигуры, которая ограничена линиями y = x + 2, y = 2x – x2/2+ 6. Сделаем схематическое изображение графиков функций. Запишем площадь фигуры S, которая равна интегралу разности функций 2x – x2/2+ 6 и x + 2 от –2 до 4 по dx. Преобразовывая подынтегральное выражение, получим x – x2/2 + 4. Найдем первообразную F (x – x2/2 + 4) = x2/2 – x3/6 + 4x. Применяя для нахождения площади формулу Ньютона-Лейбница, вычислим S = 18.
Итак, из презентации учащиеся узнали свойства определенного интеграла и применение их на практике, изучили формулу Ньютона-Лейбница и научились вычислять площади плоских фигур. Решение примеров, приведенных в презентации, помогает хорошо усвоить и закрепить пройденный материал. Учитель может на свое усмотрение добавить другие примеры в данную тему.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5309 |
| Номер материала | 1038 |