
Презентация «Формула суммы первых n членов арифметической прогрессии»

Краткое описание документа:
Данная презентация разработана автором для использования ее на уроках алгебры в 9 классе, когда изучаются последовательности. Взяв за основу урока данную презентацию, учителю не придется долго готовиться к занятию. Автор все сделал заранее.

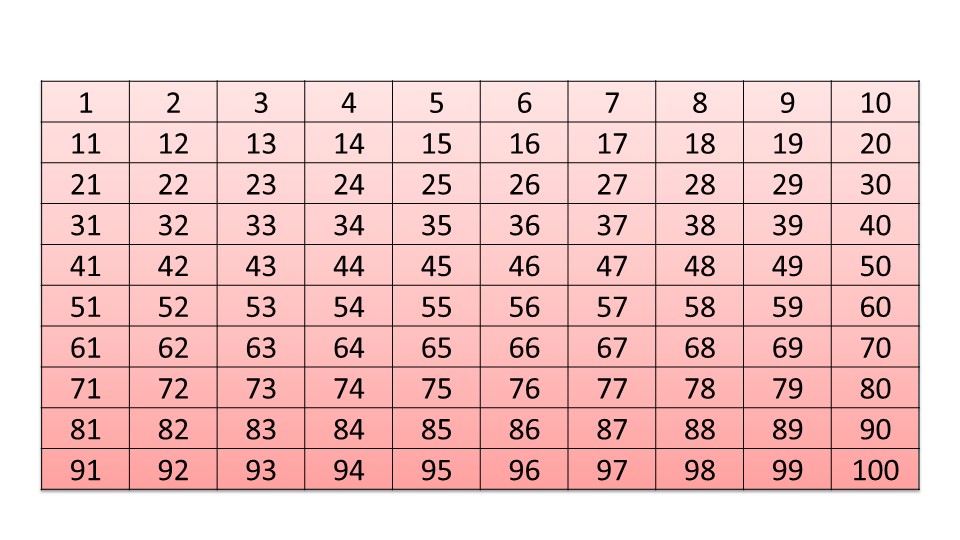
Презентация начинается с того, что предлагается таблица, состоящая из 10 строк и столбцов с пронумерованными ячейками слева направо и сверху вниз. То есть, дана некоторая последовательность, состоящая из 100 членов. На следующем слайде показано, как вычислить сумму всех членной этой последовательности. Используя интересный прием, автор презентации получил довольно просто результат, не складывая всех чисел.
Так как немалый вклад в данную теорию внес знаменитый математик Иоганн Карл Фридрих Гаусс, то его портрет с указанием годов его жизни автор разместил на следующем слайде.
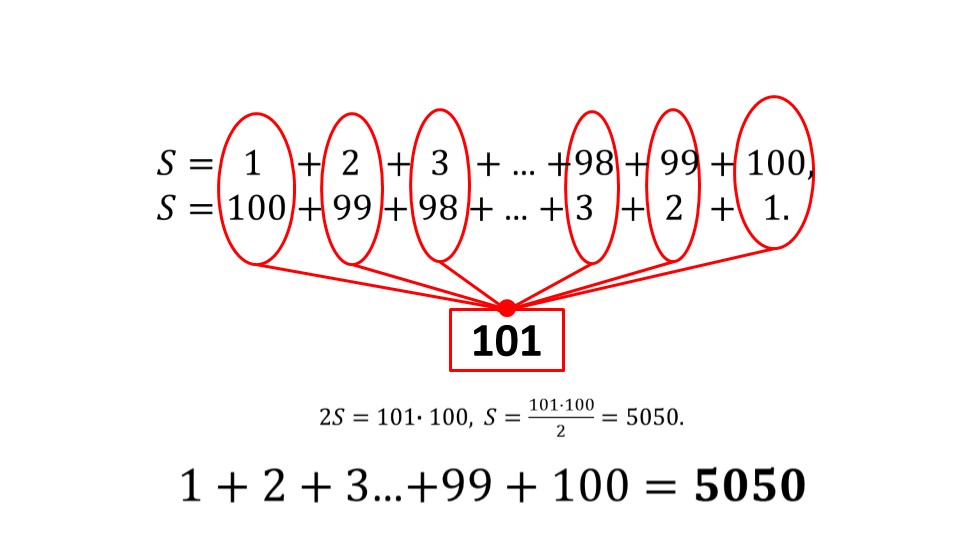

Далее автор показывает, как обозначается сумма первых nчленов арифметической прогрессии. А затем по аналогии с примеров в начале презентации, находится сумма nчленов последовательности в общем виде. Так получается, что при нахождении двойной суммы, можно прийти к одному и тому же выражении. Это автор на следующем слайде и показывает. Он в итоге демонстрирует готовые два варианта формул нахождения суммы nпервых членов арифметической прогрессии. Для первой формулы важно знать 1-й и n-й члены прогрессии и разность, а для второй – достаточно знать 1-й член и разность.
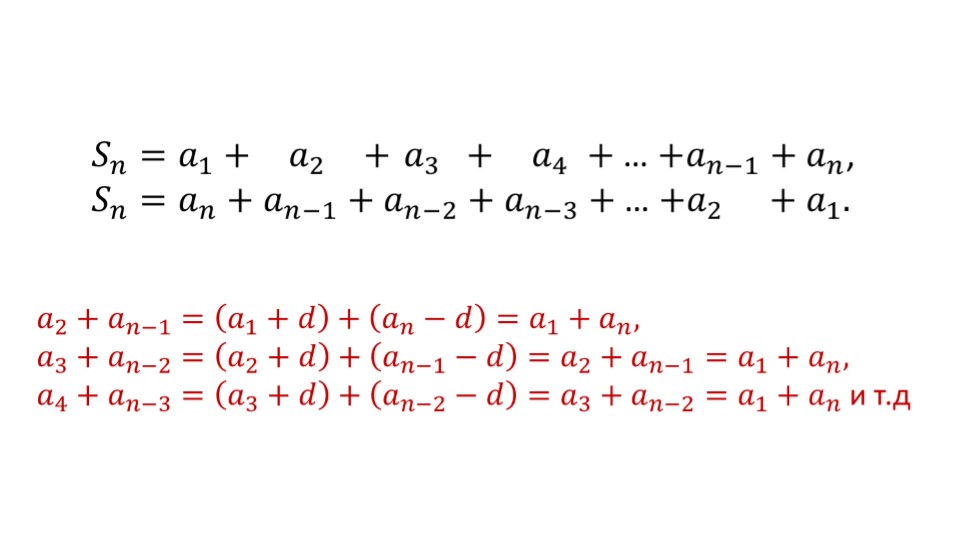
Далее рассматривается пример, где автор предлагает найти сумму nчленов арифметической прогрессии двумя способами, чтобы показать, что результат получается один и тот же, а вычисления немного отличаются.


На следующем же слайде продемонстрирован пример, где для нахождения суммы nчленов прогрессии выбрана наиболее удобная формула. Так автор показывает, что при решении задач важно подбирать рациональные способы и приемы.
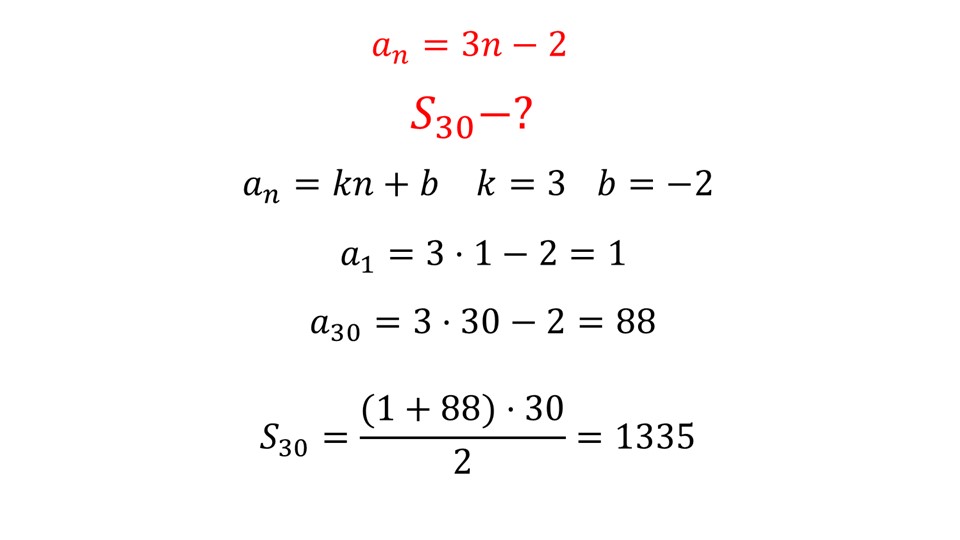

Далее рассматривается пример, который заставляет подумать немного больше обычного. Такие примеры позволяют активизировать мыслительные процессы и заставить обучающихся активно работать на уроке.
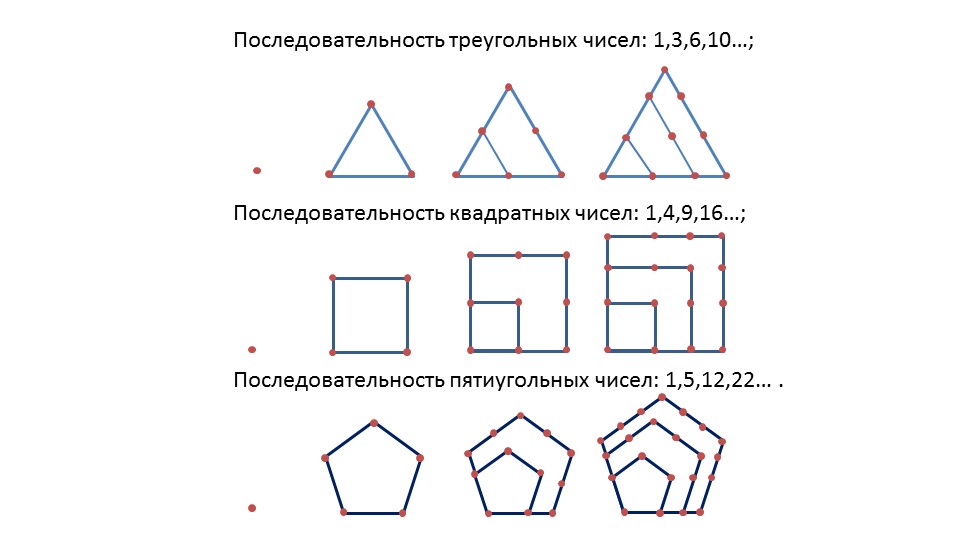
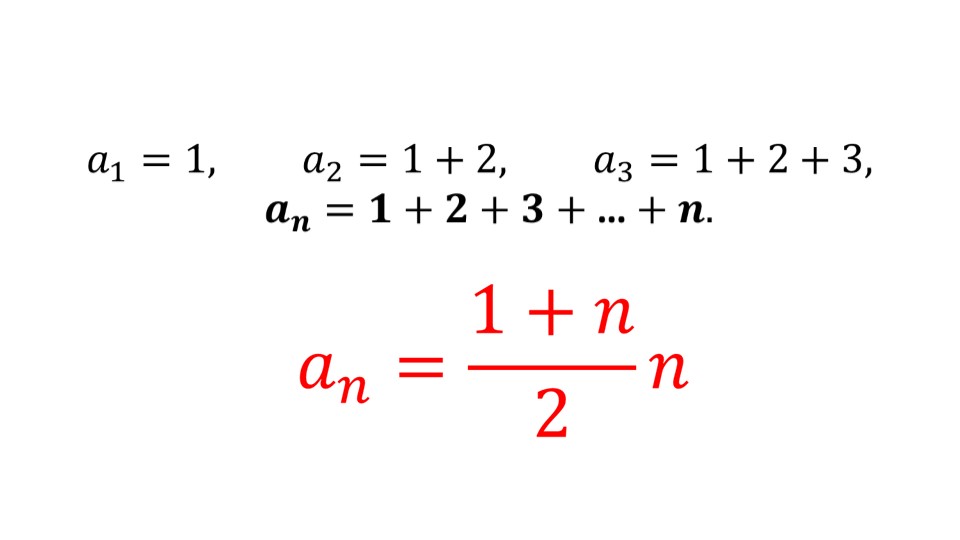
На следующем слайде представлены не менее интересные примеры: здесь изображены рисунки и пояснения к ним. Оказывается, бывают последовательности треугольных, квадратных и пятиугольных чисел. Такие последовательности записаны здесь же. А на следующих трех слайдах идет подробная расшифровка того, как получаются такие последовательности. В итоге на всех трех слайдах автор выделил итоговые формулы n-го члена таких последовательностей.
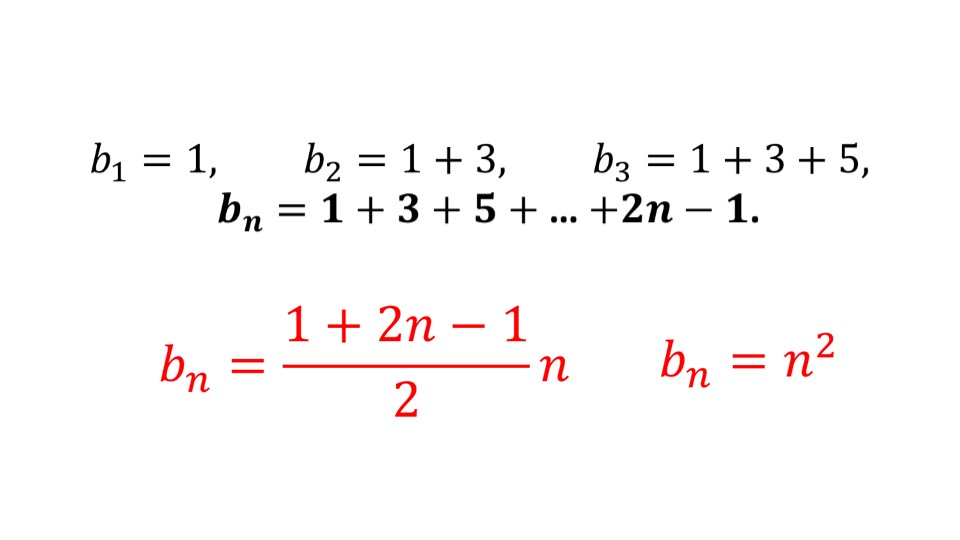
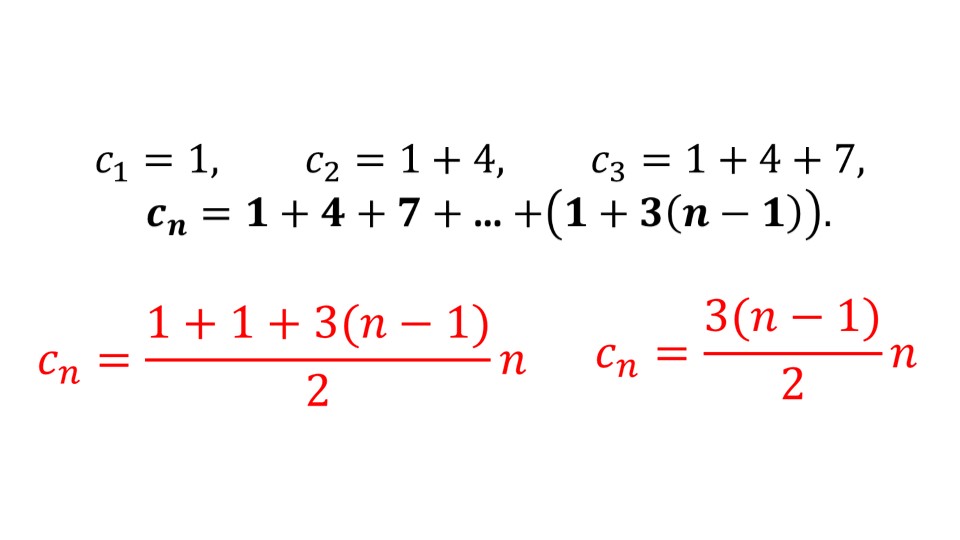
Подобные примеры помогают развивать у обучающихся интерес к учебному предмету математика. Данная презентация также этому способствует.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5506 |
| Номер материала | 638 |