
Презентация "Формулы двойного аргумента"

Краткое описание документа:
Презентация «Формулы двойного аргумента» предназначена для наглядного представления учебного материала по данной теме. В презентации представлены формулы двойного аргумента, описывается их выведение, рассматриваются примеры решения заданий, которые требуют знаний изученных формул. Задача пособия – наглядно, удобно для ученика представить учебный материал, сопровождающий объяснение учителя, способствовать запоминанию формул, формировать умение решать задания, применяя изученные формулы. На экране хорошо видны представленные формулы, они выделены для лучшего их запоминания, разбираемые примеры дополняются необходимыми таблицами значений, материал подается последовательно, хорошо структурирован.

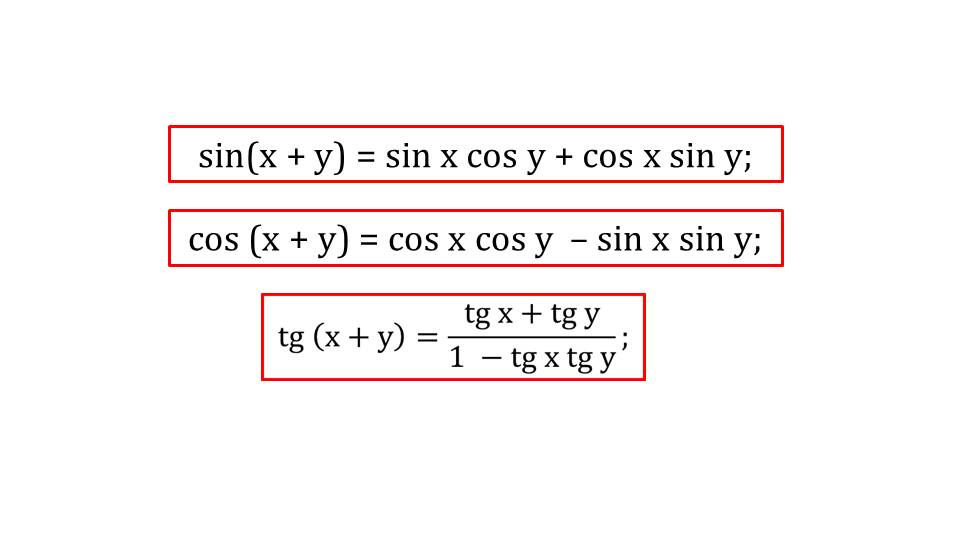
Наглядности и удобства материала для усвоения удается достичь при помощи способов, которые применяются в демонстрации презентации. Использование анимационных эффектов позволяет структурировать информацию, отображать ход рассуждения при решении задач. Описания дополняются таблицами значений, выделением цветом, при помощи которых ученикам легче освоить методы решения, обнаружить особенности данного задания, запомнить формулы.
Презентация начинается с определения формул двойного аргумента. На слайде отображается, что формулами двойного аргумента называются формулы для выражения sin 2x, cos 2x, tg 2x через sin x, cos x, tg x.
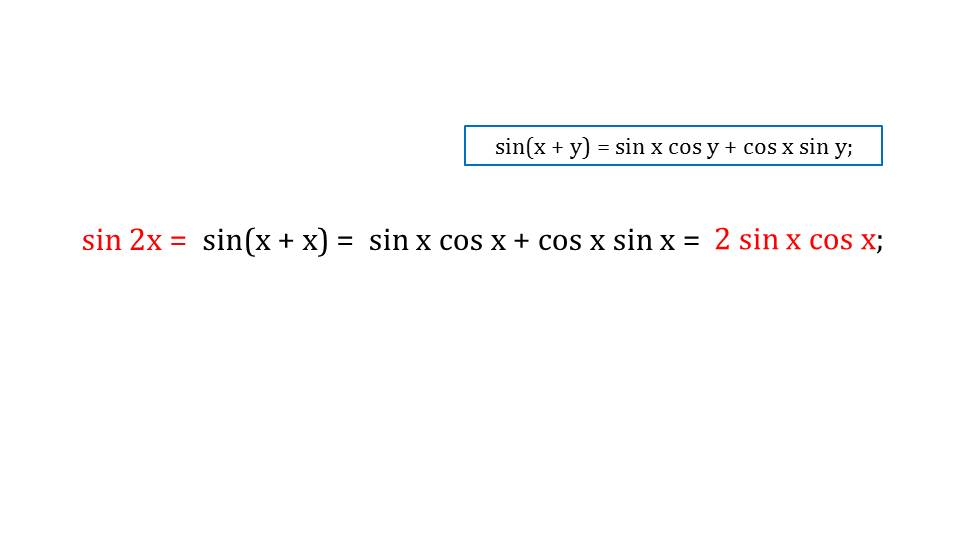

Прежде чем вывести формулы двойного аргумента, ученикам напоминаются формулы, изученные на предыдущих уроках – разложение в виде суммы или разности произведений синуса суммы аргументов, косинуса и тангенса суммы аргументов. На слайде 3 отображается выведение формулы синуса двойного аргумента. Для выведения формулы используется формула суммы двух аргументов. Если представить двойной аргумент как сумму двух одинаковых аргументов из формулы синуса суммы выходит формула двойного аргумента sin 2x=2sin x cos x.

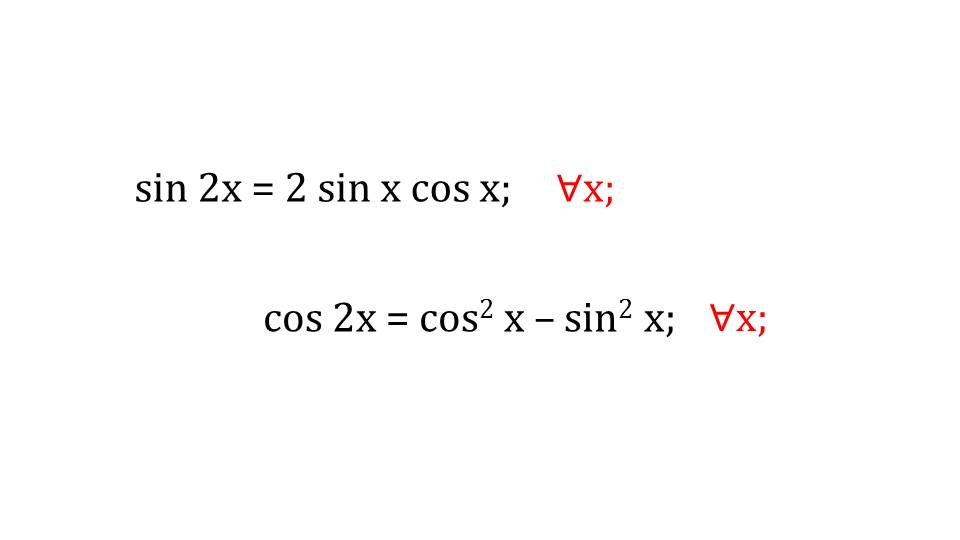
На слайде 4 формула преобразования косинуса двойного угла выводится из формулы косинуса суммы аргументов. Если двойной аргумент представить суммой двух одинаковых аргументов и подставить их в формулу косинуса суммы аргументов, получаем выражение для нахождения косинуса двойного аргумента cos 2x=cos2 x-sin2 x.
Слайд 5 описывает выведение формулы тангенса двойного угла из формулы тангенса суммы аргументов. На экране отображается формула тангенса суммы аргументов. Двойной аргумент представляется в виде суммы двух одинаковых аргументов. После подстановки двойного аргумента в формулу тангенса суммы получаем формулу для определения тангенса двойного угла tg 2x=2 tg x/(1-tg2 x).
На шестом слайде отмечается, что формула для нахождения синуса двойного угла sin 2x=2 sin x cos x и формула для нахождения косинуса двойного угла cos 2x=cos2 x-sin2 x будут справедливы для любого значения х. Также демонстрируются ограничения формулы для нахождения тангенса двойного угла tg 2x=2 tg x/(1-tg2 x).
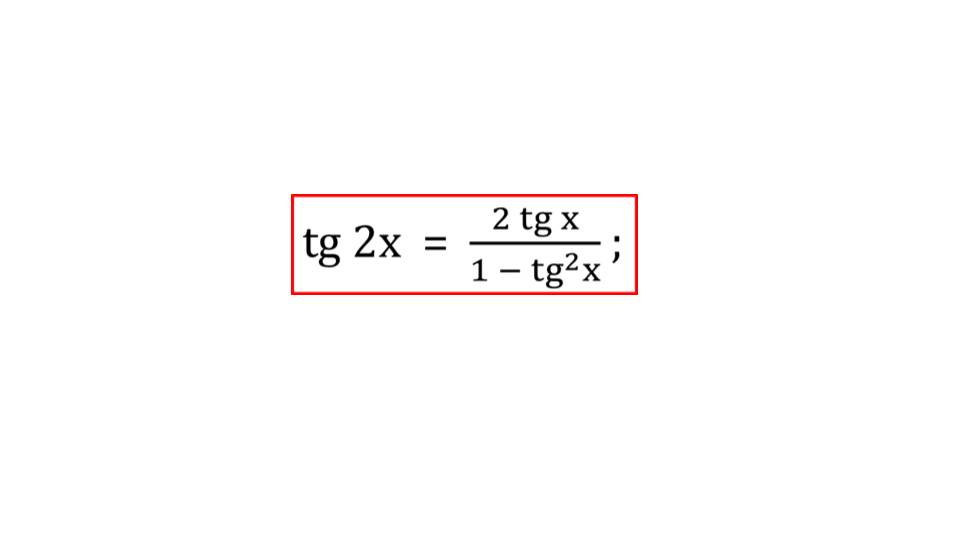

На слайде 8 описывается решение задания, в котором необходимо сократить дробь cos 2x/(1-sin 2x). В правую часть экрана выводятся формулы, знание которых поможет произвести необходимые сокращения. Продемонстрировано, что если в знаменателе дроби 1 представить как сумму квадрата синуса и квадрата косинуса, а для представления sin 2x применить формулу двойного аргумента, то знаменатель представляет собой квадрат разности косинуса и синуса аргумента х. После преобразования cos 2x с помощью формулы двойного аргумента получается разность квадратов тригонометрических функций, которая может быть представлена в виде произведения суммы и разности (по формуле сокращенного умножения). Получив произведения в числителе и знаменателе дроби, можно сократить одинаковые множители. После сокращения дробь принимает вид (cos x + sin x)/(cos x – sin x).
В примере 2 необходимо доказать тождество cos 2x=(1-tg2 x)/(1+tg2 x). Чтобы доказать тождество, необходимо вспомнить формулы, знание которых может пригодиться в решении задачи. В правой части экрана отображается основное тригонометрическое тождество, которое поможет сделать полезные преобразования. Сначала в дроби тангенс представляется как отношение синуса к косинусу аргумента. Затем одинаковые множители в дробях сокращаются. После сокращений остается выражение cos2 x-sin2 x, которое представляет собой cos 2x.


На слайде 10 описывается решение примера, в котором вычисляется значение выражения sin75°sin15°. Аргумент 15° может быть представлено разностью аргументов sin(90°-75°). Используя формулу sin(π/2+x)=cos x, приводим выражение к виду sin75°cos75°. Зная формулу синуса двойного угла отмечаем, что данное выражение можно записать в виде sin 2·75°/2=sin 150°/2. Пользуясь формулами приведения, данное выражение представляем в виде cos 60°/2. После подстановки значения косинуса получаем значение выражения ¼. Таким образом, значение выражения sin75°sin15°=1/4.
На последнем слайде рассматривается решение уравнения sin6x+cos3x=0. Очевидно, sin6x может быть разложен по формуле двойного аргумента, представив 6х=2*3х. После применения формулы уравнение получает вид 2sin3xcos3x+cos3x=0. После вынесения за скобки общего множителя cos3x получаем уравнение cos3x (2sin3x+1) =0. Равенство будет справедливым тогда, когда хотя бы один из множителей будет равен нулю. Решение сводится к поиску решений двух уравнений cos 3x=0, 2sin 3x+1=0. Решение первого уравнения ищем из формулы 3х=π/2+πn для любого целого n. Отсюда х=π/6+πn/3. Решив второе уравнение, получаем x=(-1)n+1·n/18+πn/3 для любого целого n. Таким образом, решение уравнения состоит из двух частей: х= х=π/6+πn/3 и x=(-1)n+1·n/18+πn/3.

Презентация «Формулы двойного аргумента» может применяться для повышения эффективности традиционного урока. Также данное пособие станет помощником учителя, преподающего алгебру дистанционного. Детальное объяснение решения задач с использованием изученных формул поможет ученику освоить тему самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5658 |
| Номер материала | 799 |