
Презентация "Функции y = tgx, y = ctgx, их свойства и графики"

Краткое описание документа:
В предыдущих уроках были рассмотрены функции косинуса и синуса. Были изучены их основные свойства и построены графики. Также были рассмотрены их основные преобразования, приведены основные алгоритмы построения графиков данных преобразованных функций.


Пора перейти к изучению функций тангенса и котангенса. Что они с собой представляют, как они определяются и получаются из синуса и косинуса, школьники уже изучили. Для того, чтобы найти тангенс для некоторого значения, необходимо поделить его синус на косинус, а котангенс, наоборот, поделить косинус данного значения на синус.
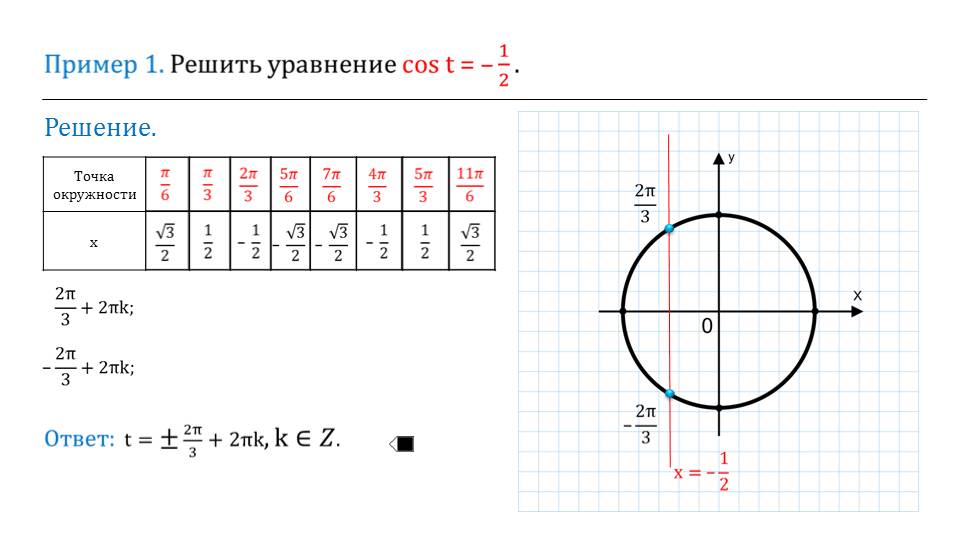
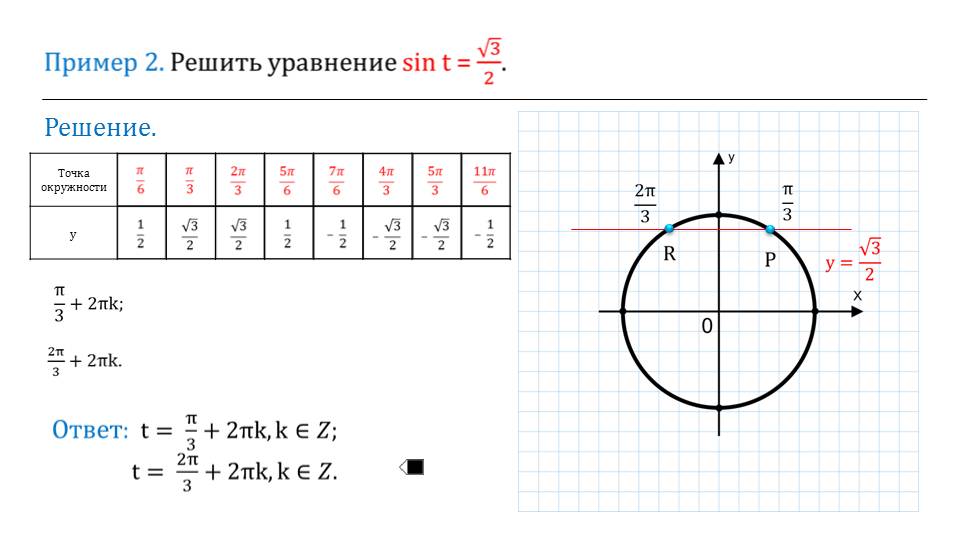
На первом приветственном слайде выводятся функции тангенса и котангенса. Сразу после этого дается первое свойство тангенса. Первое, что необходимо отметить при изучении любой функции – это область определения. Областью определения графика функции тангенса является вся числовая ось, то есть вместо х мы можем поставить все значения, кроме определенных периодичных значений. Они в общем виде выведены на слайде.
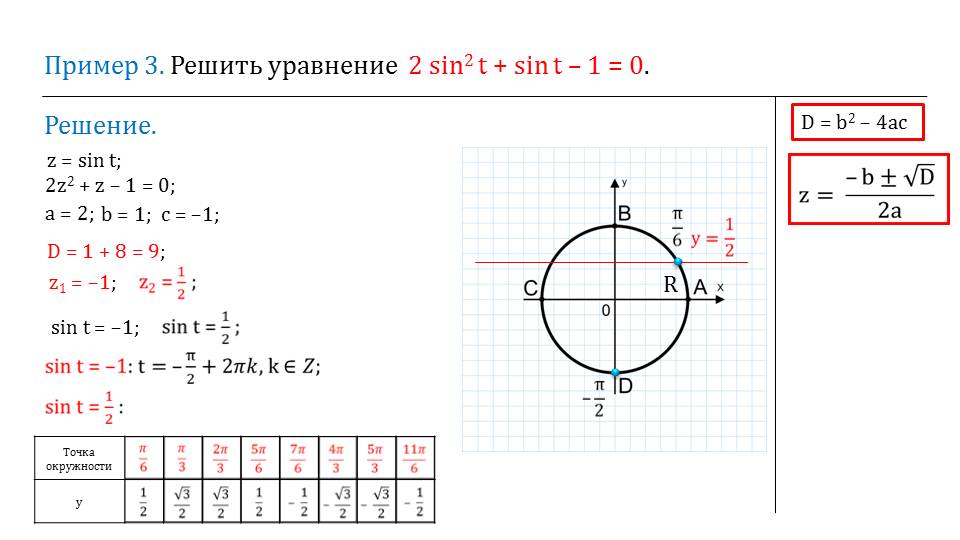
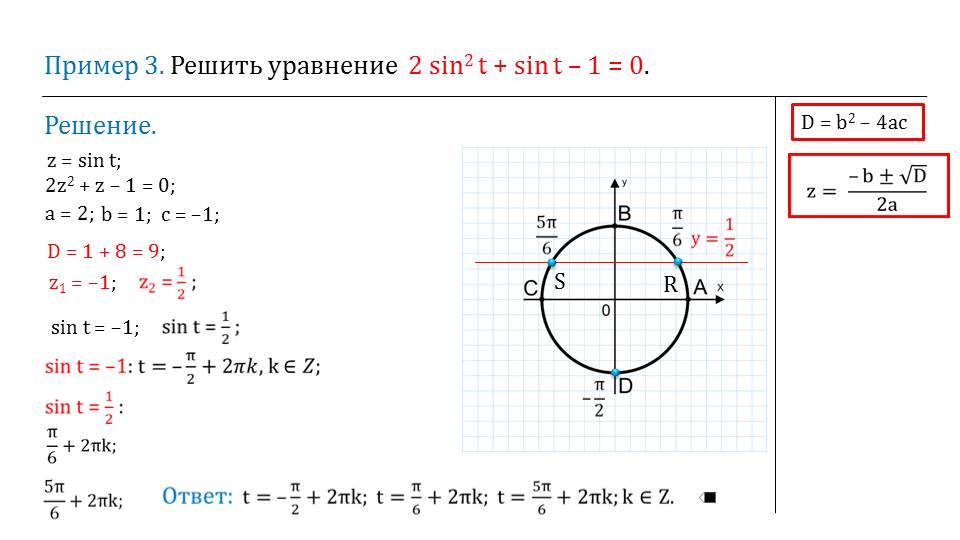
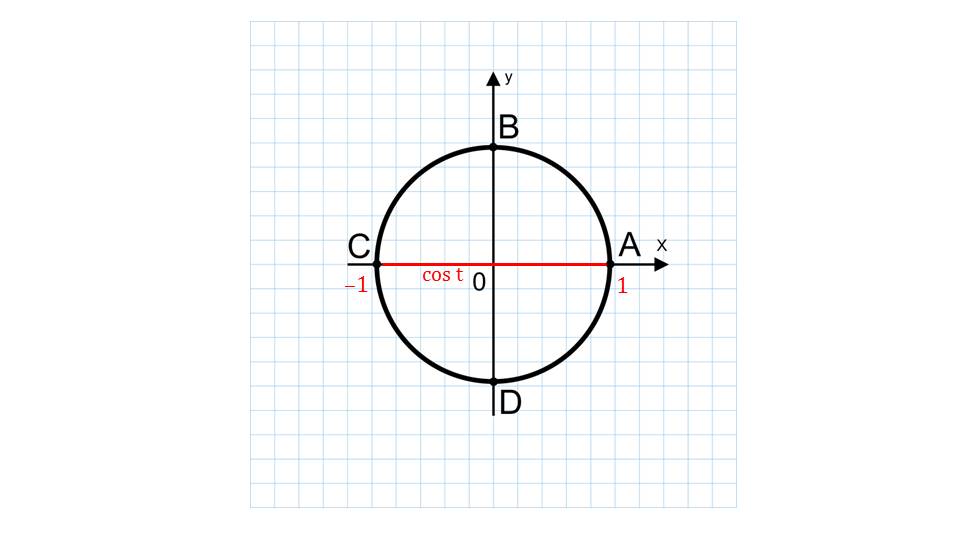
Чтобы показать геометрически область определения функции тангенса, на следующем слайде выводится иллюстрация. На ней изображены координатные прямые х и у, и область определения. Мы видим, что некоторые точки не включаются в график. Они обозначены красным пунктиром.

Второе свойство функции тангенс х это то, что она является периодической. А период равняется Пи. Ниже приводится формула, которая демонстрирует смысл периодичности. Далее выводятся некоторые основные тождества, которые справедливы для аргумента тангенса. Эти свойства касаются и котангенса.


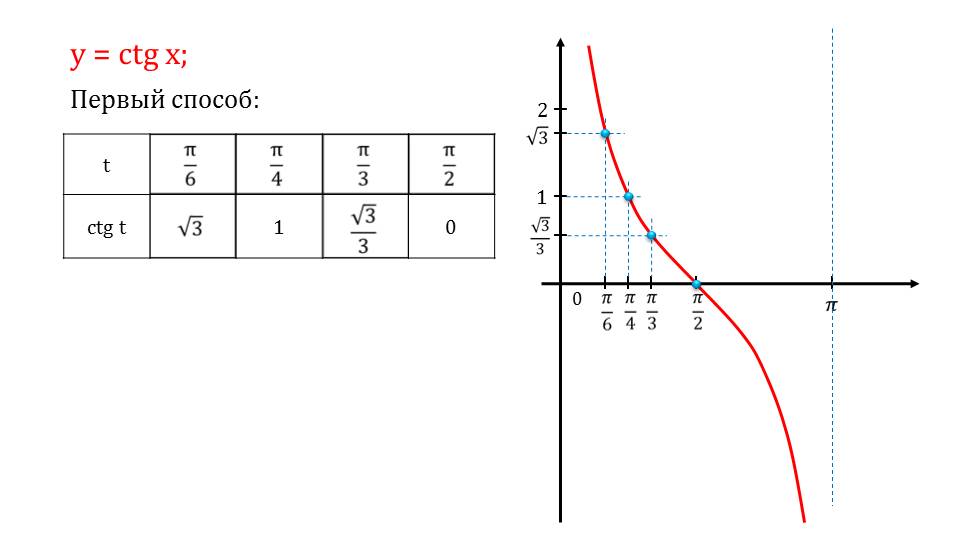
На следующем этапе начинается процесс построения графика тангенса. Проводится оно поточечно, методом подстановки, чтобы показать подробно. Можно увидеть, как посчитана каждая точка и отмечена на координатой плоскости. Так как функция является периодической, она будет растянута влево и вправо по оси ОХ. Однако можно заметить, что в некоторых точках функция не имеет значений.


Четвертое свойство гласит о том, что на определенном промежутке функция возрастает. Данный интервал выведен на слайде в формулировке свойства.
Также говорится о том, что функция не является ограниченной ни сверху, ни снизу. Это очевидно и наглядно продемонстрировано на графике. Так как функции тангенса и котангенса не являются ограниченными, они не имеют ни точку максимума, ни точку минимума. Запомнить это будет просто, если понять предыдущее свойства.

Что касается непрерывности, то функция не имеет точек разрыва и острых пиков. То есть функции тангенса и котангенса являются непрерывными.
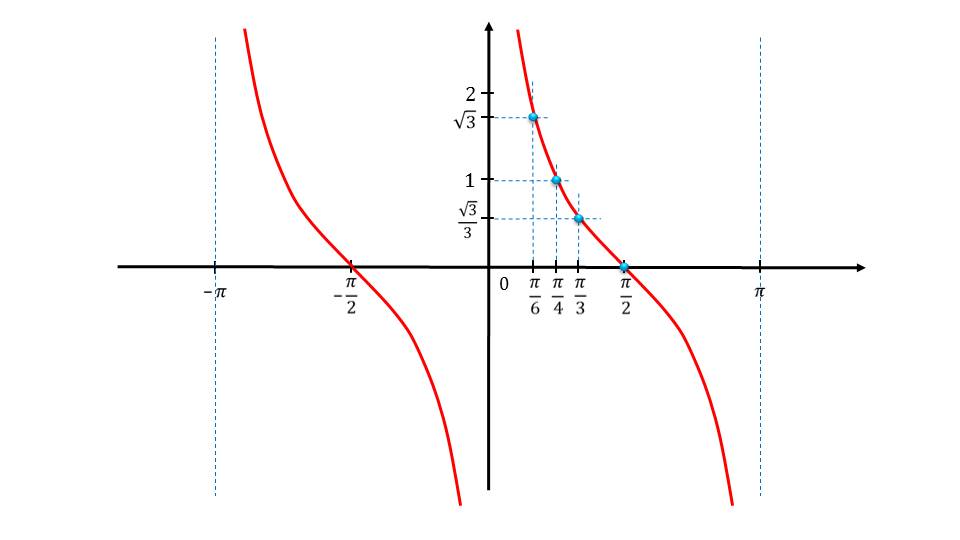
Что касается области значения функции, то она охватывает всю числовую ось. Это видно и на графике, можно доказать алгебраически также. Имеются асимптоты. Функции асимптоты выводятся на слайде.
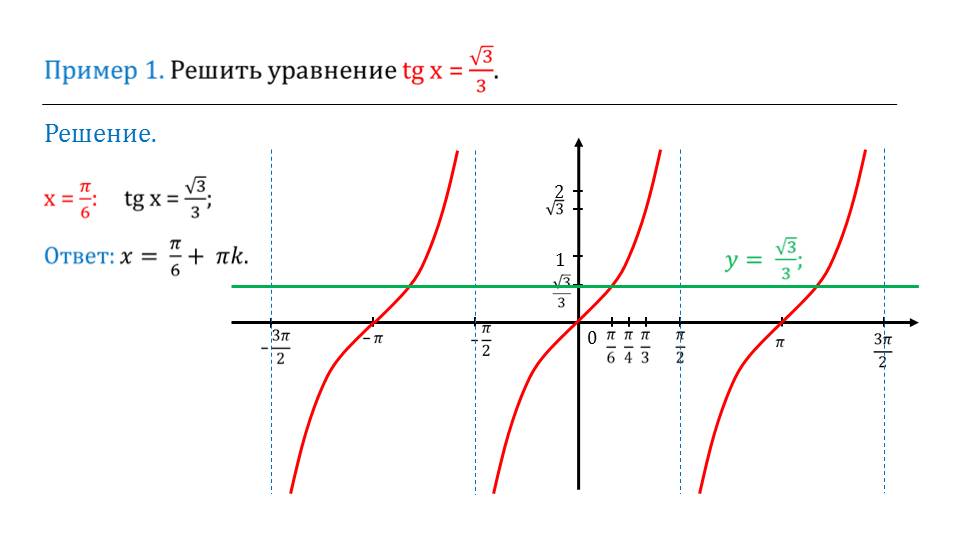
Ниже предлагается решить уравнение, которое содержит тангенс. Решить его можно очень просто геометрическим путем. Для этого необходимо построить график функции, которая представляет собой левую часть уравнения, и правую. В левой части мы видим тангенс, а в правой – функцию прямой. После построения этих графиков можно заметить, что они пересекаются. Множество точек пересечений и являются множеством решений данной функции. Учитель может объяснить данный пример на уроке и предоставить возможность школьникам решить аналогичные примеры самостоятельно. Благодаря этому, они смогут закрепить изученный материал.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 12397 |
| Номер материала | 804 |