
Презентация "Функция y=x^2. Степенная функция с четным показателем"

Краткое описание документа:
Начните урок с презентации темы. Дети должны знать, что данный урок посвящён степенной функции с чётным показателем, её свойствам и графику. Изначально тема может быть непонятна ученикам, поэтому важно сразу же ввести все необходимые определения и разъяснения.


слайды 1-2 (Тема презентации "Функция y=x^2. Степенная функция с четным показателем", пример)
Первое и самое важное определение – что такое степенная функция. Стоит написать несколько примеров степенных функций с различными переменными, чтобы показать, где расположена независимая переменная, а где показатель степени, который является натуральным числом. Первый пример учитель показывает, а далее просит учеников проанализировать уравнения. Убедитесь, что все ученики оперируют понятиями, поэтому не скупитесь на примеры при необходимости. Дети должны свободно владеть теоретическим материалом до того, как они приступят к практике.

слайды 3-4 (примеры)
Изучение степенной функции с чётным показателем необходимо начать с рассмотрения квадратичной функции. Уточните у учеников, какие цифры являют чётными и нечётными, попросите их привести примеры. Далее стоит более подробно остановиться на свойствах, которые характерны функции «у», равной «х» в квадрате.
Первое и наиболее простое свойство - равенство функции нулю, когда аргумент сам является нулем (Кто помнит, чему равен ноль в степени два, в степени семь и пятнадцать?), то есть абсолютно не важно, насколько высокий показатель степени функции, если аргумент равен нулю.
Для анализа следующего свойства желательно заранее задать вопрос, может ли число в квадрате получить отрицательное значение. Если ученики не поняли вопроса, то напишите на доске «а» во второй степени и спросите, может ли результат быть отрицательным. Приведите несколько примеров (например, четыре в квадрате, девять в квадрате). Таким образом, функция, где «х» в квадрате всегда будет принимать положительное значение.
Третье свойство говорит о том, что функция принимает как положительные, так и отрицательные значения аргумента. Данное утверждение говорит о том, что функция является чётной, а её график будет симметричен относительно оси «у».
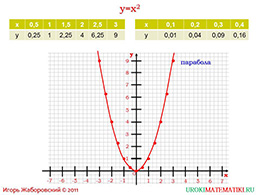
Для того чтобы подтвердить все предыдущие пункты, необходимо задать квадратичную функцию ученикам, предлагая им использовать значения аргумента от нуля до трёх в половинном промежутке. Более трёх не стоит брать значение аргумента, потому что придётся рисовать длинные оси координат (спросите у учеников почему). Когда все просчёты сделаны, то покажите, что фигура на доске – парабола, покажите её симметрию относительно оси «у». Спросите у учеников, что бы изменилось, если бы значения аргумента были те же самые, но отрицательные числа. Попросите одного из учеников изобразить новый график на доске в данных же координатах.
В обоих случая функция стремится, одна стоит сделать акцент на том, что при положительном значении аргумента парабола возрастает от нуля до плюс бесконечности, а при отрицательном значении аргумента график убывает от нуля до минус бесконечности. Поэтому важно не останавливать график на полученных точках, а довести его чуть дальше.
слайды 5 (пример)
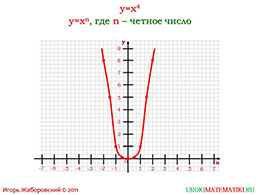
Далее представьте функцию, где показатель степени равен четырём. Изначально график нарисуйте примерно, на глаз. После этого попросите учеников просчитать точки для того, чтобы построить более точный график и нанести его на этих же осях координат. Какие видны изменения относительно симметрии графика? Изменилась ли ось, относительно которой симметрична парабола? Почему? Подытожьте урок перечислением того, что теперь известно определение степенной функции (какое оно), изучены все характерные свойства и известно, что график функции представлен симметричной фигурой – параболой.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5412 |
| Номер материала | 213 |