
Урок "Линейная функция и ее график"

Краткое описание документа:
Рассмотрим примеры функций, задаваемые формулой y=kx+b, где x– переменная, k иb– какие-то числа.
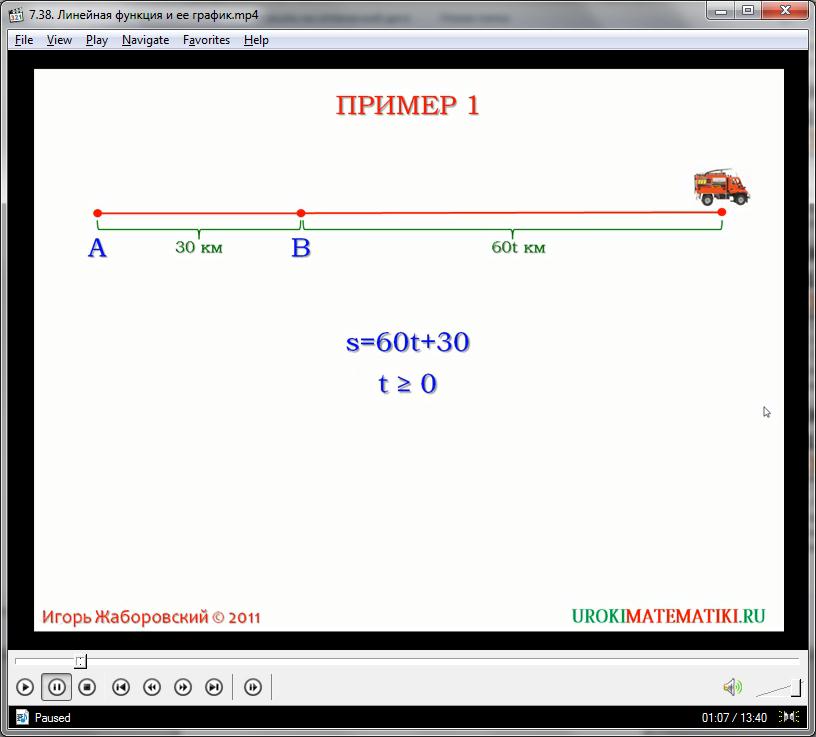
Пример 1. Автомобиль, который выехал из города A, в данный момент времени находится в поселке В, удаленном от А на 30 км. Двигаясь с постоянной скоростью 60 километров в час, за t часов преодолеет 60tкилометров и будетнаходиться от городаA на расстоянииравном (60t+30)км. Обозначимвыражение 60t+30 буквойs и получим формулу s=60t+30, где t – неотрицательное. Если необходимо найти расстояние, на котором находится автомобиль от города A через 5 часов, необходимо 60 умножить на 5 и прибавить 30.
Пример 2. Масса пустого бидона вместимостью 45 литров равна 5 кг, а масса оного литра жидкости – 0,9 кг. Тогда масса m (в килограммах) бидона, в котором содержится pлитровжидкости, равна (0,9p+5) кг. Формулой p=0,9p+5, где pнаходится в пределах от 0 до 45, задана функция.
В каждом из этих примеров мы имеем дело с функцией, которая задается формулой, в правой части которой многочлен первой степени с одной переменной. Когда (независимую) переменную обозначить буквой x, а зависимую – буквой y, то формула представима в виде y=kx+b, где k иb– любые числа.Эти функции линейные; функция называется линейной, если задается формулой вида y=kx+b, где x– переменная (независимая), k и b – произвольные числа.
Прямую пропорциональность можно рассматривать как один из частных случаев линейной функции. Ведь, при b=0 и k≠0 формула примет вид y=kx, а этой формулой задается прямая пропорциональность.
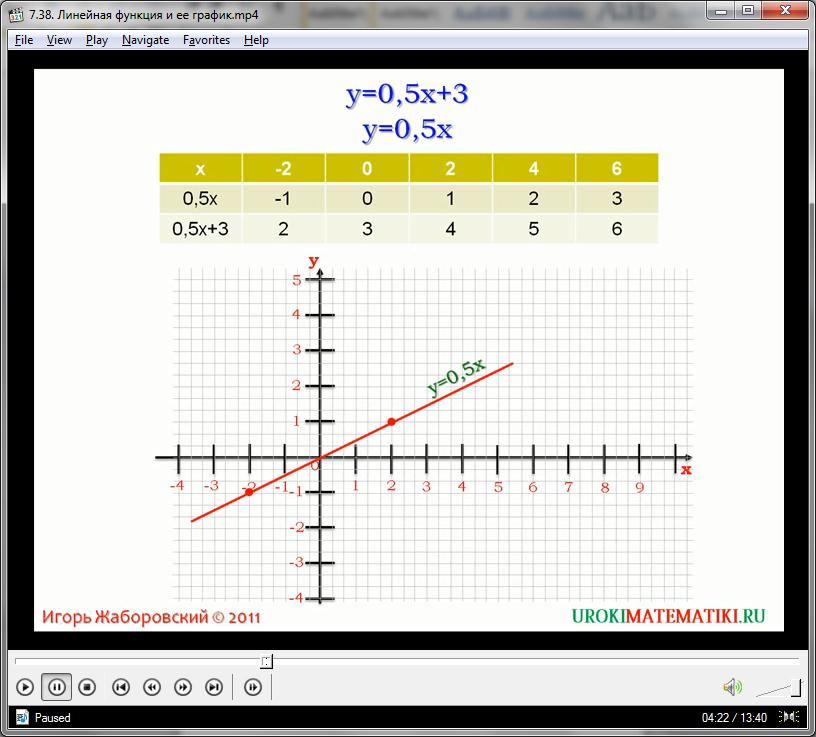
Интересно, какой вид имеет график линейной функции? Для выяснения исследуем линейную функцию y=0,5x+3. Для построения её графика используем график функции y=0,5x. Будем сравнивать соответствующие значения функций y=0,5x+3 и y=0,5x при одинаковых x. Из данной таблицы видно, что значения функции y=0,5x+3 при x больше на 3 значений функции y=0,5x при тех же значениях x. Каждой точке графика функции y=0,5x соответствует точка графика функции y=0,5x+3 с той же абсциссой и ординатой на 3 больше. Причем на графике функции y=0,5x+3 других, лишних точек нет.
График функции y=0,5x+3 получается из графика функции y=0,5x сдвигом каждой его точки на 3 значения вверх, то есть по направлению оси. Образно говоря, прямую y=0,5x переместим вверх на 3 единицы. Значит, графиком функции y=0,5x+3 является прямая параллельная прямой y=0,5x и проходящая через точку с координатами (0;3).
Аналогично доказывается, что график функции y=2x-1 – прямая, параллельная прямой y=2x и проходящая через точку (0;-1), то есть сдвинутая на 1 вниз, по направлению противоположному направлению оси Y.
Вообще график функции y=kx+b, где k≠0, есть прямая, которая параллельна прямой y=kx. Если же k=0, то формула принимает вид y=0x+b, то есть y=b. В этом случае функция при любом значении х принимает одно и то же значение. Для примера построим график функции y=-3. В результате получим прямую, параллельную оси ОХ, проходящую через точку (0; -3). В этом случае от x ничего не зависит: yвсегдапринимаетзначение -3.
Значит, графиклинейнойфункции – это прямая линия.
Заметим, что областью определения линейной функции y=kx+b, где k≠0, есть множество чисел, а областью значений тоже множество чисел или b, если k=0.
Для построения графика линейной функции достаточно найти две любые точки графика, отложить их на плоскости эти точки и использовать для построения прямой.
Пример 3. Построим график функции y=2x-3. Эта функция линейная и графиком будет прямая. Возьмём два произвольных значения аргумента x, например, x=0 и x=4 и вычислим соответствующие им значения функции. Если x=0,то y=2×0-3=-3 и при x=4, y=2×4-3=5. Отметим в координатной плоскости точки А(0;-3) и В(4;5) и проведем через них прямую АВ. Эта прямая и есть график функции y=2x-3.
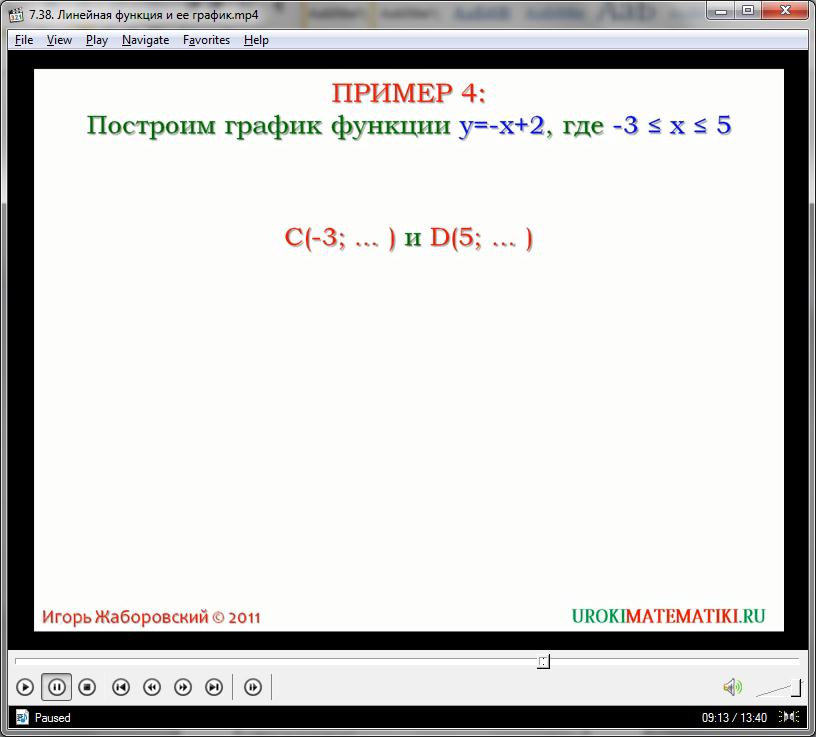
Пример 4. Построим график функции y=-x+2, при x в пределах от -3 до 5 включительно. График линейной функции y=-x+2 прямая, а график данной функции часть этой прямой, ограниченная точками с абсциссами -3 и 5, С(-3;…) и D(5;…). Мы не можем брать значения x меньше -3 и больше 5. Поэтому график функции это часть прямой. Вычислим ординаты точек С и D. Если x=-3, то y=-(-3)+2=5, а при x=5 y=-5+2=-3. Отметим в координатной плоскости точки C(-3;5) и D(5;-3) и соединим их отрезком прямой. Получим график функции y=-x+2, при x в пределах от -3 до 5 включительно. В отличие от предыдущего примера, график данной функции не прямая, а отрезок прямой. Поэтому область значений функции есть множество чисел от -3 до 5 включительно.
При построении графика функции важно знать, какова её область определения, а также координаты точек пересечения графика с осями координат.
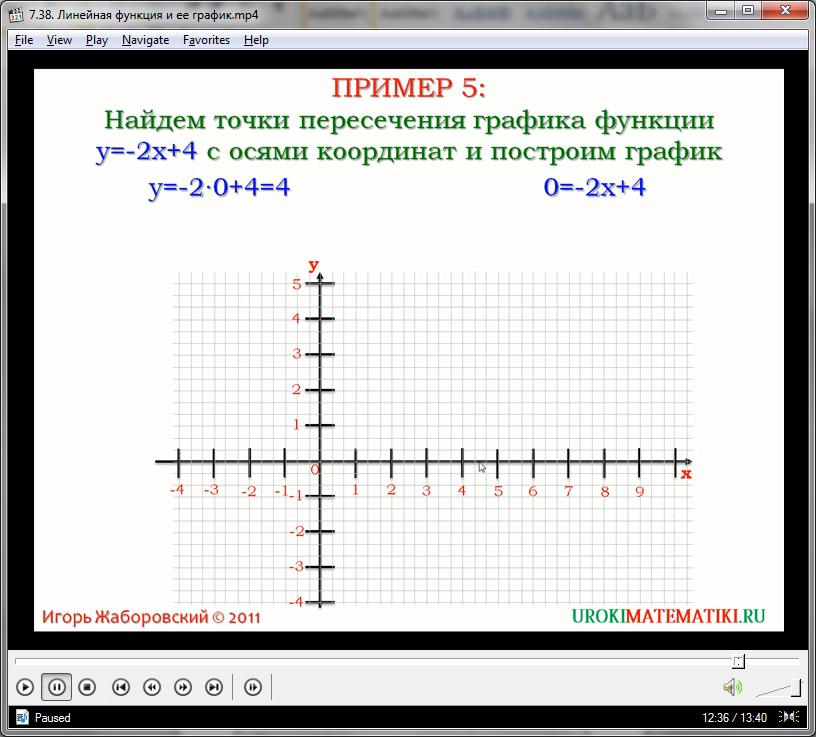
Пример 5. Найдем в каких точках пересекается график функции y=-2x+4 с осями Х и У, построим график. Для нахождения координаты у, пусть x=0. Найдем значение функции для этой точки y=-2×0+4=4. Получим точку M(0;4). Ордината любой точки, лежащей на оси абсцисс, равна 0. Поэтому чтобы найти координаты х, возьмём для y значение 0, а искомое значение найдём из уравнения функции. Получим уравнение 0=-2x+4. Решая его – 2x=4, x=2 – получаем точку N(2;0). Отметим полученные точки на координатной плоскости и построим прямую. MN и будет графиком функции y=-2x+4, а точки Mи N – точки графика функции на осях Х и У.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8076 |
| Номер материала | 470 |