
Урок "Прямая пропорциональность"

Краткое описание документа:
Мы уже ознакомились с базовым определением функции и с общими правилами графического отображения математических зависимостей. Общие правила позволяют понять сам смысл существования данных алгебраических объектов, а также упрощают работу с усложненными вариантами зависимостей.
Однако на практике часто пользуются набором стандартных функций, обладающих характерным графиком и определенными специфическими свойствами. В подавляющем большинстве математических задач используются именно этот комплекс зависимостей.
Наиболее простым видом функции является прямая пропорциональность. Предположим, у нас есть зависимость вида:
у = kх
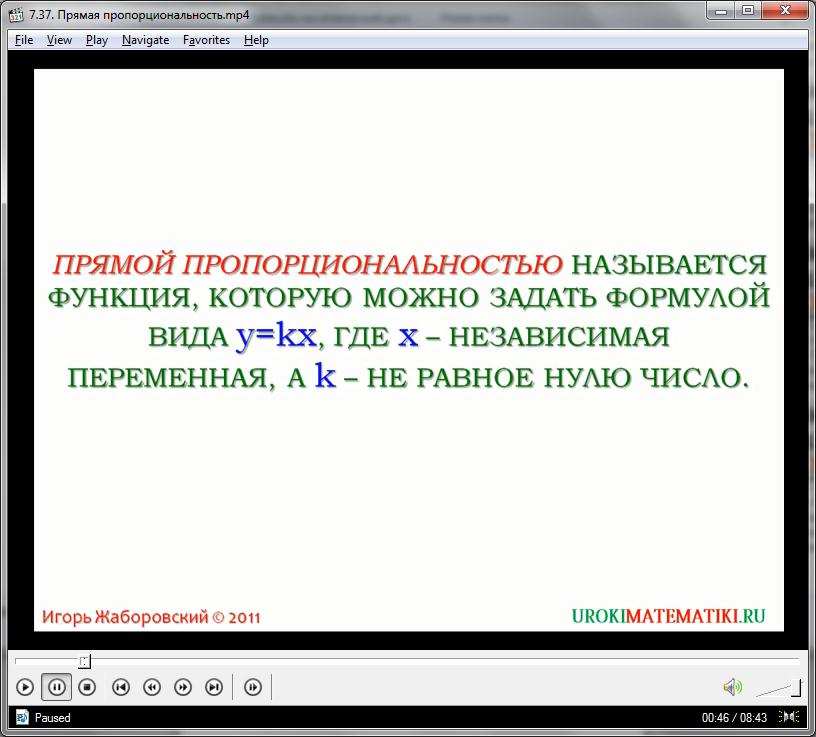
При этом k является неким одночленом, не равным нулю. Подобную функцию, которая выражает зависимость между у и произведением х на некое выражение, называют прямой пропорциональностью. Моном k, в данном случае, называется коэффициентом пропорциональности.
Рассмотрим формулу нахождения периметра квадрата по заданной стороне. Как известно, периметр данной фигуры равен учетверенному значению любой из сторон:
Р = 4а
Данную формулу легко можно преобразовать в функцию вида:
у = 4х
Функция выражает зависимость между периметром и стороной квадрата. Как можно понять из видео, эта зависимость является формулой прямой пропорциональности с коэффициентом k = 4. Иначе говорят «периметр квадрата прямо пропорционален его стороне».
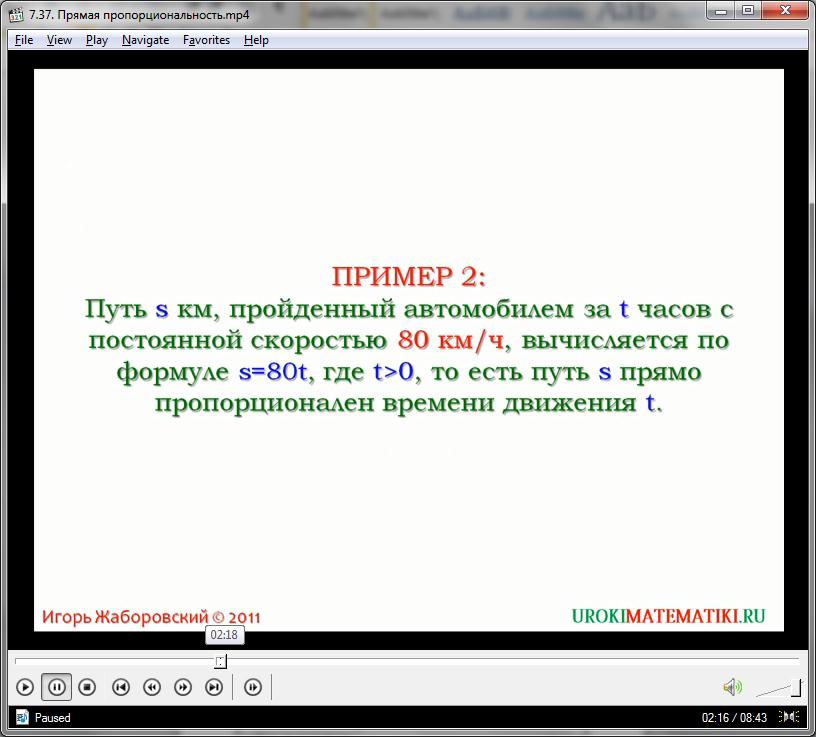
В жизни встречается довольно много зависимостей, имеющих прямо пропорциональный характер. Например, даже руководствуясь исключительно логикой, можно сделать вывод, что цена на любой товар прямо пропорциональна либо его весу, либо количеству единиц товара. Если что-либо продается по цене 10 р за килограмм, то общая стоимость такого товара прямо пропорциональна его массе и составляет:
с = 10а,
где с – стоимость, а – масса товара в килограммах. Преобразуем формулу в функцию:
у = 10х,
где 10 – это коэффициент, задаваемый переменной характеристикой – ценой.
Изучим график функции прямой пропорциональности. Предположим, дана функция вида:
у = 2х
Рассчитываем координатную сетку на промежутке х (-3, у) (3, у):
х = -3 у = 2(-3) = -6
х = -2 у = 2(-2) = -4
х = -1 у = 2(-1) = -2
х = 0 у = 2(0) = 0
х = 1 у = 2(1) = 2
х = 2 у = 2(2) = 4
х = 3 у = 2(3) = 6
Отмечаем все точки на декартовой системе координат, соединяем их в одну общую линию. На видео представлен график прямой пропорциональности. Это прямая линия, проходящая через центр координат (в точке 0, 0). Стоит отметить, что в пределах одного типа графики функций весьма похожи, а наличествующие различия легко объясняются нюансами формулы. Например, для всех функций вида:
у = kх
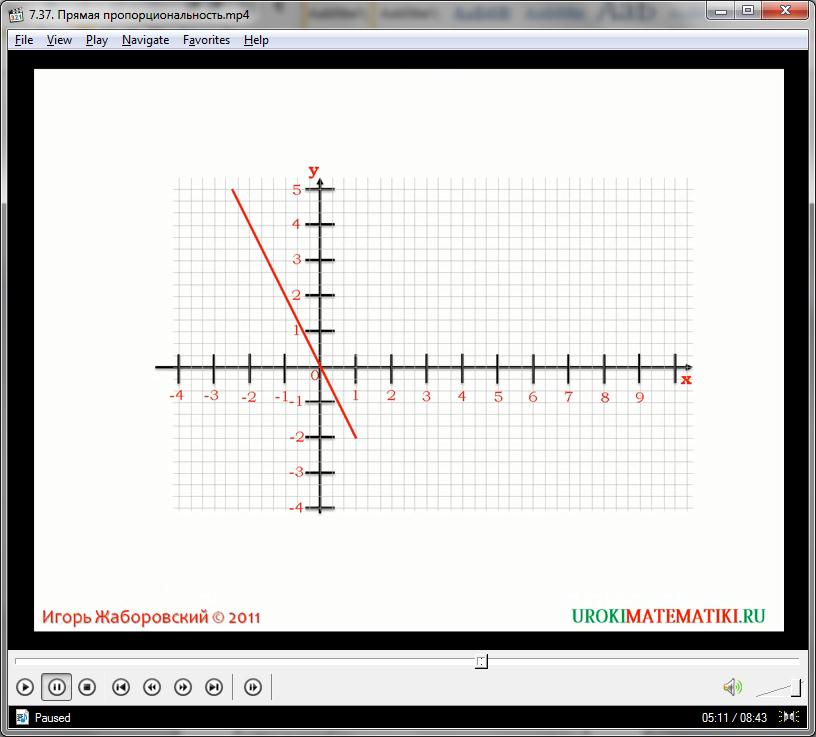
Если k положительна – то прямая линия идет с третьей четверти (-х, -у) в первую (х, у). Если же k меньше нуля, то прямая графика идет со второй четверти (-х, у) в четвертую (-х, -у). Но, в любом случае, график прямой пропорциональности представлен прямой бесконечной линией, как правило, существующей беспрерывно, на всех промежутках обеих множеств.
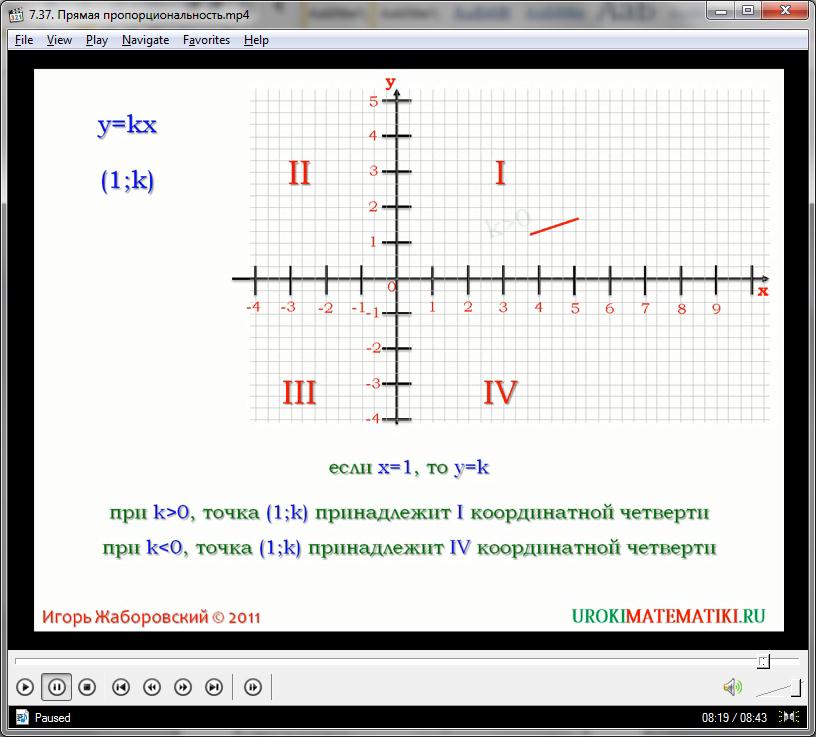
Форма графика вида у = kх может характеризоваться только одним показателем – коэффициентом, который графически обуславливает угол между прямой и осью абсцисс. Чем больше значение k, тем больше данный угол и наоборот.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4871 |
| Номер материала | 464 |