
Презентация "Прямая пропорциональность"

Краткое описание документа:
Начните урок с вопроса о том, что такое пропорциональность? В итоге скажите, что это взаимная зависимость величин, когда значение одной равно значению другой.


слайды 1-2 (Тема презентации "Прямая пропорциональность", определение прямой пропорциональности)
Если мы говорим о прямой пропорциональности, то здесь уже касаемся функциональной зависимости, то есть одна часть зависит от другой, когда их отношение постоянно. Получаем, что данные изменяют пропорционально.
Далее стоит более подробно остановиться на определении прямой пропорциональности и показать, какой формулой она задаётся, где независимая переменная расположена, а где коэффициент, который не равен нулю. Сразу стоит ответить на вопросы: почему переменная независима и почему коэффициент k не может быть равен нулю. Стоит отметить, что второе название коэффициента k – коэффициент прямой пропорциональности.


слайды 3-4 (примеры)
Рассмотрите с учащимися следующую задачу: периметр квадрата выступает функцией длины его стороны, данная функция имеет определённую формулу, а её переменные выбираются в идентичных линейных единицах. Это пример прямой пропорциональности! Напишите на доске формулу и введите конкретные данные (например, пять и восемь для переменной «а»). Далее отношение переменных постройте в пропорцию, чтобы учащиеся видели, что функция просто изменилась в какое-то количество раз.
Когда решение одного примера учитель разобрал вместе с классом, стоит перейти ко второму самостоятельному примеру: задача, где вводятся переменные расстояния и времени. Мы знаем, с какой скоростью шёл автомобиль, и понимаем, по какой формуле высчитывается расстояние. Следовательно, видим, что путь прямо пропорционален времени движения автомобиля. В идеале – услышать этот ответ от одного из учеников, в ином случае – вновь поэтапно объясните пример.

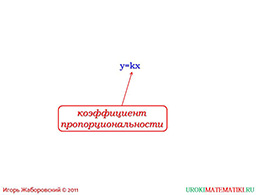
слайды 5-6 (пример, коэффициент пропорциональности)
Третий пример или закрепляющий: где речь идёт о товаре по определённой цене. Введены переменные товару и его массе в килограммах. Какая зависимость у данных переменных?
Вернитесь к обсуждению коэффициента пропорциональности. Кто запомнил, почему он не может равняться нулю? Какое второе его название? Данный слайд наглядно показывает расположение коэффициента перед независимой переменной.
слайды 7-8 (примеры)
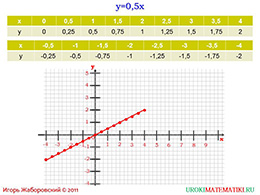
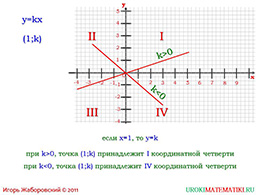
Теперь необходимо вовлечь учеников следующей функцией, где зависимость «у» от «х» является прямой пропорциональностью. Можно взять небольшие значения для «х» (например, от минус четырёх до четырёх) и просчитать значения «у» в данном случае. Спросить, у кого функция восходит, а у кого нисходит. Если найдены ошибки, то исправить их, показывая правильный вариант.
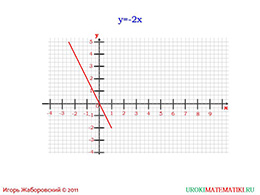
Для того чтобы получить отличающийся график, возьмите функцию с отрицательным коэффициентом. Вновь попросите учеников подобрать небольшие значение для «х» и рассчитать показания «у». После сбора данных, ученикам стоит изобразить график в тетради и подумать, почему теперь график стал нисходящим. Какие ещё характерные особенности для обоих графиков они видят?

слайды 9-10 (примеры)
Сделать вывод по этим примерам, что график прямой пропорциональности выглядит в виде прямой, которая проходит через начало координат.
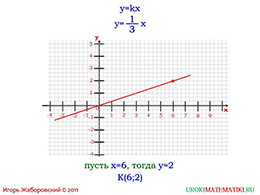
Теперь приведите пример графика, когда коэффициент является дробным числом. Попросите одного из учеников изобразить график на доске и проанализировать, что изменилось.
слайды 11-12 (примеры)
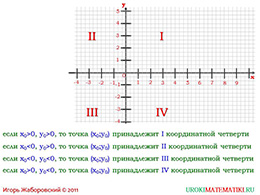
Теперь стоит свести вместе всю теорию и обратить внимание учеников на том, что именно от того, какие значения у переменных, будет зависеть, где расположены точки прямой. А то, каким числом является коэффициент прямой пропорциональности, влияет на расположение сторон функции. Обязательно покажите, как нумеруется каждая из четвертей и, рассматривая варианты, вспомните примеры, которые использовались на уроке.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6034 |
| Номер материала | 205 |