
Урок "Взаимное расположение графиков линейных функций"

Краткое описание документа:
Расположение графика функции У равно КХ плюс В на координатной плоскости напрямую зависит от значения коэффициентов К и В. Спросим: как зависит расположение графика от коэффициента В. Если Х=0, то У=В. Значит график линейной функции У равно КХ плюс В при любых значениях К и В обязательно проходит через точку с координатами (0; В). От К зависит угол, который образует прямая У равно КХ плюс В с осью Х.
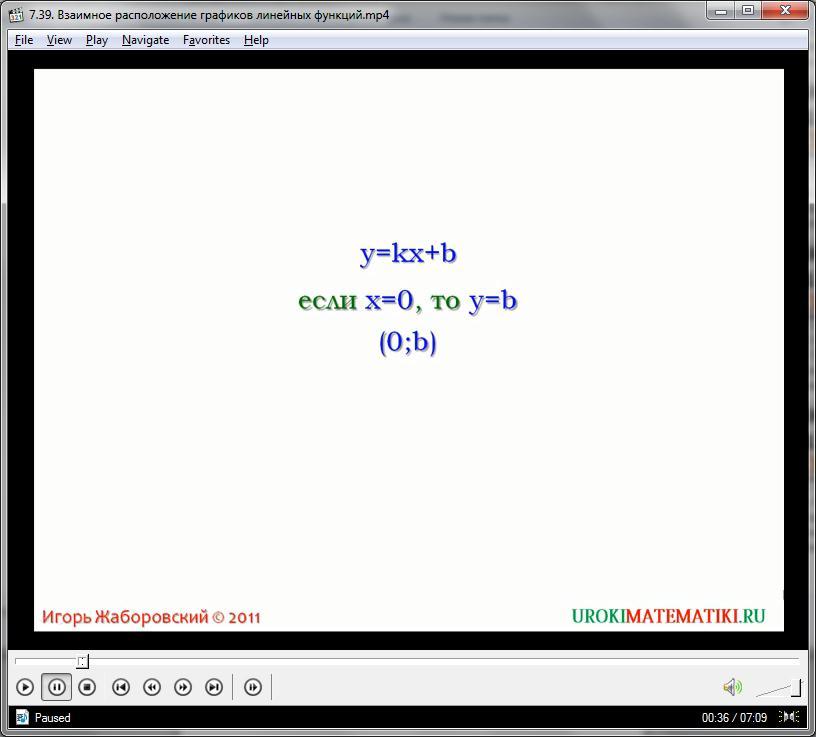
Например, прямая У равно КХ плюс В при К=1 и наклонена к оси Х под углом сорок пять градусов. Это следует из того, что прямая У=Х совпадает с биссектрисами первого и третьего координатных углов. Если К больше нуля, то угол наклона прямой У равно КХ плюс В к оси Х острый. Если же К меньше нуля, то этот угол тупой. Поэтому коэффициент К называют угловым коэффициентом прямой графика функции У равно КХ плюс В.
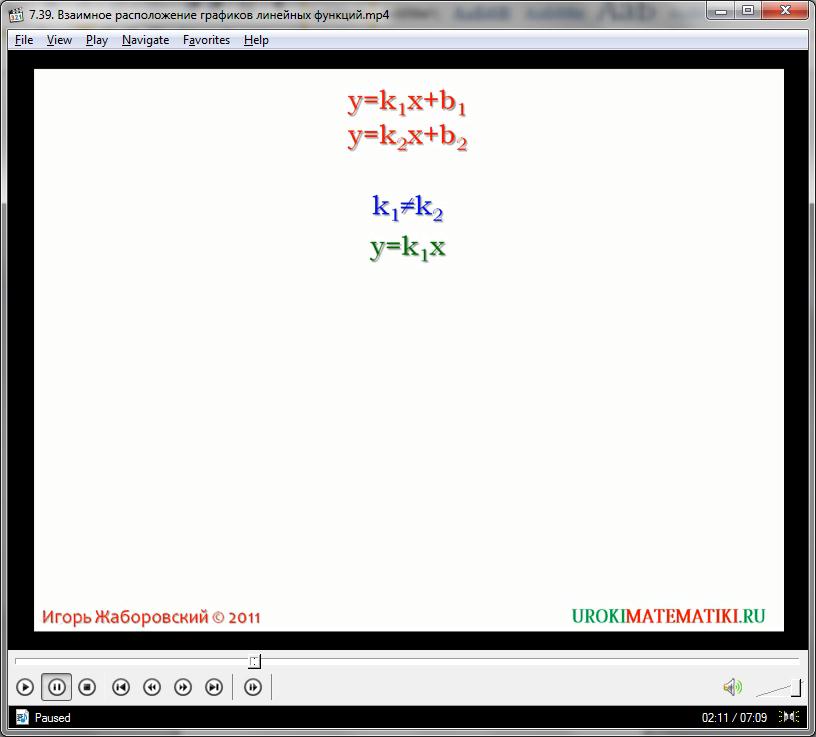
Выясним, каково взаимное расположение графиков функций двух линейных функций: У равно К1Х плюс В1 и У равно К2Х плюс В2 на координатной плоскости. Графики этих функций прямые. Они могут пересекаться, то есть –иметь только одну общую точку, или быть параллельными, то есть – не иметь общих точек. Если К1 не равно К2, то прямые пересекаются, так как первая из них параллельна графику прямой пропорциональности У равняется К1Х, а вторая графику прямой пропорциональности У равно К2Х. А этими графиками являются две пересекающиеся прямые. Если К1 равно К2, то прямые параллельные, так как каждая из них параллельная графику прямой пропорциональности У равно КХ, где К равно К1и равно К2.
Заметим, что случаи, когда К1 равно К2 и В1 равно В2 мы не рассматриваем, так как речь идет о графиках двух различных функций. А при этом условии прямые У равно К1Х плюс В1 и У равно К2Х плюс В2 совпадают.
Итак, для любых двух линейных функций справедливо утверждение «Если угловые коэффициенты прямых, являющихся графиками линейных функций, различны, то прямые пересекаются, если же угловые коэффициенты прямых одинаковы, то прямые параллельны.» На рисунку мы видим графики различных линейных функций с угловыми коэффициентами и одинаковым значением В, равным двум. Эти графики пересекаются в точке с координатами ноль и два. На следующем рисунке изображены графики линейных функций с одинаковыми угловыми коэффициентами и различными значениями В. Эти прямые параллельны друг другу.
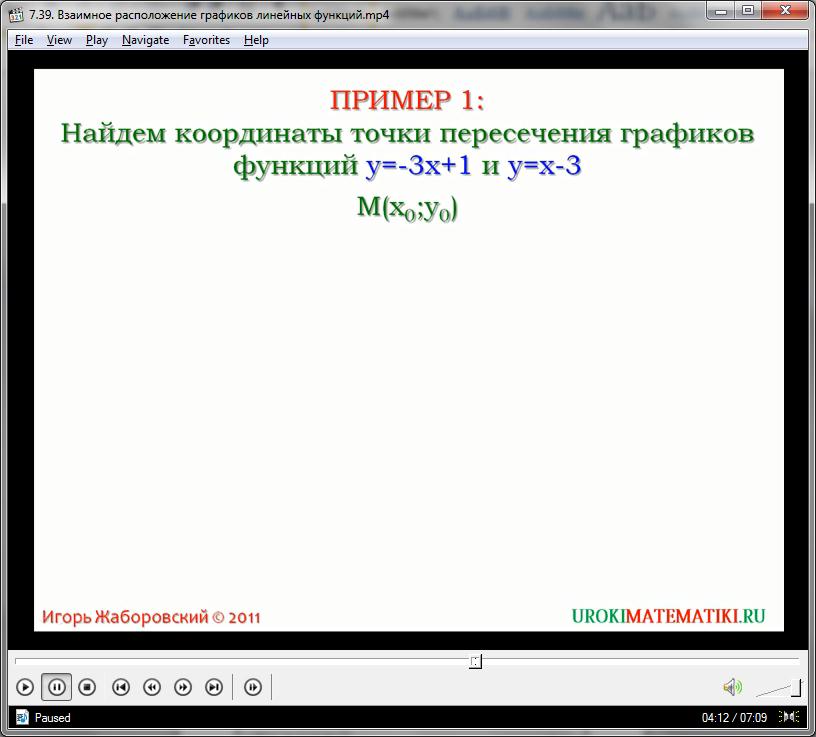
Пример один. Найдем координаты точек пересечения графиков функций: У равно минус 3Х плюс 1 и У равно Х минус 3. Будем рассуждать так: пусть точка М с координатами Х нулевое У нулевое – искомая точка пересечения графиков данных функций. Тогда ее координаты удовлетворяют как первое, так и второе уравнению. Значит, У нулевое равное минус 3Х нулевое плюс 1 и У нулевое равное Х нулевое минус 3 – это верные числовые равенства.
Отсюда получаем, что минус 3Х нулевое плюс 1 равно Х нулевое минус 3. Тогда минус 4Х нулевое равно минус 4, и Х нулевое тогда равно 1.
Подставим значение Х нулевое равно 1 в равенство У нулевое равно минус 3Х нулевое плюс 1 или в равенство У нулевое равно Х нулевое минус 3, получим У нулевое равно минус 2. Таким образом, точка пересечения графиков функций имеет такие координаты: Х нулевое равно 1, а У нулевое равно минус 2. Заметим, что часто неизвестные координаты не обозначают другими символами. В этом случае решение выглядит так: минус 3Х плюс 1 равно Х минус 3; минус 4Х равно минус 4, а Х равно 1. У равно 1 минус 3 и равно минус 2. (Или У равно минус 3 умножить на 1 плюс 1 равно минус 2.) Ответ: точка с координатами 1 и минус 2.
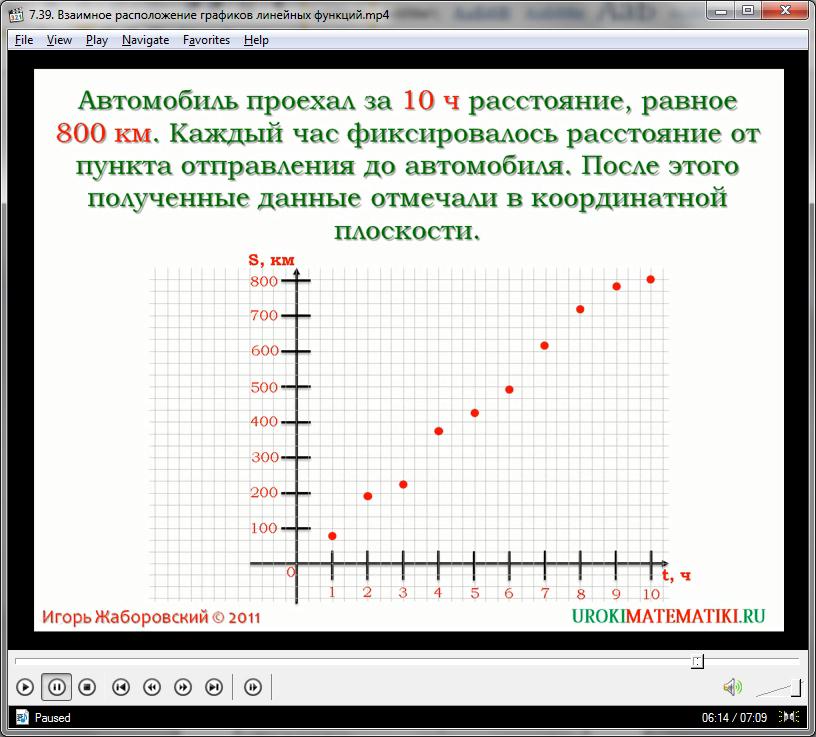
Линейная функция часто используется в статистике. Рассмотрим пример. Автомобиль проехал за 10 часов расстояние, равное 800 километров. Каждый час фиксировалось расстояние от пункта отправления до автомобиля. После этого полученные достаточно разбросанные данные отмечали в координатной плоскости. Отмеченные точки не лежат на одной прямой, поскольку на разных участках дороги автомобиль ехал с разной скоростью.
Однако все полученные точки группируются около так называемой аппроксимирующей прямой. Чтобы ее построить, нужно приложить к чертежу линейку и провести наиболее подходящую прямую, содержащую вблизи себя все отмеченные точки. Проведенная прямая позволяет прогнозировать, где может оказаться автомобиль через 11, 12 и так далее часов после начала своего движения. Заметим, что в статистике существуют специальные методы расчетов аппроксимирующих прямых, но и рассмотренный метод дает вполне разумное приближение.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5199 |
| Номер материала | 471 |