
Презентация "Линейная функция и ее график"

Краткое описание документа:
В презентации для 7-го класса на тему «Линейная функция и ее график» говорится о таком понятии как «линейная функция». В процессе работы до учащихся нужно будет донести главную мысль о том, что линейная функция должна содержать в себе необходимые условия при построении ее графика.


слайды 1-2 (Тема презентации " Линейная функция и ее график ", пример)
На первом слайде показана формула, по которой строиться каждая линейная формула. Соответственно, любая функция, которая принимает вид данной формулы, будет являться линейной. Эта формулу учащимися стоит выучить, чтобы в дальнейшем они могли построить по ней график линейной функции.

слайды 3-4 (примеры)
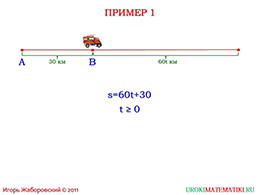
Чтобы школьникам стало более-менее понятно, как использовать данную формулу, необходимо разобрать несколько примеров, наглядно показывающих, каким именно образом нужно получать данные из конкретной задачи, чтобы потом их подставить вместо переменных этой формулы. Для этого и приводится первый пример.
Во втором примеры дана другая задача и с другими значениями для того, чтобы учащиеся имели возможность закрепить только что полученные знания по данной теме.


слайды 5-6 (пример, определение линейной функции)
На следующем слайде показаны результаты двух примеров, а именно два уравнения линейной функции, составленные по соответствующей формуле. Ниже она разобрана на отдельные составляющие. То есть тут до школьников важно донести, что линейная функция состоит из двух важных элементов, а точнее коэффициентов двучлена. Если ориентироваться по формуле, то ими являются переменные k и b.
Дальше учащимися должно быть тщательно разобрано определение самой линейной функции. В его формуле x является независимой переменной, в то время как k и b могут быть любыми числами. Для того чтобы сама линейная функция существовала, необходимо соблюдать некоторое условие. Оно гласит, что число b должно равняться при условии, что число k наоборот не должно равняться нулю.
слайды 7-8 (примеры)
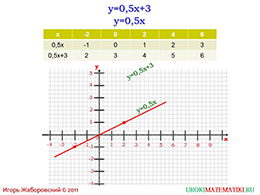
Для большей наглядности на следующем слайде приведен пример построения графика, составленный по формуле двумя способами. То есть при построении были учтены два условия: первое – коэффициент b равняется числу 3, второе – коэффициент b равняется нулю. С помощью презентации видно, что эти графики отличаются лишь расположением прямой по оси Y.
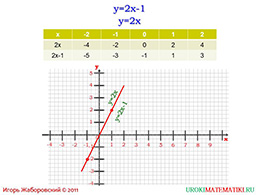
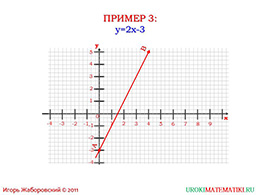
Во втором примере построения графика линейной функции учащиеся должны понять следующее: во-первых, график при коэффициенте k, равному нулю проходит через начало координат, а во-вторых, коэффициент k отвечает в зависимости от своего значения за степень наклона полученного графика по оси Y.

слайды 9-10 (пример, график линейной функции)
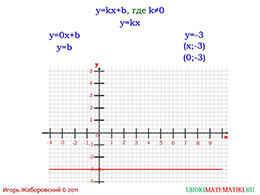
На следующем слайде разбирается пример особого графика, где коэффициент k равен нулю, а сама функция равна значению коэффициента b.
Итак, донеся до школьников вышеперечисленный материал, учитель теперь должен пояснить, что график, построенный с помощью линейной функции, всегда является линия, то есть прямая.


слайды 11-12 (примеры)
Далее необходимо объяснить учащимся, что в зависимости от условий значения коэффициентов k и b будет зависеть область определения, а также область значений самой линейной функции.
Теперь следует разобрать несколько примеров построения графиков для того, чтобы понять зависимость условий значения коэффициентов, а также научиться определять координаты точек на графике.
слайды 13-14 (примеры)
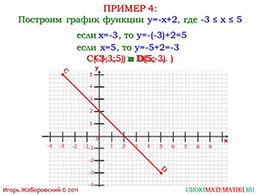
В примере под номером 4 ученики 7-го класса уже самостоятельно должны определить координаты графика в соответствии с условием.
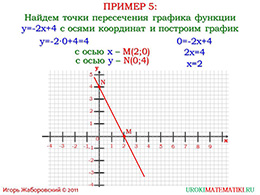
Следующий пример создан для того, чтобы школьникам стало максимально понятно каким образом строиться график линейной функции с положительным коэффициентом x, от которого напрямую зависит расположение прямой на оси X.
слайды 15-16 (примеры)
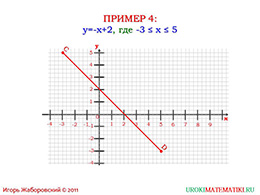
По этой же причине в презентации приведен пример построения графика при отрицательном значении коэффициента x.
В качестве последнего примера выступает график с отрицательным коэффициентом x. Чтобы его выполнить учащиеся должны определить координаты указанного графика и построить график, исходя из этих координат. На этом слайде презентация заканчивается.
Этот материал можно использовать как учителями при проведении уроков по учебной программе, так и школьниками при самостоятельном изучении материала. Наглядность данной презентации позволяет без особого труда понять учебный материал по данной тематике.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8144 |
| Номер материала | 211 |