
Презентация «Функция y=x^n»

Краткое описание документа:
Презентация «Функция » содержит наглядную информацию для объяснения учителя при изучении данной темы. В составе презентации представлено определение степенной функции, виды ее графиков, описание свойств. Задач данной презентации – улучшить качество обучения, улучшая наглядность и понятность учебного материала, способствовать быстрому его запоминанию и лучшему пониманию.
Использование презентации дает возможность улучшить качество преподавания. При помощи последовательного показа слайдов, материал структурирован и не требует доработки в процессе объяснения учителем. Применение анимационных эффектов улучшает наглядность информации, способствует концентрации внимания учеников на изучаемом предмете. Выделение цветом важных деталей и понятий способствует быстрому запоминанию материала, лучшему его усвоению.


В начале презентации представляется ее тема и дается определение. Для запоминания выделено название «степенная функция с натуральным показателем» и представлена данная зависимость y=xn, в которой x – независимая переменная, а n – натуральное число. На слайде представлены графики простейших степенных функций y=x,y=x2, y=x3. В первом случае это прямая, проходящая через начало координат и симметричная относительно начала координат. Во втором случае это парабола, в третьем случае – кубическая парабола.
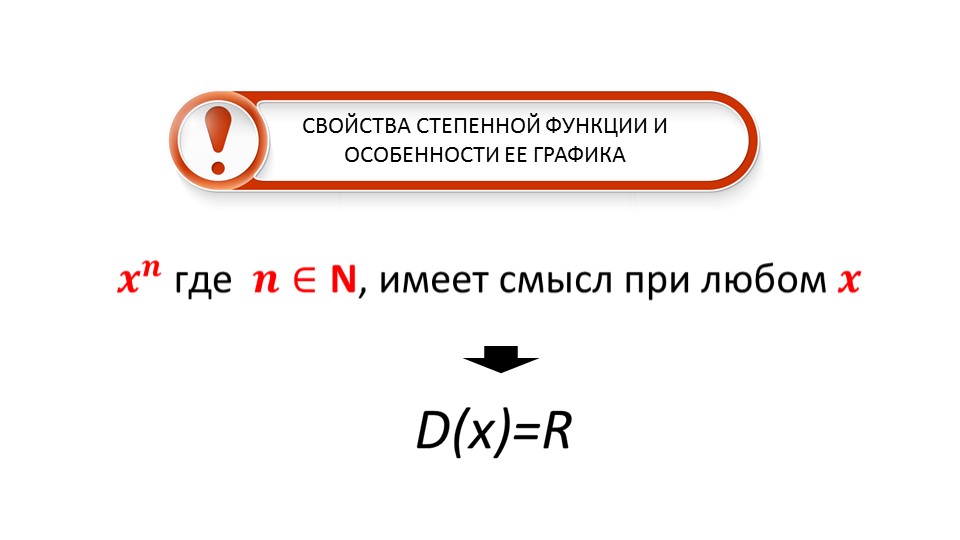
Свойства степенной функции рассматриваться, начиная с области ее определения. На слайде 4 замечено, что степенная функция с любым натуральным n будет иметь смысл во всем множестве действительных чисел. Область определения обозначена как D(x)=R.
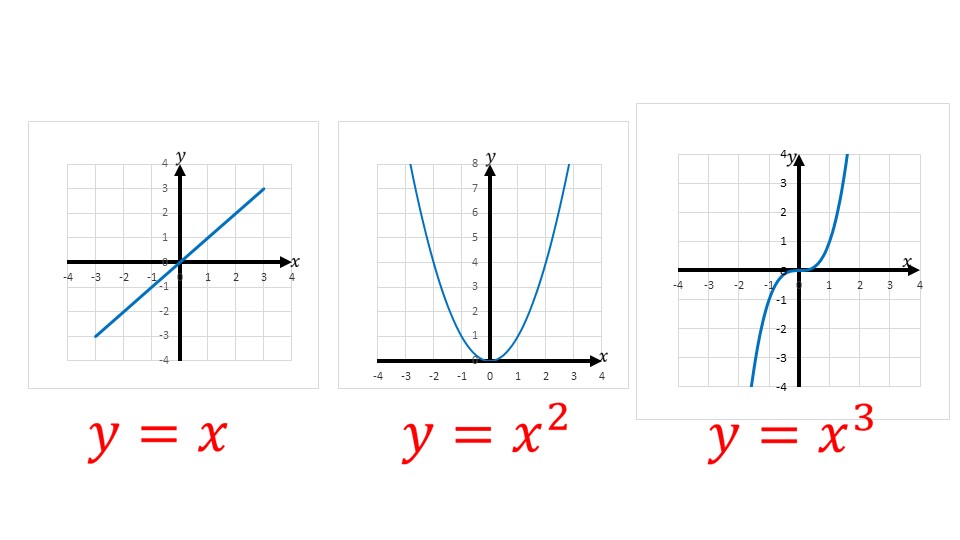
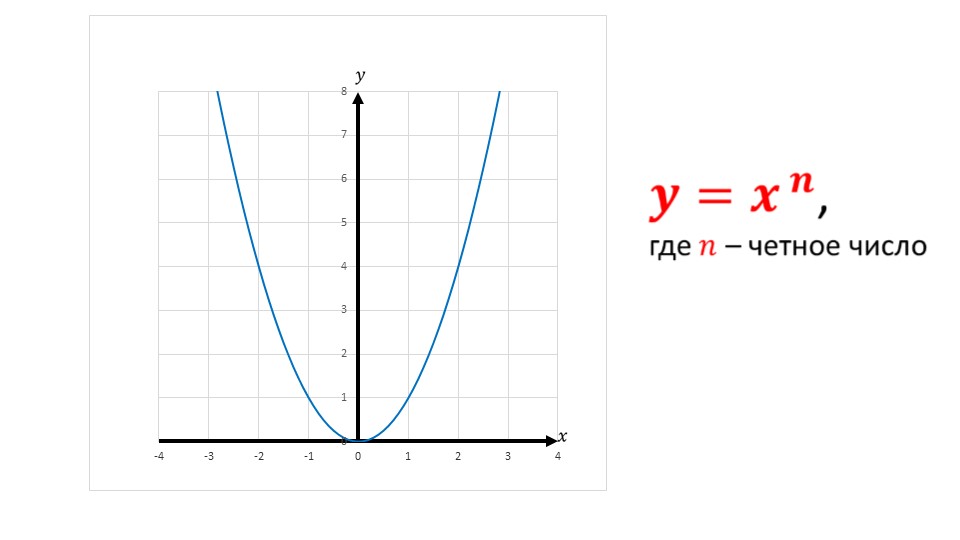
Далее описываются свойства функции y=xn, в которой n - четное число. Отмечается, что в этом случае свойства функции аналогичны свойствам квадратичной функции вида y=x2. График такой функции проходит через точку начала координат (0;0). При любых x значения функции всегда будут положительны, так как четная степень всегда приумножении дает знак плюс. Также противоположным значениям аргумента x соответствуют одинаковые значения данной функции, то есть верно равенство (-x)n=xn. Возрастание функции наблюдается на промежутке [0;+∞), а убывание функции наблюдается на промежутке (-∞;0]. Область значений функции охватывает все положительные значения действительной оси.


На слайде 6 особое внимание уделяется свойству 4, которое определяет промежутки возрастания функции, так как оно специфично для четного n. Отмечается, что возрастание функции означает, что при возрастании аргумента 0≤x1<x2 значения функции также растут x2n>x1n. Убывание функции на промежутке (-∞;0] сводится к следующему. При возрастании аргумента функции 0≥x2>x1, что означает 0≤-x2<x1. При подстановке данных аргументов в выражение функции получаем x2n<x1n.

На слайде 7 представлен график функции y=xn с четной степенью n. Далее отдельно рассматривается 5 свойство для степенной функции с четной степенью. Так как значения степенной функции с четной степенью всегда положительны или равны нулю, то любое y>0 является значением некоторой функции y=xn, где x – положительное число, а n – натуральное число.
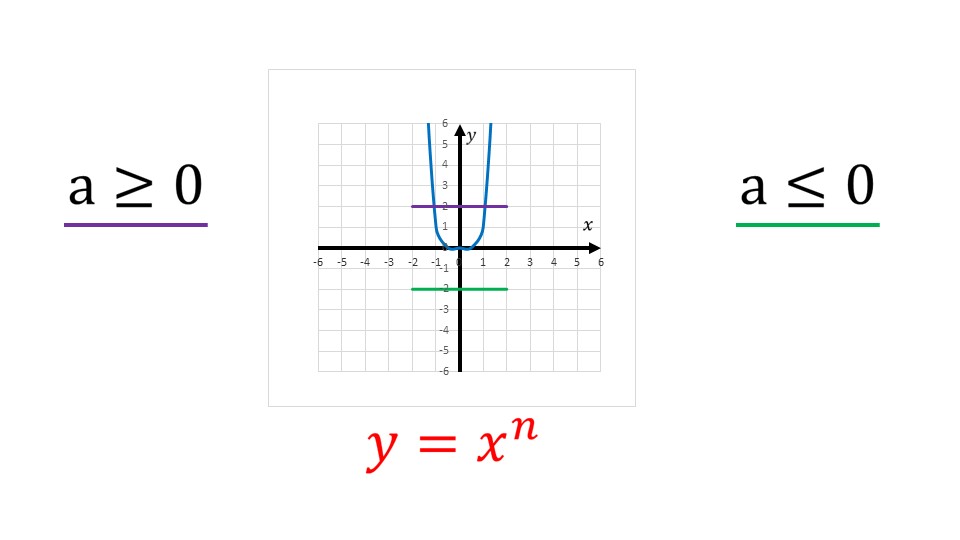
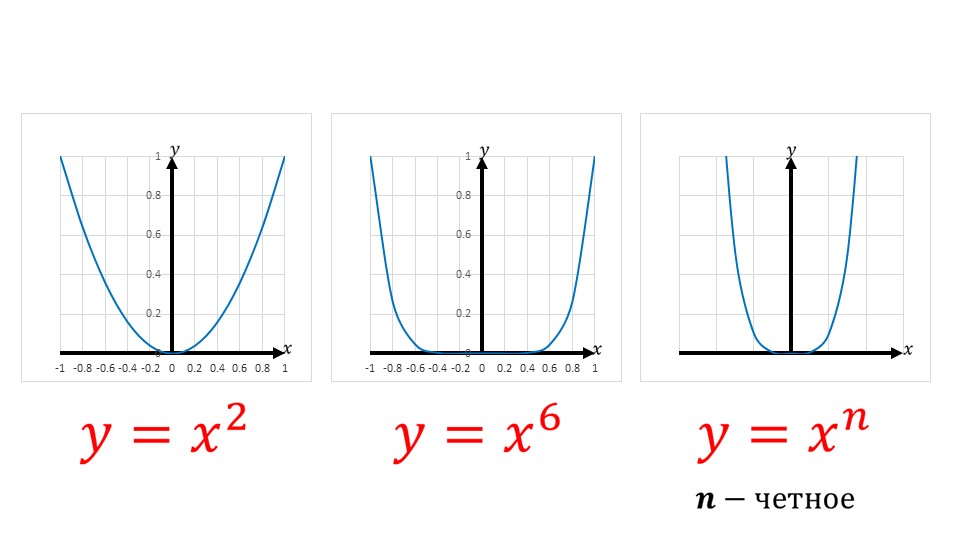
Следующие слайды демонстрируют варианты параболы для различных степенных функций с четным показателем степени.
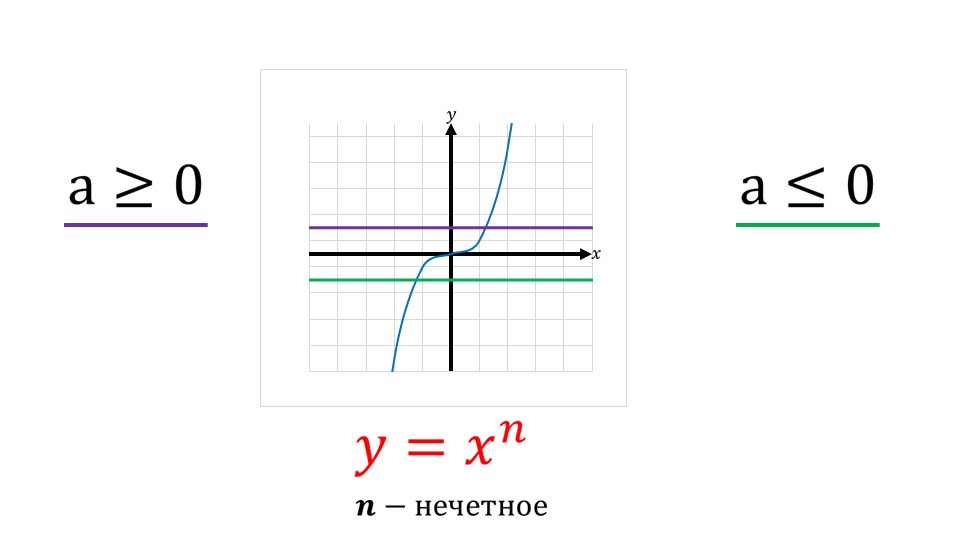
На слайде 11 рассматриваются свойства степенной функции y=xn с нечетным показателем степени. На слайде отмечается, что эти свойства аналогичны свойствам y=x3. График данной функции проходит через начало координат (0;0). При положительном значении аргумента значение функции также положительно, а при отрицательном значении аргумента – значение функции отрицательно. Таким образом, график располагается в первой и третьей четвертях системы координат. Противоположному значению аргумента соответствует противоположное значение функции, что следует из (-x)n=-xn. По всей области определения функции она возрастает. Также указана область значений функции, которая представлена всем множеством действительных чисел.


Свойство функции, характеризующее ее возрастание, определяется тем, что при росте аргумента 0≤x1<x2 значение x2n>x1n возрастает на промежутке [0;+∞). При этом на промежутке (-∞;0] при росте аргумента 0≤-x2<-x1, значение также растет -x2n<-x1n, иначе x2n>x1n.
На следующем слайде выделено свойство 5 степенной функции с нечетным показателем степени, его описание. Указывается, что данное свойство следует из свойств 1-3 и для любого положительного x значение функции также будет положительным для всех натуральных n.
В конце презентации приведены примеры графиков степенной функции с нечетным натуральным показателем степени.

Презентация «Функция y=xn» дает подробное понятное описание свойств степенной функции, что позволяет ее использовать не только как наглядное пособие на уроках математики в школе, но и рекомендовать для самостоятельного изучения, а также применять при дистанционном обучении.
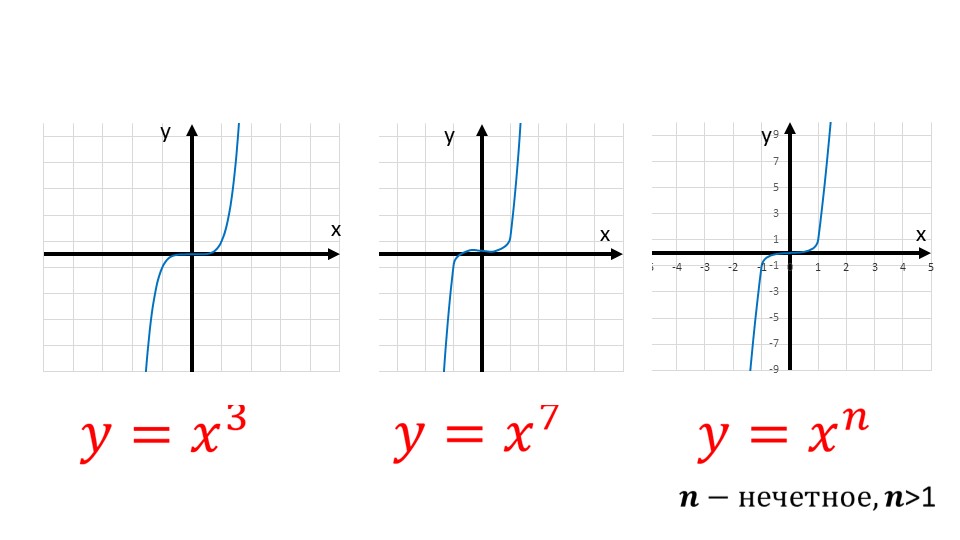
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8780 |
| Номер материала | 646 |