
Презентация "Функция y=sinx, ее свойства и график"

Краткое описание документа:
Раздел в математике тригонометрия включает в себя изучение таких понятий, как синус, косинус, тангенс и котангенс. В отдельности школьникам необходимо будет рассмотреть каждую функцию, изучить характер поведения на графике, рассмотреть периодичность, область определения, область значений и другие параметры.
Итак, функция синуса. На первом слайде выводится общий вид функции. В качестве аргумента используется переменная t.


Первым делом, как и при каждой функции, рассматривается область определения, которая указывает на то, какие значения может принимать аргумент. В случае синуса – это вся числовая ось. Увидеть это можно впоследствии на графике функции.

Второе свойство, которое рассматривается на примере синуса – это четность. Синусоид является нечетной. Это объясняется тем, что функция от –х будет равняться функции со знаком минус. Для того чтобы вспомнить данный материал, можно вернуться в предыдущие презентации и просмотреть.

Демонстрируется данное свойство на единичной окружности, которая появляется в левой стороне слайда. Таким образом, свойство доказывается и геометрически.
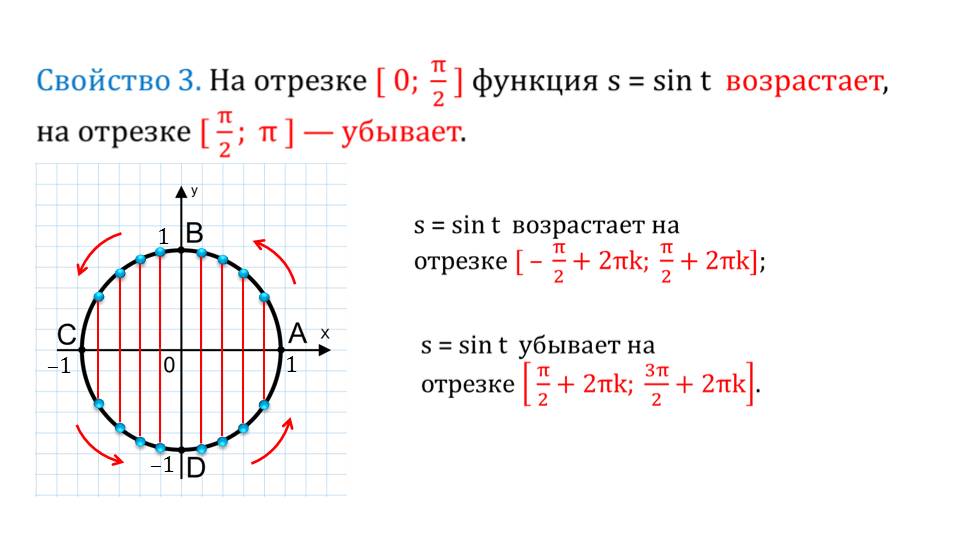
Третье свойство, которое необходимо также рассмотреть – это свойство монотонности. На некоторых отрезках функция возрастает, на некоторых – убывает. Это дает нам возможность назвать синусоиду монотонной функцией. Так как интервалов возрастания и убывания бесконечное число, отмечается это периодичностью.

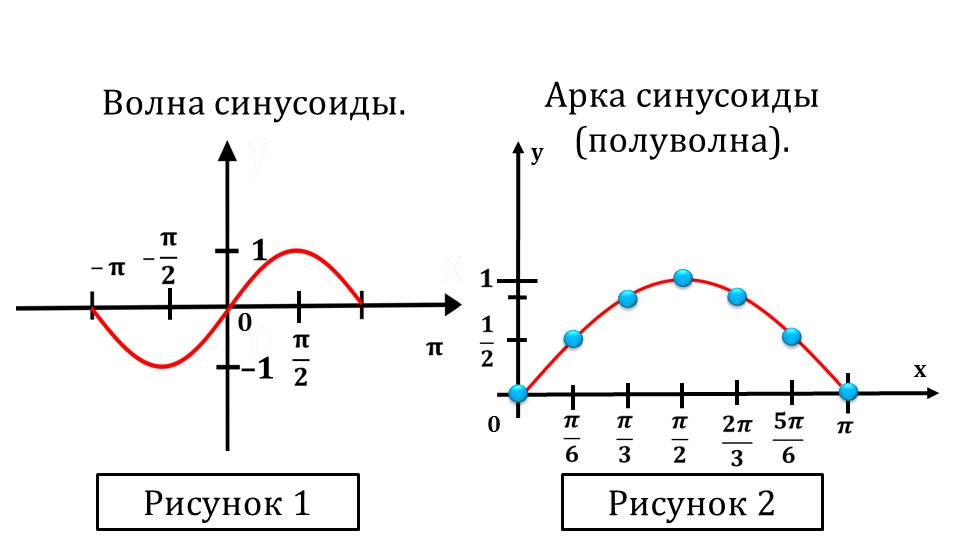
Четвертое свойство – ограниченность. Синусоида является ограниченной и сверху, и снизу. Минимальное значение, при этом, - 1, максимальное +1. Таким образом, функция синуса ограниченная и сверху, и снизу.
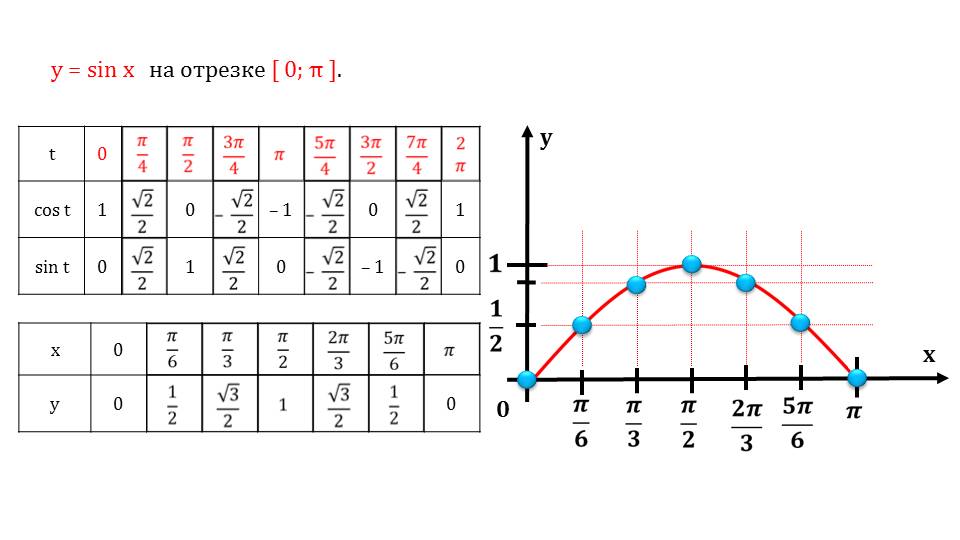
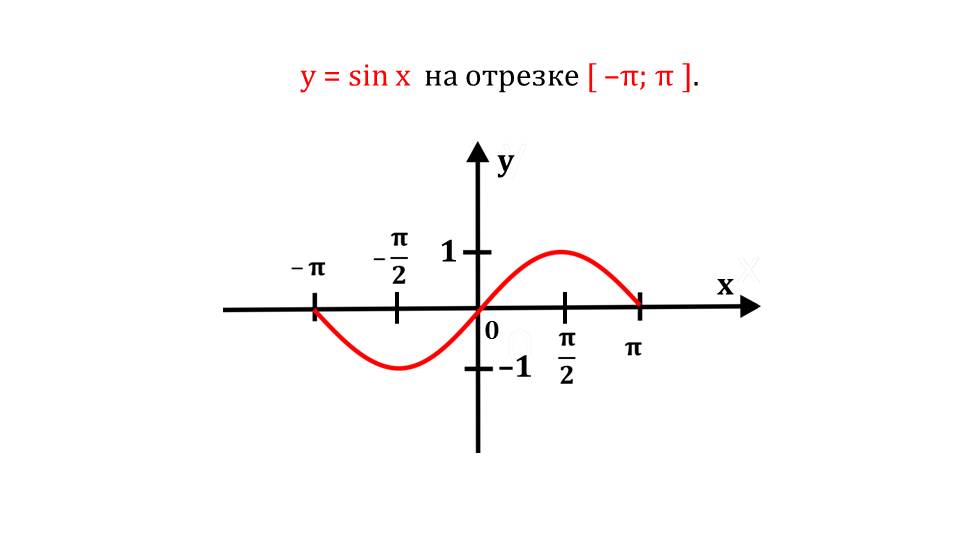
Далее рассматривается отдельный интервал синусоиды, прочерчивается поточечно график. После чего можно увидеть на графике более расширенный интервал – от минус Пи до Пи.
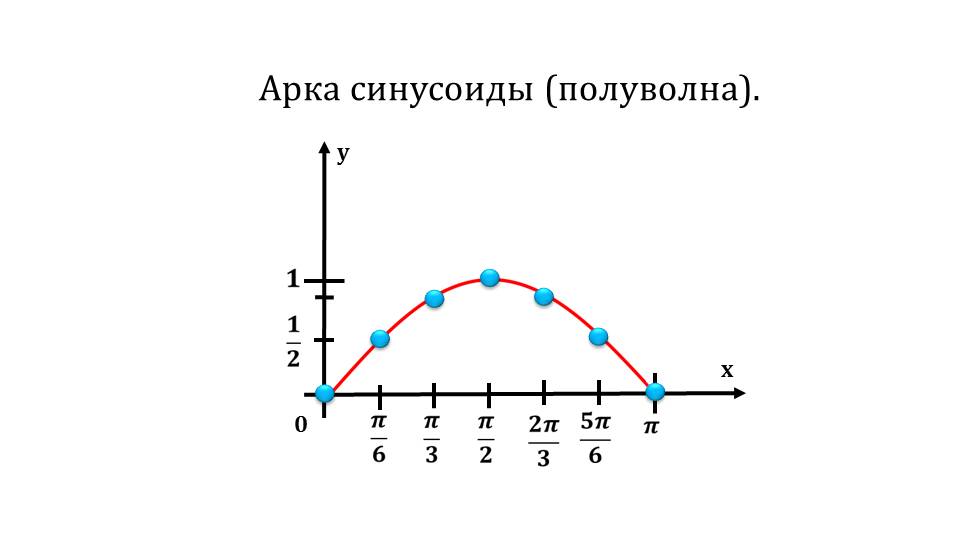

Дается определение синусоиды, которые необходимо заполнить. Далее рассматриваются различные деформации синусоиды при разных значениях.
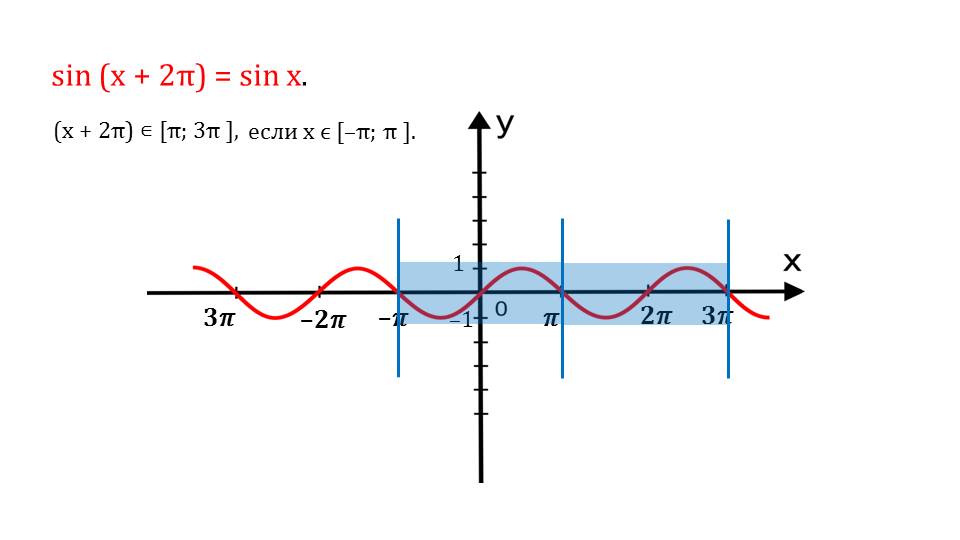
После того, как даны определение, продолжается рассматривание свойств функции синуса. Она является непрерывной. Это наглядно видно на графике функции. Никаких точек разрыва не существует.
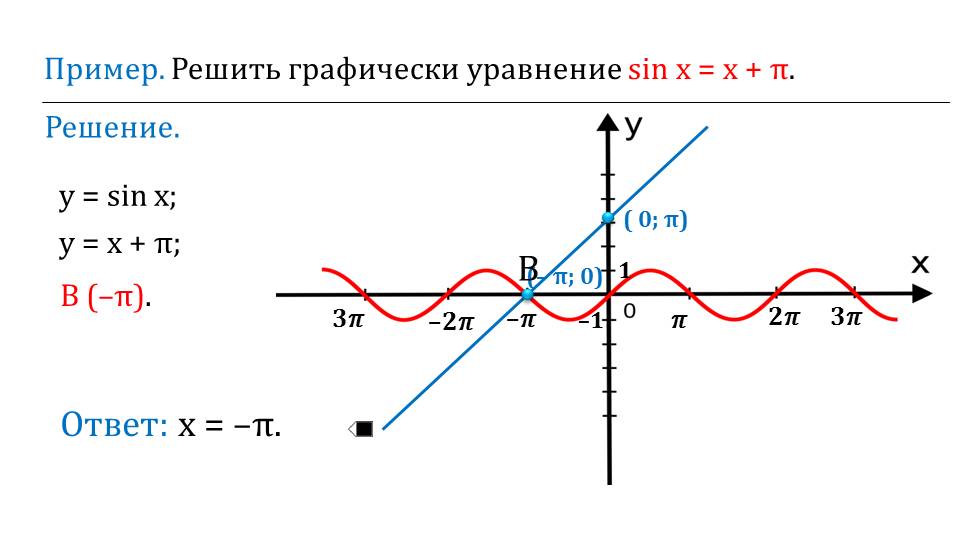
Последний слайд показывает, как графическим образом можно решить уравнение, в котором содержится функция синуса. Такой способ упростит решение и сделает его более наглядным.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7754 |
| Номер материала | 793 |