
Презентация "Исследование функции на монотонность"

Краткое описание документа:
Исследованию функций в курсе алгебры уделяется довольно много времени. Это связано с обилием материала, который направлен на изучение функций. Важное значение имеет исследование функции на монотонность. Данные знания и умения пригодятся и на других предметах. Чтобы тема была быстрее и качественней усвоена, можно применить на уроке данную презентацию, которую автор выполнил для упрощения работы учителя и экономии его времени.

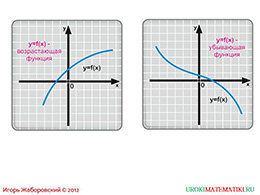
слайды 1-2 (Тема презентации "Исследование функции на монотонность", пример)
Начинается данная презентация с изображения графиков двух произвольных функций. Первый график демонстрирует функцию возрастающую, второй – убывающую.
Следующий слайд – текстовый. Здесь автор определяет понятия возрастающей и убывающей функций. Кроме самого определения каждого из видов функций, здесь имеется более удобная для запоминания формулировка, которая гласит, что если большему значению аргумента соответствует большее значение функции, то функция возрастает, а если большему значению аргумента соответствует меньшее значение функции, то функция убывает.

слайды 3-4 (примеры)
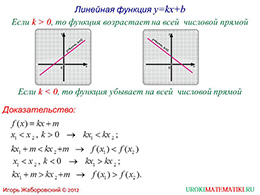
Далее автор презентации предлагает перейти непосредственно к конкретным функциям. И первая такая функция является линейной. В данном случае монотонность функции зависит от коэффициента k. если он положительный, то функция возрастает, если отрицательный, то – убывает. На этом же слайде автор приводит доказательство этих фактов, которое основывается на свойствах неравенств.
Далее, на следующем слайде автор отмечает, что если функция возрастает или убывает на всей своей области определения, то ее называют возрастающей или убывающей, при этом, не обязательно указывать промежутки. И тут же приводится пример линейной функции, которая возрастает на всей числовой прямой, а значит, функция, возрастающая на всей области определения.

слайды 5-6 (примеры)
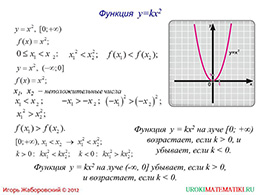
Затем рассмотрение данного материала переходит к квадратичной функции, вершина которой находится в начале координат. На этом слайде автор довольно подробно описывает, какие функция имеет промежутки возрастания и убывания. При этом все подробно расписывается и доказывается. Более того, автор для иллюстрации демонстрирует этот случай на рисунке.
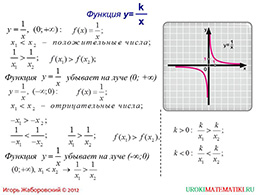
Аналогично предыдущему случаю, автор рассматривает следующую функцию, графиком которой является гипербола. Здесь также все подробно описано, доказываются все возможные случаи монотонности данного вида функций. Промежутки возрастания и убывания здесь зависят от коэффициента k. При положительном значении данного коэффициента функция убывает, а при отрицательном, наоборот, возрастает.

слайды 7-8 (примеры)
На следующем слайде рассмотрена функция, где присутствует квадратный корень. С помощью некоторых операций автор показывает, что данная функция всегда возрастает, то есть на всей области определения, при этом, не имея точек разрыва, как в предыдущем случае. Так автор приводит к понятию монотонности функции. Теперь самое время переходить к исследованию функции на монотонность.
Исследовать функцию на монотонность, означает найти промежутки возрастания и убывания функции. И это продемонстрировано в презентации на примере, где дана кусочная функция, заданная аналитически. Более того, в данном примере необходимо не просто указать промежутки монотонности, а полностью прочитать график, то есть описать его свойства. А в эти свойства как раз и будет входить пункт с указанием промежутков монотонности.
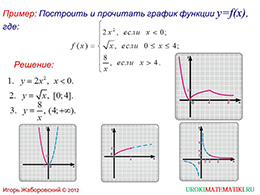
слайды 9-10 (пример)
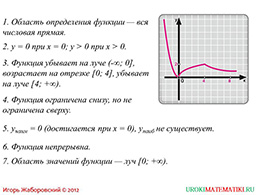
Эта функция представлена тремя разными функциями на определенных участках. Поэтому для начала требуется построить график этой функции, состоящий на разных участках из графиков определенных функций. В результате получается график той функции, которая задана в условии. Теперь можно описывать этот график. На последнем слайде представлены семь свойств этой функции, а третьим пунктом, как раз, указаны промежутки возрастания и убывания. Таким образом, функция исследована на монотонность.
Презентация подходит для урока изучения нового материала. При необходимости учитель может дополнить ее или немного изменить.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7324 |
| Номер материала | 313 |