
Урок "Свойства числовых неравенств". Часть 2

Краткое описание документа:
В предыдущем уроке были рассмотрены 6 основных свойств числовых неравенств. В дальнейшем школьники должны научиться их применять на практических примерах. Начинать надо с самого простого.
В данном видеоуроке будут рассмотрены практические примеры. Диктор подробно объяснит их решения, ссылаясь на основные свойства. Поэтому, прежде, чем перейти к изучению данного видеоурока, необходимо просмотреть предыдущий и подробно его изучить.
Первый пример, который рассматривается в видеоуроке представляет собой следующее: имеется две дроби с одинаковыми числителями, равными единице, в знаменателе имеются разные значение, положительные a и b. Между ними стоит знак «меньше». Необходимо доказать, что знак поставлен верно, при этом, зная некоторые дополнительные условия.
Итак, по условию разность этих дробей с числителями единица равняется дроби, в числителей, которой разность знаменателей, а в знаменателе – их произведение.
Далее начинается рассматривание доказательства. При этом ,как видим, диктор ссылается на свойства числовых неравенств.
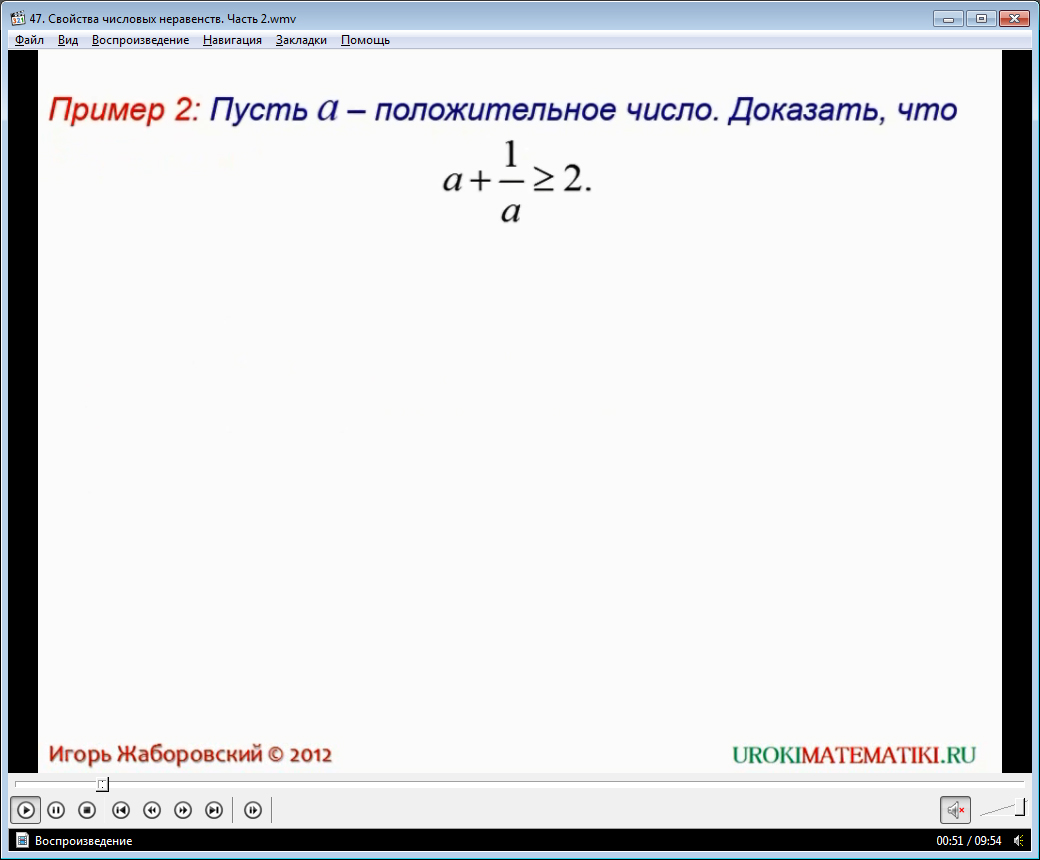
Второй пример является более интересный. Необходимо доказать, что сумма некоторого значения с его обратным значением, то есть дробью с числителем, равным 1, и знаменателем, равным данному изначально заданному значению, является больше либо равно двум.
Приводится подробное решение-доказательство.
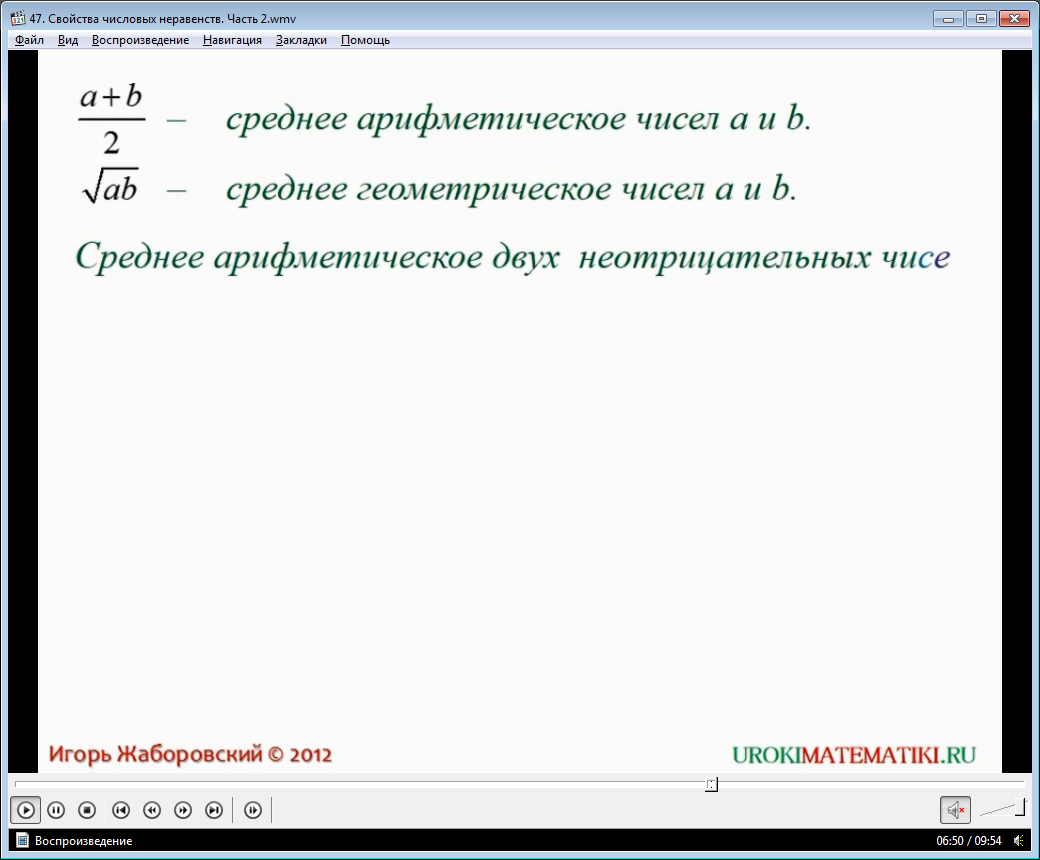
После того, как приводятся еще два примера, на экран выводятся формулы среднего арифметического и среднего геометрического двух значений. Стоит знать, что первое либо больше, либо равно среднего геометрического всегда.
Если записать данное утверждение в виде неравенства, то получим неравенство Коши. Оно доказывается визуально с помощью некоторых построений.
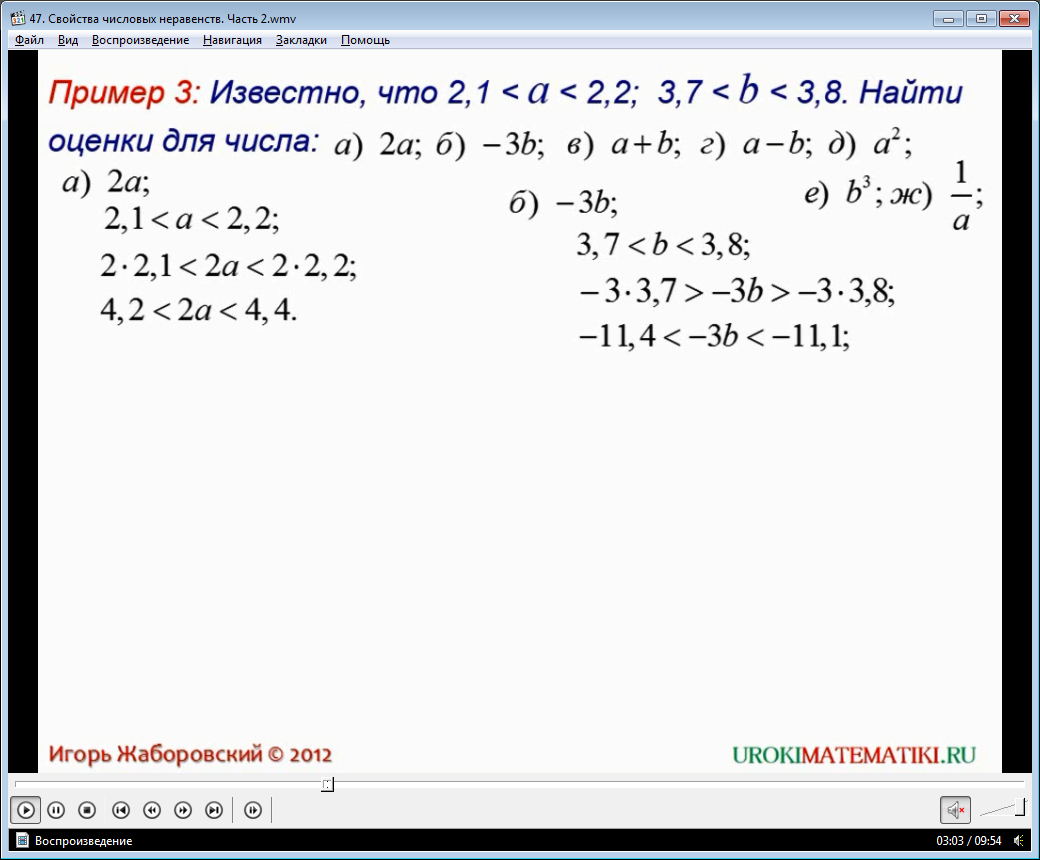
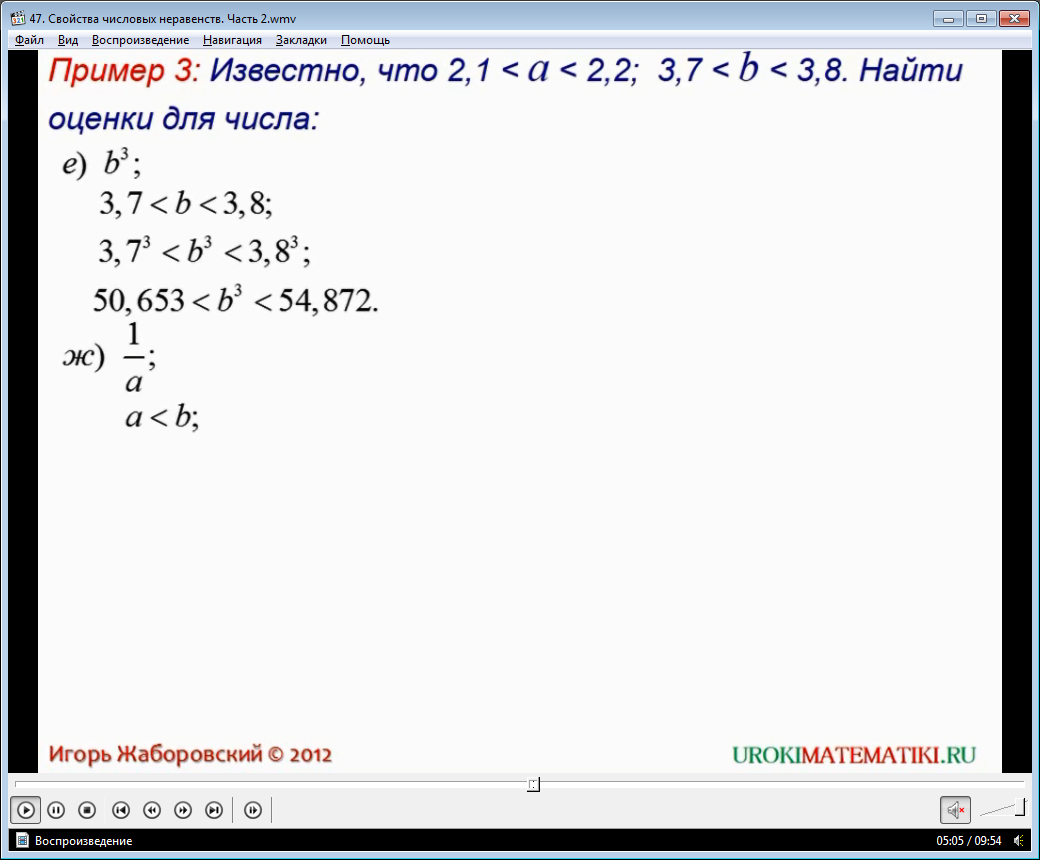
И, наконец, в конце видеоурока рассматривается последний пример, который состоит из ряда пунктов. Необходимо сравнить различные значения. К каждому пункту приводятся решения.
С помощью данного видеоурока можно провести интересный практический урок. Школьникам будут понятные принципы решения тех или иных числовых неравенств. Примеры, которые приводятся в видеоуроке, можно задать в качестве домашнего задания, либо самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4440 |
| Номер материала | 569 |