
Презентация "Изучение графика числовых функций"

Краткое описание документа:
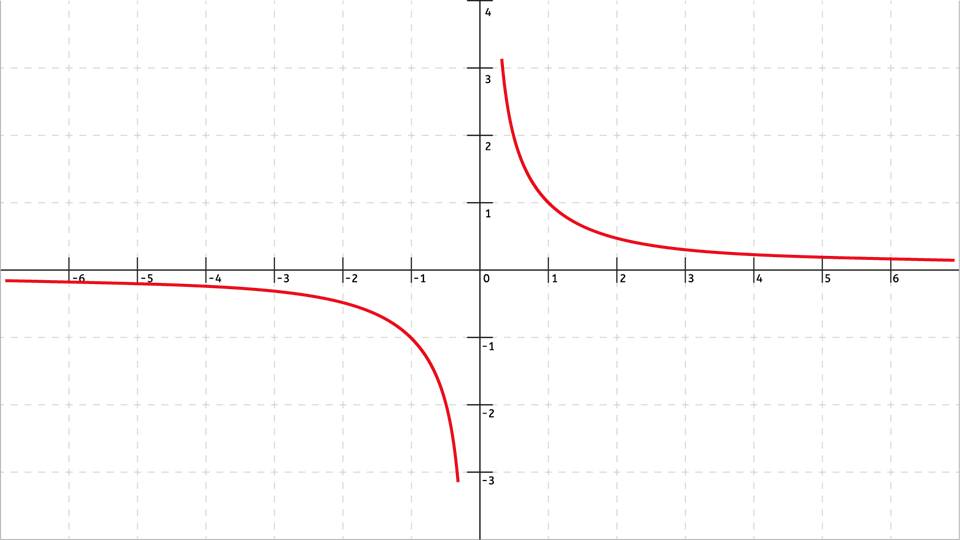
Данная презентация предназначена для 10-классников, которые изучают тему «Чтение графика числовых функций». На первом слайде мы видим график некоторой функции в масштабе.
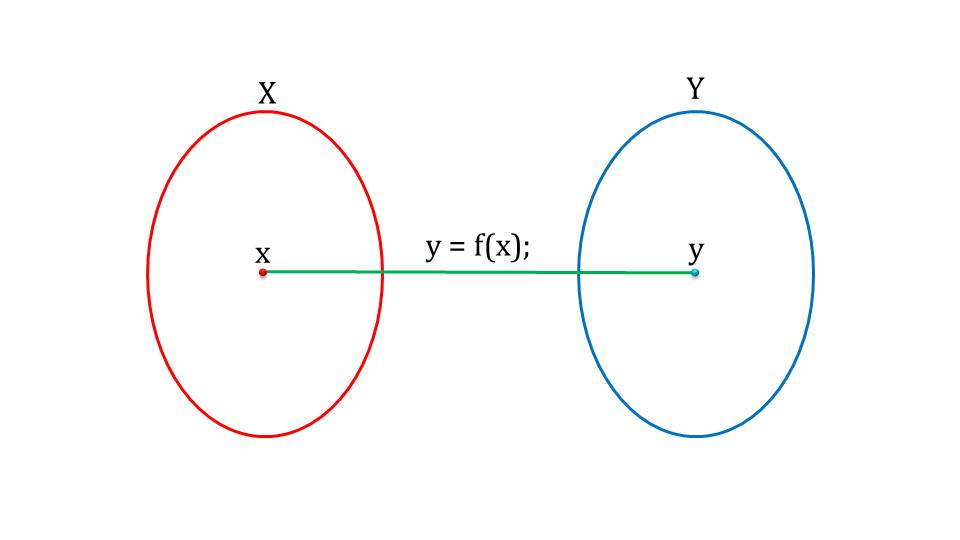
Далее изображается уже знакомая нам схема, на которой мы видим: слева область определения, графически обозначенное овалом, справа – область значений. Если выбрать некоторое значения из области аргументов, то, с использованием некоторого правила, которое задается функцией, можно найти значение из области Y-ов, то есть области значений.
Множество все х-ов называется множеством определений, всех у-ов – множеством значений. Как это обозначается, школьники уже знают.


Если записать функцию в виде равенства y=f(x), то будем называть это уравнением функции. При этом, х является независимой переменной, также ее называют, как известно, аргументом функции. А у считается зависимой переменной. Ведь мы задаем некоторый х из области определения, и по определенному правилу мы находим у. получается, что у зависит от х.


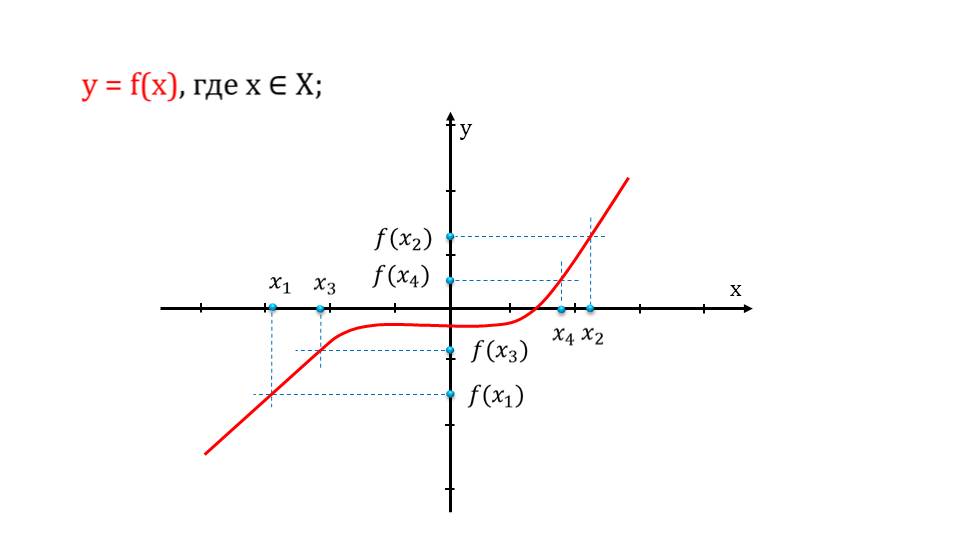
На следующем слайде приводится график некоторой функции f(x). На котором мы видим, как можно определить зависимость х от у на графике, и как можно найти одно, зная другое. Для этого проводится параллельная прямая оси ох и оу через искомую точку.
Что же такое график функции? На 9 слайде дается определение. Несмотря на то, что с графиком уже давно имели дело, все же, не помешает вспомнить формулировку определения. График представляет совокупность точек, которые удовлетворяют области определения и области значений.

Свойства функции рассматриваются далее на следующем слайде. Стоит отметить, что есть свойства, которыми обладают не все функции. Например, это непрерывность, четность и нечетность, ограниченность, вогнутость и выпуклость. Иными словами функция может не быть одновременно ни четной, ни нечетной, ни вогнутой и ни выпуклой и т.д.


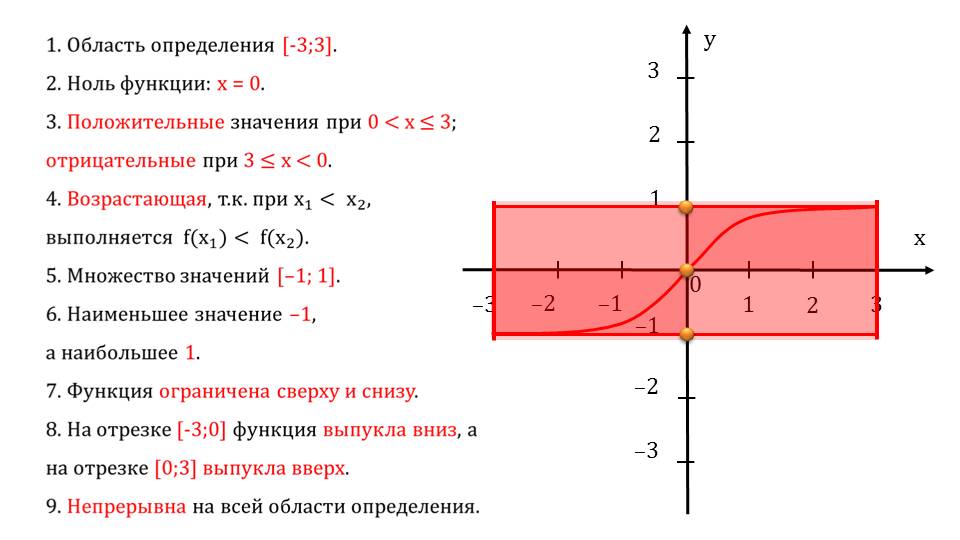
Далее приводится анализ на изучение свойства графика рациональной функции. Находятся область определения, нули функции область возрастания, ограниченность, наибольшее и наименьшее значение, область непрерывности. Приводится также график для наглядности.

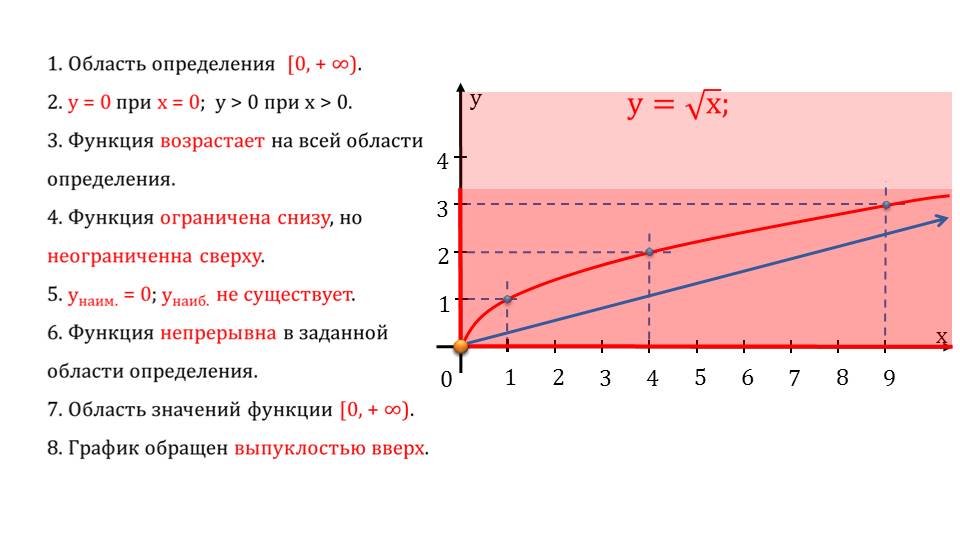
После этого рассматривается еще один график функции по 9 пунктам. С помощью специальных анимационных эффектов все они демонстрируются на графике.
Данная тема требует много внимания и усидчивости. Необходимо решать множество примеров, рассматривать различные графики, чтобы как можно полноценно понять тему. Не стоит останавливаться на теории.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 2848 |
| Номер материала | 780 |