
Презентация "Конус"

Краткое описание документа:
Презентация «Конус» помогает рассмотреть на уроке геометрии еще одно тело вращения – конус. Особенность уроков по данной теме такая же, как и других тем по стереометрии – сложности при построении объемных фигур. Если требуется строить объемную фигуру на доске, то искажения ручного построения могут помешать правильно воспринимать материал учащимися. В этом случае создание презентации по теме избавляет от характерных проблем. Учителю легче обеспечить наглядное представление и понимание материала. Презентация охватывает этапы объяснения новой темы, детально и понятно описывая, а также выделяя важные моменты. В нее включено понятие конуса, определение, формула нахождения объема и развернутое объяснение нахождения площади боковой поверхности конуса.

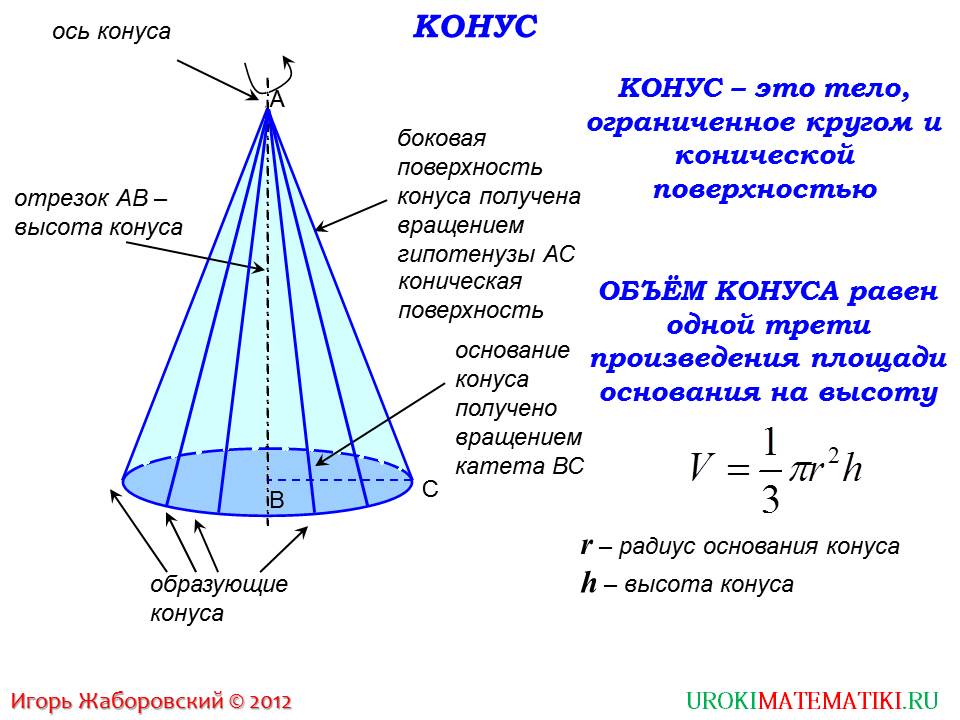
В презентации используется анимированное изображение, которое помогает понять особенности образования фигуры вращения, наглядно представить развертку боковой поверхности. Выделение текста цветом побуждает обратить особое внимание на формулировки.
После ознакомления с темой презентации учащиеся переходят к общему представлению данного геометрического тела. На слайде изображается прямоугольный треугольник, с которого начинается построение тела вращения – конуса. Вращаясь вокруг одного их катетов, треугольник образует данное геометрическое тело. Основная фигура и способ образования конуса определяют его свойства. Созданная на рисунке модель конуса раскладывается на составляющие. Каждая часть описывается словесно, чтобы облегчить запоминание. Катет, вокруг которого вращался прямоугольный треугольник, становится осью вращения конуса. Отрезок, сопоставленный данному катету, будет являться высотой конуса. Линии, соответствующие гипотенузе треугольника, в любой части конуса будут представлять собой образующие. Основание – круг, который образован вращением стороны ВС, второго катета треугольника. Учителем выделяется боковая коническая поверхность конуса, круг основания, которые часто являются предметом изучения при решении геометрических задач. Справа от конуса дается определение его как тела, ограниченного конической поверхностью и кругом. Ниже располагается формула нахождения объема конуса . В ней используются уже рассмотренные части конуса – радиус, высота. Формулировка выделена синим цветом, что облегчает ее запоминание.
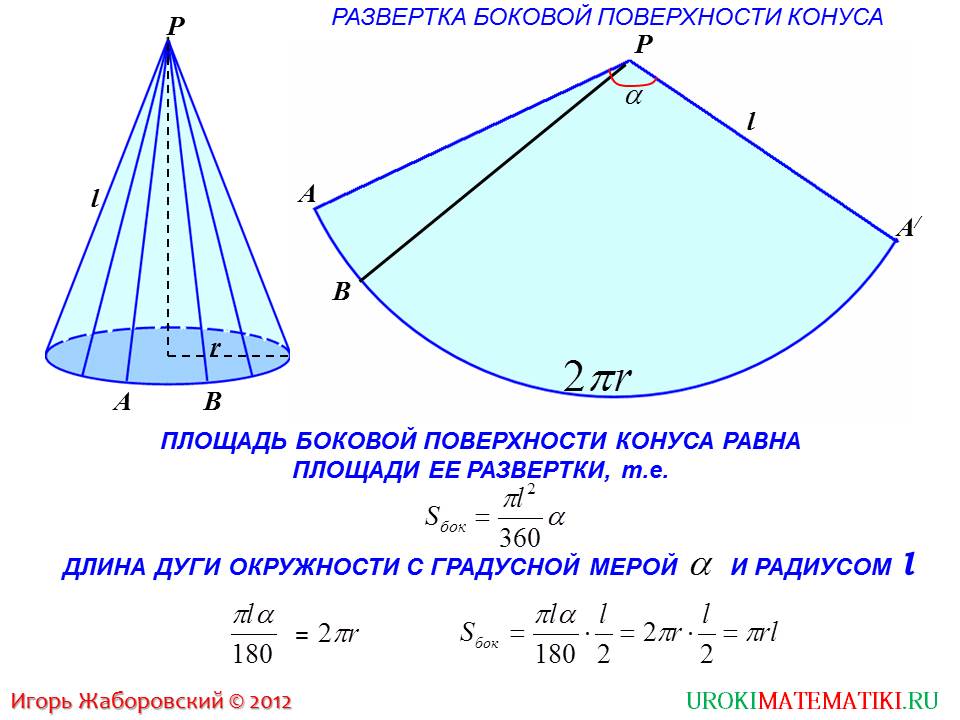
Второй слайд содержит информацию о развертке боковой поверхности конуса. Рассматриваемый конус разрезается образующей РА. Боковая поверхность конуса представляет собой сектор АРА’ с дугой , а радиусом l. Чтобы найти площадь боковой поверхности конуса, используется формула для нахождения площади развертки. Сектор развертки построен на углу с радиусом l. Длина дуги будет равна . Она одновременно равна и длине окружности круга основания . Подставив данное выражение в формулу, получаем = .
Презентация доступно раскрывает понятие конуса и его свойств, дает представление о нахождении важных характеристик конуса – площади боковой поверхности и объеме. Поэтому, кроме урока геометрии, для наглядности она может быть использована при дистанционном обучении. Также может быть полезной ученикам для самостоятельного изучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6324 |
| Номер материала | 732 |