
Презентация "Применение векторов к решению задач"

Краткое описание документа:
Тема «Векторы» сама по себе в курсе геометрии школьного курса занимает довольно мало места. Но ее применение имеет очень большое значение. Ведь чтобы решить некоторые задачи, требуется знание операций над векторами и умение их построить. Особенно это касается такой науки, как физики. Также подобные задания имеются в итоговых аттестационных работах. Значит изучение данной темы крайне важно. Но прежде, чем приступить к уроку по теме «Применение векторов к решению задач», необходимо получить определенный объем знаний по теме «Векторы». Тогда можно будет легко применить эти знания при решении разного рода задач, требующие знание векторов.

слайды 1-2 (Тема презентации "Применение векторов к решению задач", пример)
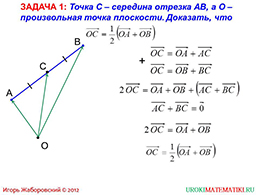
В данной презентации рассматривается лишь два примера, когда можно применять знания по векторам. И первый пример на первый взгляд сразу говорит о том, что придется вспомнить о векторах некоторые моменты. Здесь всего лишь требуется доказать равенство, если известно, что некоторая точка C является серединой отрезка AB, а точка O – произвольная точка плоскости. К данному условию на слайде презентации имеется иллюстрация, которая поможет осуществить доказательство.
Для доказательство равенства изначально применяются умения складывать векторы. То есть по чертежу обучающиеся должны уметь определять, какой вектор является суммой других векторов. Эту взаимосвязь автор выражает в двух выражениях. Где он двумя разными равенствами определяет один и тот же вектор. Затем эти два равенства складываются, применяя некоторые свойства векторов, выполняются некоторые преобразования и в результате получается то, что требовалось доказать. Все довольно подробно описывается на математическом языке, что, в свою очередь, формирует у обучающихся математическую грамотность.
Второй же пример совершенно никаким образом не связан с векторами. Конечно, данную задачу можно решить и без векторов. Но автор показывает, что бывают ситуации, которые проще и быстрее решаются именно с помощью знаний о векторах. Так получается и в данном случае.
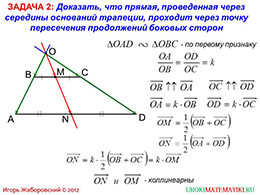
Требуется доказать, что прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон. И автор начинает рассмотрение доказательства на основе подобия треугольников.
Далее записано соотношение сторон подобных треугольников, и на этом начинается использование векторов. Берутся две пары одинаково направленных векторов, исходящих из одной и той же точки, которая является точкой пересечения боковых сторон трапеции.
Далее применяется произведение вектора на число и некоторые другие действия и свойства. В конечном итоге получается, что векторы, которые образуют основания трапеции коллинеарные. А это значит, что основания параллельны. Поэтому все легко доказано с применением знаний векторов.
слайд 3 (пример)
Но так как векторы изучаются в конце восьмого класс, а также в девятом, то и применение подобных знаний возможно после некоторого полученного объема знаний. Поэтому применять знания по теме «Векторы» можно будет начиная с конца восьмого класса. Но более интересные задачи с применением векторов можно встретить в физике.
На уроке по теме «Применение векторов в решении задач» может применяться данная презентация в оригинальном виде или в доработанном, если учитель решить добавить какие-то свои примеры. Хорошо подойдет данная презентация для какого-то тематического внеклассного занятия, например на неделе математики, но с добавлением интересных примеров и фактов, которые связаны с подобной тематикой.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8477 |
| Номер материала | 364 |