
Урок "Применение векторов к решению задач"

Краткое описание документа:
Не всегда задачи можно решать традиционными способами. Не всех полученных знаний достаточно для того, чтобы решить какую-то определенную задачу. И не все способы решения задач одинаково легки. Поэтому во время решения задач рекомендуется использовать тот способ, который более рационален и проще.
Иногда использование знаний о векторах, а также умений и навыков построения векторов, их суммы и вычитания помогают решить некоторые задачи быстрее и легче, чем с использованием каких-то других методов. С помощью векторов доказываются многие теоремы. Поэтому автор данного урока предлагает научиться решать задачи с помощью векторов. Для этого он и разработал этот видеоурок.

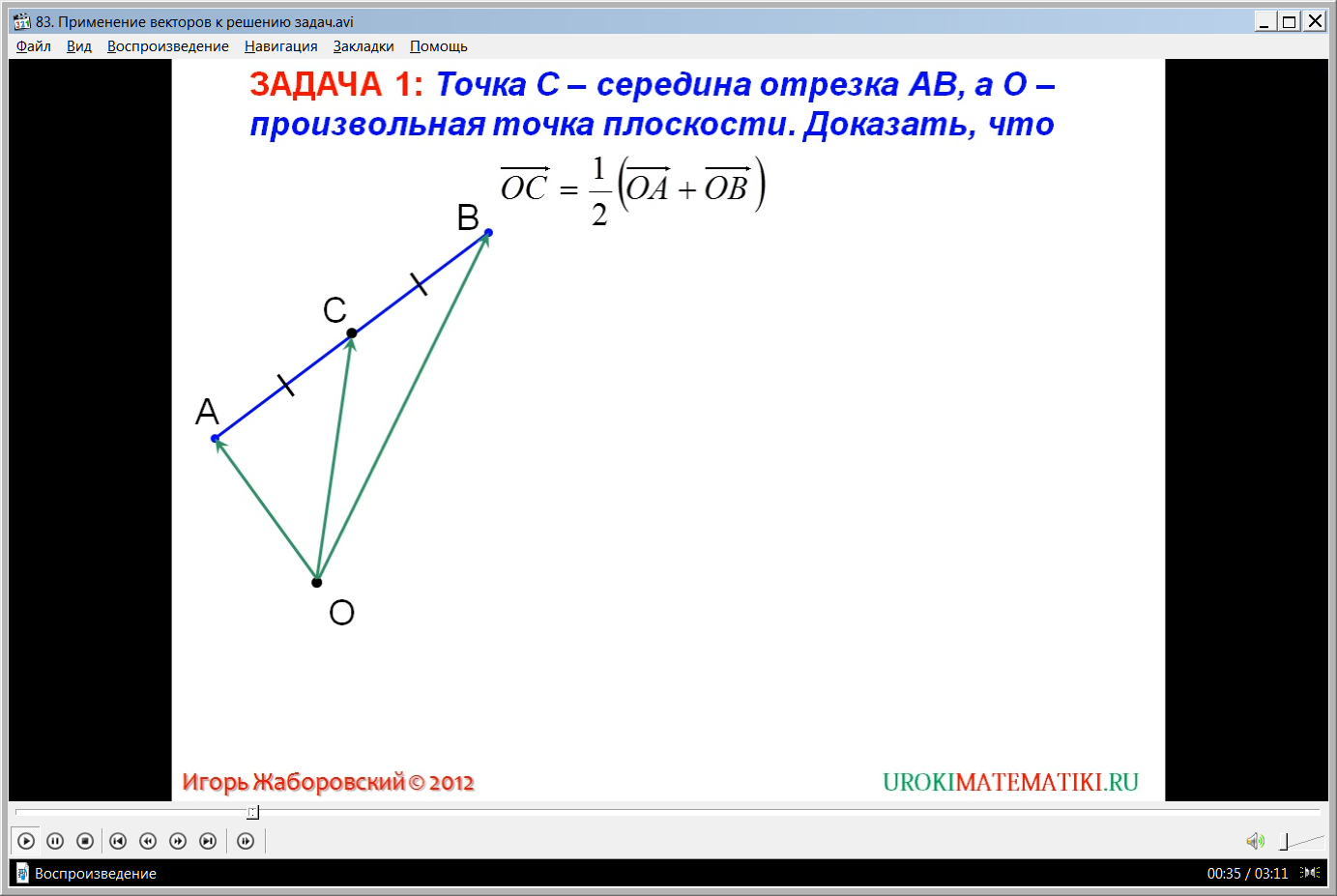
Видеоурок занимает 3:12 минут общего времени обыкновенного урока. Начинается урок с рассмотрения примеров. Первая задача – на доказательство. На основании тех знаний, которые обучающиеся получали на протяжении всего времени, когда изучалась тема «Векторы», строится доказательство в данной задаче. По ходу доказательства автор строит чертеж. На этом чертеже не последнюю роль играют векторы. Хотя по условию задачи речь шла об отрезке и о равенстве, содержащем векторы.
По построенному чертежу автор ведет рассуждение. Параллельно ведутся записи, которые являются ключевыми в доказательстве. Пригодились и знания по нахождению суммы векторов. Эта задача успешно решена и доказана.
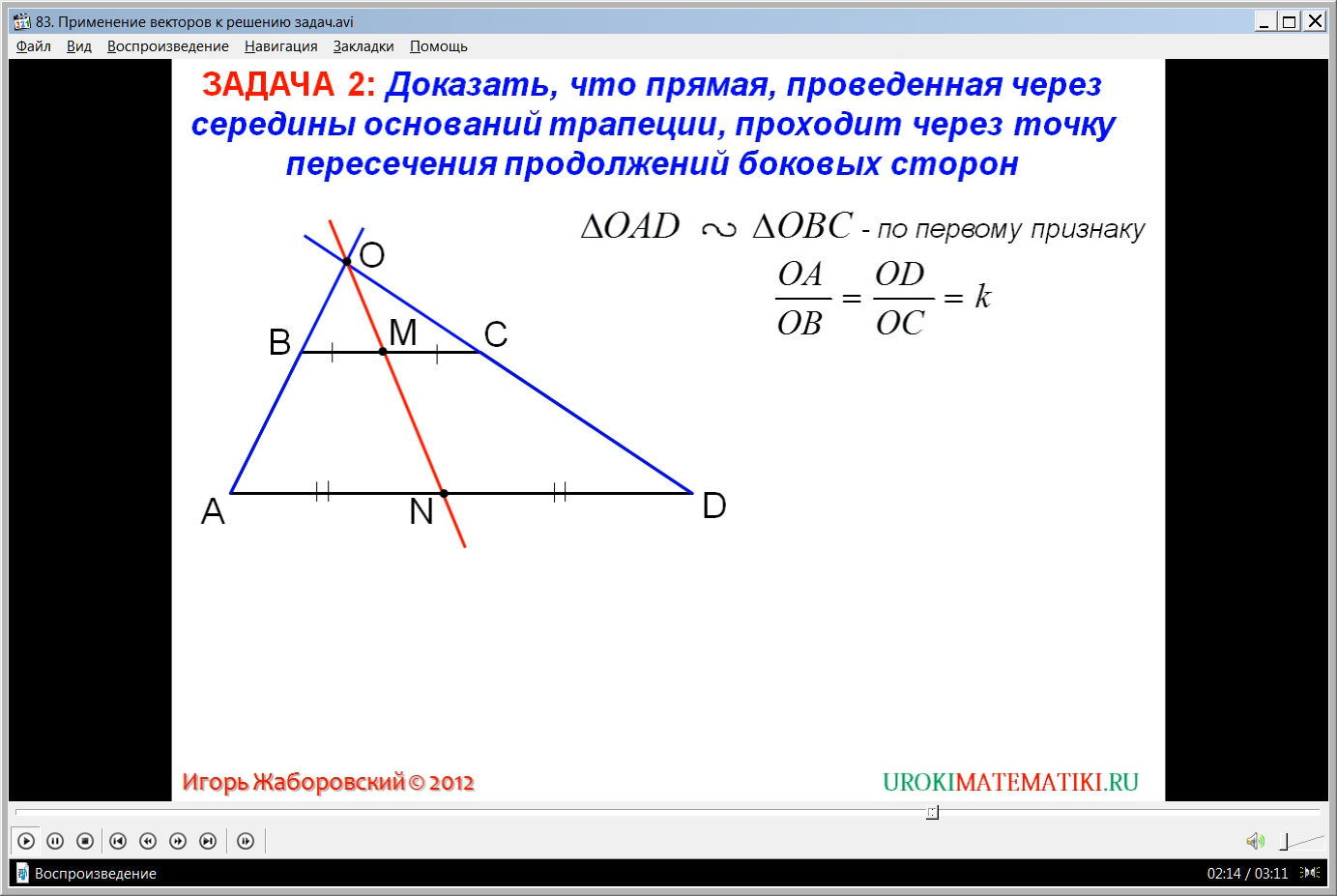
Следующий пример, который рассматривает автор урока, совершенно никаким образом не затрагивает векторы. Но это только на первый взгляд. Да, в формулировке нет фраз, которые касались бы векторов. Но доказательство строится на основании знаний, полученных на уроках по теме «Векторы». Чтобы доказательство было легко осуществить, автор строит чертеж по условию задачи. Далее он прибегает к методу дополнения чертежа элементами, путем достроения. И уже по готовому чертежу с имеющимися знаниями ведется доказательство. Одновременно с этим автор записывает все действия подробно. В этой задаче оказались полезными знания о сонаправленных векторах, понятие произведения вектора на число и суммы векторов.

Так на основании двух примеров автор показал, что даже не связанные с векторами задачи, могут решаться с их помощью. Остальное за учителем. Ему необходимо подобрать задачи, в которых могут пригодиться знания векторов, но имеющие и другие способы решения. Так обучающиеся смогут понять, что какой способ рациональнее и проще.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7108 |
| Номер материала | 621 |