
Презентация "Координаты вектора"

Краткое описание документа:
Презентация «Координаты вектора» - мультимедийное пособие, которое может сопровождать объяснение девятиклассникам правил проведения операций над векторами, а также формировать умение находить результирующий вектор при сложении, вычитании и умножении на число различных векторов.
Предварительно учащимися была изучена тема разложения вектора по двум неколлинеарным векторам. После освоения этой темы они уже получили навыки в разложении вектора по двум неколлинеарным векторам. После повторения знаний по данной теме можно приступать к изучению операций над векторами. Для этого необходимо уяснить, что такое координаты вектора, как образуется сумма двух векторов и что она собой представляет, разность и умножение вектора на число. В данной презентации охватывается объяснение всех этих этапов изучения темы, а также закрепление приобретенных знаний решением примера.

В презентации используется анимация, которая помогает учителю обеспечить наглядность в построении векторов, облегчая понимание материала учениками. Разные векторы при построении, а также формулировка правил выделяются цветом, чтобы ученикам легче было разобраться в построении результирующего вектора, запомнить утверждения.
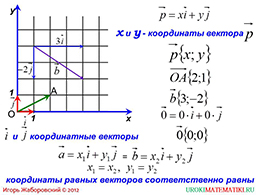
Презентация начинается с демонстрации системы координат, обозначения на ней единичных векторов с началом в точке отсчета. По ходу объяснения отмечается, что вектор так же, как раскладывается по любым двум неколлинеарным векторам, может быть разложен по единичным векторам i ⃗ и j ⃗. Они в слайде обозначены как координатные векторы. Соответственно в выражении, которое отображает вектор p ⃗, разложенный по данным координатным векторам, значения x и y, коэффициенты разложения, являются координатами вектора p ⃗. Ниже на слайде вводится обозначение вектора через его координаты, которые в дальнейшем ученики будут использовать при записи. Рассматриваются примеры векторов (OA) ⃗ и b ⃗, описанные при помощи координат вектора. Далее рассматриваются свойства векторов, выраженные через их координаты. Демонстрируется обозначение вектора с нулевыми координатами. Далее рассматриваются свойства векторов с одинаковыми координатами. Два вектора a ⃗ и b ⃗, разложенные по единичным векторам, характеризуются координатами x и y. Если данные соответствующие координаты попарно равны, то и эти векторы будут равными.
Следующий слайд демонстрирует правило образования суммы векторов. Отмечается, что сумма двух векторов – это вектор.


В начале слайда формулируется правило образования суммы двух векторов, выделенное синим цветом. Рассматривается в общем виде сумма векторов a ⃗ и b ⃗. Демонстрируется обозначение векторов через их координаты, соответствующее им разложение по единичным векторам. Ниже рассматривается сумма векторов, которая характеризуется суммой выражений, являющихся разложением каждого вектора по единичным векторам. После группировки элементов суммы, можно наблюдать, как образуется суммарный вектор. Можно увидеть, что его координаты представляют собой попарные суммы соответствующих координат. Ниже демонстрируется обозначение суммарного вектора a ⃗+b ⃗ через координаты, представляющие собой суммы соответствующих координат.
На четвертом слайде демонстрируется образование разности векторов. Сначала формулируется правило, согласно которому формируется результирующий вектор разности двух векторов. Утверждается, что каждая координата разности представляется собой разность соответствующих координат исходных векторов. Ниже демонстрируется, как формируется разность, на примере двух векторов a ⃗ и b ⃗, представленных в виде, разложенных по единичным координатам. Ниже располагаются векторы a ⃗ и b ⃗, обозначенные через их координаты, что соответствует выражениям, которые представляют собой разложение вектора по единичным векторам. Чтобы получить разность векторов, выражение из вектора a ⃗, разложенного по единичным векторам, вычитается выражение разложения по единичным векторам, соответствующее вектору b ⃗. Соответствующие выражения вычитаются. После группировки значений и вынесения векторов i ⃗ и j ⃗ за скобки, получается результирующий вектор. Учащиеся могут наблюдать, что разность векторов представляет собой выражение, которое содержит соответствующие координаты в виде разности координат исходных векторов.
Третье свойство координат векторов свидетельствует о том, что при умножении вектора на число, получается вектор, в котором в результирующем выражении умножается каждая координата исходного вектора на это число. Рассматривается данное свойство в общем виде при помощи вектора a ⃗. Демонстрируется вектор, обозначенный при помощи координат x и y. После умножения вектора на число, в выражении, соответствующем данному вектору, коэффициент умножается на оба слагаемых выражения. Результирующий вектор выражается через координаты, которые образуются умножением на данное число.

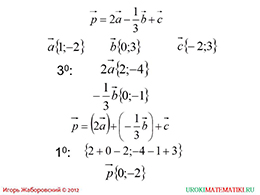
После общего представления правил операций над векторами рассматривается пример, в котором необходимо умение использовать все эти правила. Результирующий вектор p определяется после проведения умножения вектора на число, вычисления разности и суммы векторов. Данный пример помогает сформировать умение проводить операции над векторами, выраженными при помощи координат. Даются векторы a ⃗, b ⃗, c ⃗ с определенными координатами. Сначала определяются векторы, которые образуются умножением данных векторов на число. Разность и сумма векторов выражается в разности и сумме соответствующих координат векторов. Ответом примера является вектор, который образуется после проведения операций.
Данная презентация хорошо раскрывает порядок применения правил проведения операций над векторами, разложенными по координатам, формирует умение использовать данные правила при решении задач на векторы. Подробное и понятное объяснение может быть использовано не только на уроке в школе, но и при самостоятельном изучении, для дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6409 |
| Номер материала | 693 |