
Презентация "Квадратный трехчлен"

Краткое описание документа:
Презентация «Квадратный трехчлен» помогает сформировать у учеников стойкое понимание отличияквадратного трехчлена среди других многочленов, навыки оперировать введенными понятиями, а такжеуметь преобразовывать квадратный трехчлен, используя изученные способы и применять данные умениядля решения практических задач.
Тема является продолжением изученного материала, закрепляет умение раскладывать многочлены намножители, но выделяет важную часть многочленов - квадратный трехчлен. Она требует от ученикаполной концентрации внимания, хорошего запоминания материала. Особенно важно умение выделятьизученные конструкции. Учащемуся необходимо легко отличать квадратный трехчлен от другихмногочленов, автоматически использовать известные методы для разложения его на множители. Поэтомувыбран способ подачи материала при помощи презентации, которая не содержит отвлекающих эффектов,а просто и понятно раскрывает содержание основных понятий, подает их в форме, наиболее удобной длявосприятия и запоминания. Использование различных цветов помогает выделить изучаемые понятия,обозначить математическую запись, чтобы облегчить ее запоминание.


слайды 1-2 (Тема презентации "Квадратный трехчлен", примеры)
Начинается презентация с определения квадратного трехчлена. Вводится понятие на примерах сразличными знаками и содержанием разного количества одночленов, чтобы ученик мог узнать квадратныйтрехчлен в любой вариации. Далее понятие представляется в общем виде и производится логичныйпереход к определению понятия.

слайды 3-4 (определение квадратного трехчлена)
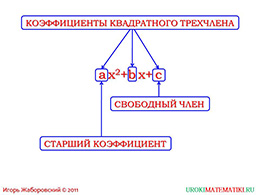
Следующий слайд формирует навык воспроизводить определение. Такой способ является наиболееоптимальным для запоминания материала. Название выделено красным, алгебраическая запись – синимцветом. Далее уточняется название членов квадратного трехчлена. Трехчлен разложен при помощи схемы,важность данного уточнения подчеркивается выделением красным цветом, так как далее ученику придетсяупотреблять названия постоянно при решении задач с использованием квадратного трехчлена.


слайды 5-6 (примеры)
На следующем слайде рассматриваются частные случаи, к общему виду с выделением названных членовприводятся квадратные трехчлены разного вида. Уточняется полный вид квадратного трехчлена сосвободным членом, равным нулю. Также уточняется, что отсутствие множителя перед переменной хозначает в качестве множителя единицу. Ученику подается общий вид приведенного квадратноготрехчлена с указанием старшего коэффициента, равного единице. Следующие три примера знакомят сособенностями преобразования квадратного трехчлена к произведению выражений.
На шестом слайде рассматривается первый пример, где требуется выделить квадрат разности вквадратном трехчлене, где старший член равен 1. Пример помогает закрепить навыки преобразованиявыражений, используя дополнение выражения членами, которые не меняют его значения. Средний члентрехчлена раскладывают на множители, приводя конструкцию к виду удвоенного произведения,содержащего переменную в первой степени. Становится понятным, какое число нужно прибавить ивычесть из выражения, чтобы использовать формулу разложения квадрата разности. Введенные ввыражение дополнительные члены помогают привести его к желаемому виду, вспомнив формулу квадратаразности. В качестве выражения за скобками демонстрируется число, являющееся результатомостаточных вычислений. Таким образом, закрепляются умения использовать введение дополнительныхчисел для решения задач, а также определяются особенности использования данного способа длярешения заданий с квадратным трехчленом.


слайды 7-8 (примеры)
Во втором примере рассматривается еще один нюанс преобразования квадратного трехчлена со старшимкоэффициентом 1. Для того, чтобы получить удвоенное произведение для среднего члена, необходимовключить в число множителей дробь. Далее, подобным образом используя прибавление и отнимание одногои того же числа, можно так сгруппировать члены трехчлена, что получится вид разложенного квадратасуммы. В итоге получается выражение, являющееся суммой квадрата выражения в скобках и остаточногочислового значения.
Далее в примере 3 рассматривается разложение квадратного трехчлена на множители. Применяя тот жеприем прибавления и отнимания одного и того же числа, в итоге получаем разность квадратов. Далее,используя соответствующую формулу сокращенного умножения, выражение легко преобразуется к видупроизведения двух выражений.


слайды 9-10 (пример, калькулятор)
В примере 4 для того, чтобы использовать при решении формулы сокращенного умножения, нужнопривести квадратный трехчлен к виду, где старший член – 1. Для этого 3, старший член неприведенноговыражения, выносится за скобки. Выражение в скобках вышеизложенными способами (вводится ивыводится одно и то же число, а затем члены выражения группируются) приводится к виду разностиквадратов, что позволяет затем легко его преобразовать в произведение двух выражений, внесямножитель 3 под одну из скобок.
Последний пример рассматривает приложений полученных навыков при решении геометрических задач.Задачу с поиском наибольшего значения можно отнести к заданиям углубленного уровня, однако учительдемонстрирует простое решение такой задачи, используя полученные навыки. Предлагается в качествеспособа решения задачи подобного типа использовать составление выражения, описывающего нахождениеплощади прямоугольника, взяв одну из его сторон за неизвестное х. Составленное выражениепреобразуется к форме, в которой хорошо прослеживается тенденция, что с ростом размера стороны до 4см значение площади будет увеличиваться, после 4 см до 8 см оно будет уменьшаться, а более 8 см неимеет практического значения. Таким образом, данным способом легко произвести анализ и сделатьсоответствующий вывод.
Таким образом презентацией охватывается большая часть задач, поставленных перед учителем во времяизучения темы. Используемые в презентации приемы позволяют эффективно донести до ученика знания инавыки начального уровня и постепенно подвести его к освоению приемов решения интегрированных задачуглубленного уровня. Наиболее целесообразно использовать презентацию «Квадратный трехчлен» дляповышения уровня освоения изучаемого материала учеником на уроке и для дистанционного обучения.Также материал может быть использован учениками, желающими углубить знания по теме, длясамостоятельного рассмотрения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4895 |
| Номер материала | 196 |