
Урок "Разложение на множители разности квадратов"

Краткое описание документа:
Как известно, любые формулы математики при желании могут быть инверсированы, то есть, обращены. В любом реальном равенстве, элементы которого имеют алгебраический смысл, можно обменять правую и левую части местами, не нарушив смысла всей формулы. Это аксиоматическое заключение делает многие практические равенства универсальными.
В предыдущих видео мы рассмотрели применение некоторых формул сокращенного умножения. Они часто используются в упражнениях со сложными многочленами или подобными равенствами.
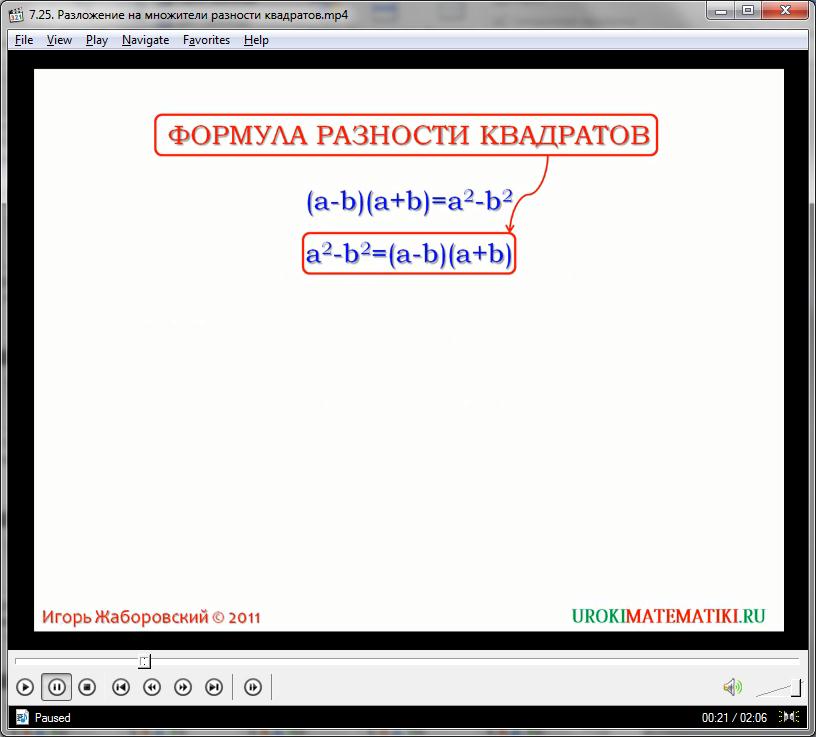
Например, одна из формул СУ гласит: произведение суммы и разности двух натуральных чисел равно разности квадратов этих чисел:
(а + с)(а – с) = а2 – с2
Это выражение алгебраически состоит из произведения многочленов в левой части, и из разности одночленов в правой. Обратим равенство:
а2 – с2 = (а + с)(а – с)
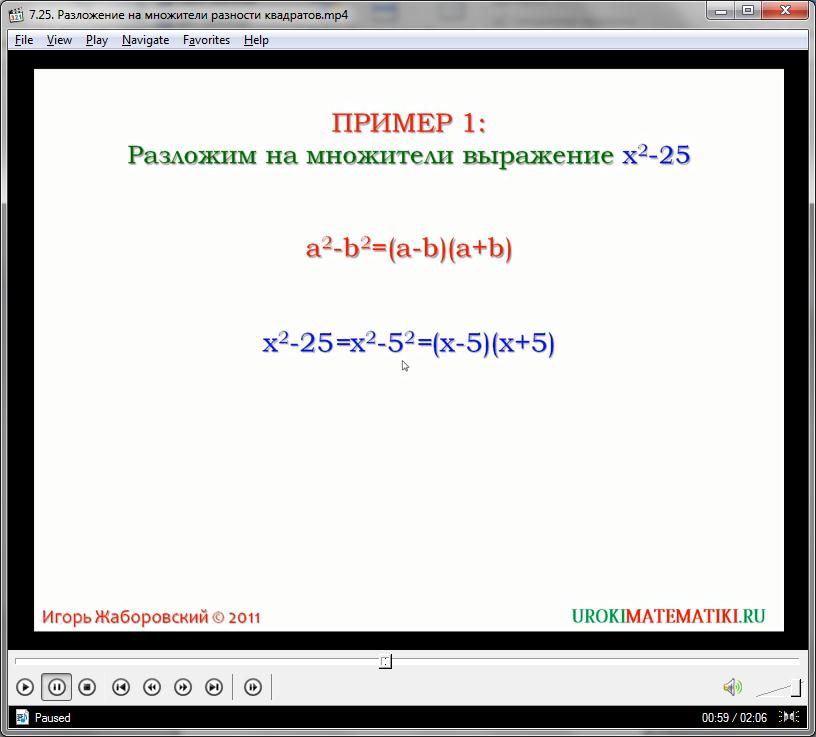
На словах новую формулу можно передать так: разность квадратов двух натуральных чисел равна произведению их суммы и разности. Данное тождество носит название «формула разности квадратов», и часто используется в линейной алгебре для преобразования разности натуральных квадратов в произведение. Рассмотрим следующий пример. Преобразуем выражение:
х2 – 25
х2 – 25 = (х + 5)(х – 5)
На первый взгляд, преобразованное выражение лишь удлинилось. Однако не стоит забывать, что порой приходится жертвовать уровнем сложности выражения для того, чтобы суметь правильно его сократить либо же с другой целью, диктуемой смежными темами математики. Например, необходимо найти значение выражения:
(2х2 – 18 – (х + 3)(х – 3)) / (х + 3)
Для того чтобы решить данное упражнение, произведем локальную группировку и вынесем за скобки двойку, обособив первые два элемента выражения:
(2х2 – 18 – (х + 3)(х – 3)) / (х + 3) = (2(х2 – 9) – (х + 3)(х – 3)) / (х + 3)
После этого необходимо применить обратную формулу СУ, чтобы преобразовать выражение таким образом:
(2(х2 – 9) – (х + 3)(х – 3)) / (х + 3) = (2(х + 3)(х – 3) – (х + 3)(х – 3)) / (х + 3)
В новом выражении существуют две полностью идентичные группы, имеющие единую основу, но разный коэффициент-множитель. Можно записать, что:
2(х + 3)(х – 3) – (х + 3)(х – 3) = (х + 3)(х – 3)
Тогда наше выражение преобразуется и легко упростится благодаря правилам сокращения дробей:
(2(х + 3)(х – 3) – (х + 3)(х – 3)) / (х + 3) = (х + 3)(х – 3) / (х + 3) = х – 3
Как можно заметить из нашего видеоурока, первичное усложнение иногда бывает очень полезным – оно помогает представить все выражение с иного ракурса, что способствует применению альтернативных вариантов развязок, а также иных формул и правил. Усложненное выражение всегда более универсально – к нему можно применить большее количество математических приемов.
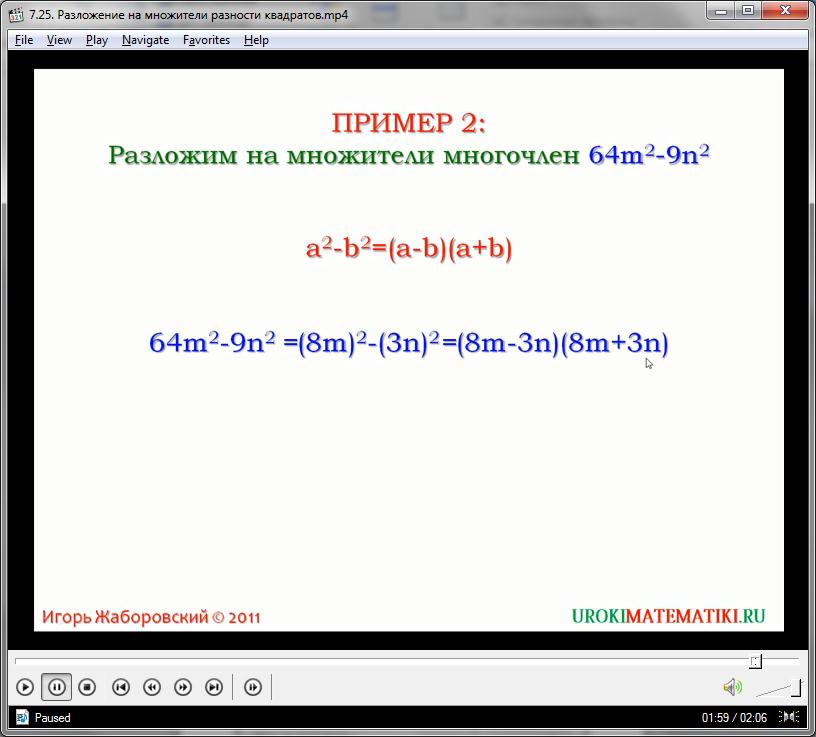
Рассмотрим ещё один пример удачного применения обратной формулы СУ. Упростим выражение вида 81а3 – 25а2:
81а4 – 25а2 = (9а2 + 5а)(9а2 – 5а)
Это выражение относительно легко решается, главное помнить о правилах переумножения одночленов с разными степенями и с одной переменной в качестве основы.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7430 |
| Номер материала | 467 |