
Урок "Разложение на множители с помощью формул квадрата суммы и квадрата разности"

Краткое описание документа:
При решении различных задач довольно часто надо умножить двучлены (а+b) на (а+b), или (а-b) на (а-b). Чтобы можно было сразу в таких случаях написать ответ, нужно знать тождества, которые называют формулами сокращенного умножения. Их знали и могли доказать еще древние китайские и греческие ученые-математики за много веков до начала нашей эры. Записывали их тогда не при помощи букв, а словами и доказывали геометрически (рассматривались только положительные числа). И формула, которую мы знаем как квадрат двучлена является простейшим случаем бинома Ньютона.
В формуле квадрата суммы «квадрат любого двучлена равен первому его члену в квадрате прибавить удвоенное произведение первого на второй члены и прибавить второй член в квадрате», а записать это можно так: (а+b) в квадрате равняется а квадрат плюс 2аb плюс b квадрат. И в формуле квадрата разности «квадрат двучлена равен квадрату первого его члена вычесть удвоенное произведение первого на второй члены и прибавить квадрат второго члена», а записать это можно так: (а-b) в квадрате равняется а квадрат минус 2 аb плюс b квадрат.
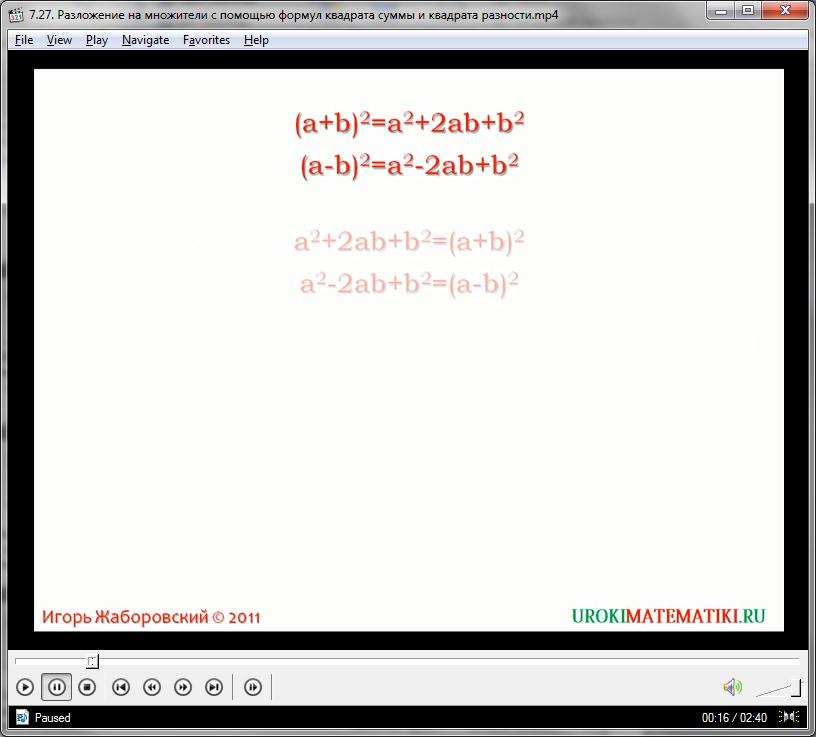
Если возьмем эти два тождества: формулы квадрата суммы (а+b) в квадрате и квадрата разности (а-b) в квадрате и в каждой из них поменяем местами левую и правую части, то получим новые формулы. В них указано, как трехчлены а квадрат плюс 2 аb плюс b квадрат и а квадрат минус 2 аb плюс b квадрат представить в виде квадратов двучленов, а именно, разложить на два одинаковых множителя. В этом видео мы и покажем, как правильно применить получение формулы на практике, ведь можно знание формул квадрата суммы и квадрата разности использовать в разложении на множители многочленов.
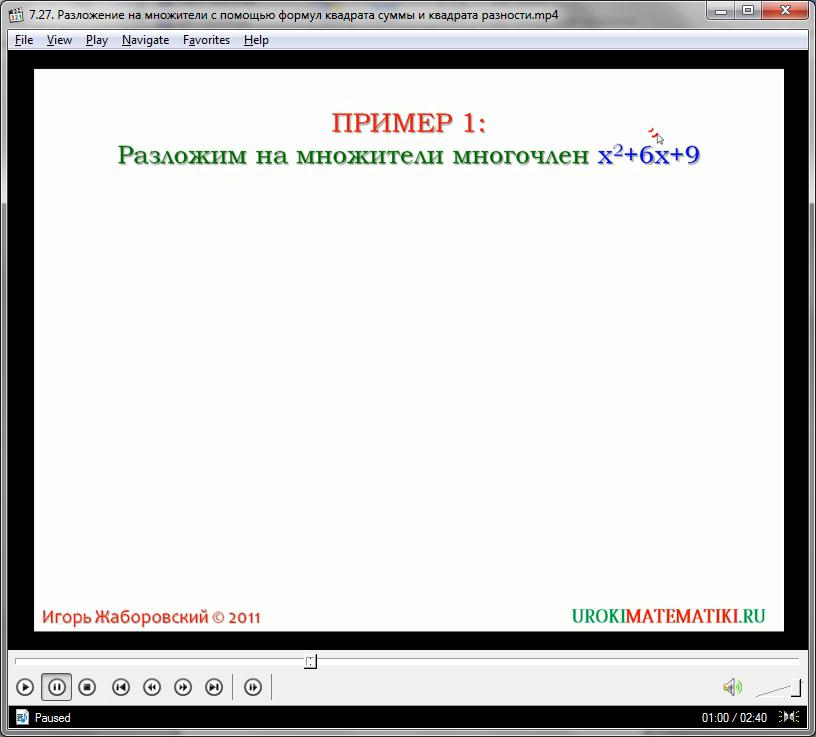
Рассмотрим в примере 1, как разложить на множители многочлен Х квадрат плюс 6Х плюс 9, используя формулу квадрата суммы. Его первое слагаемое Х квадрат является квадратом Х, а третье слагаемое 9 это квадрат числа 3. Второе слагаемое это удвоенное произведение Х и 3. То есть, 6Х – это то же самое, что 2 умножить на Х и умножить на 3. Поэтому Х квадрат плюс 6Х плюс 9 равен Х квадрат плюс 2 умноженное на Х и умноженное на 3 плюс 3 в квадрате. Но и по формуле это равно (Х+3) в квадрате.
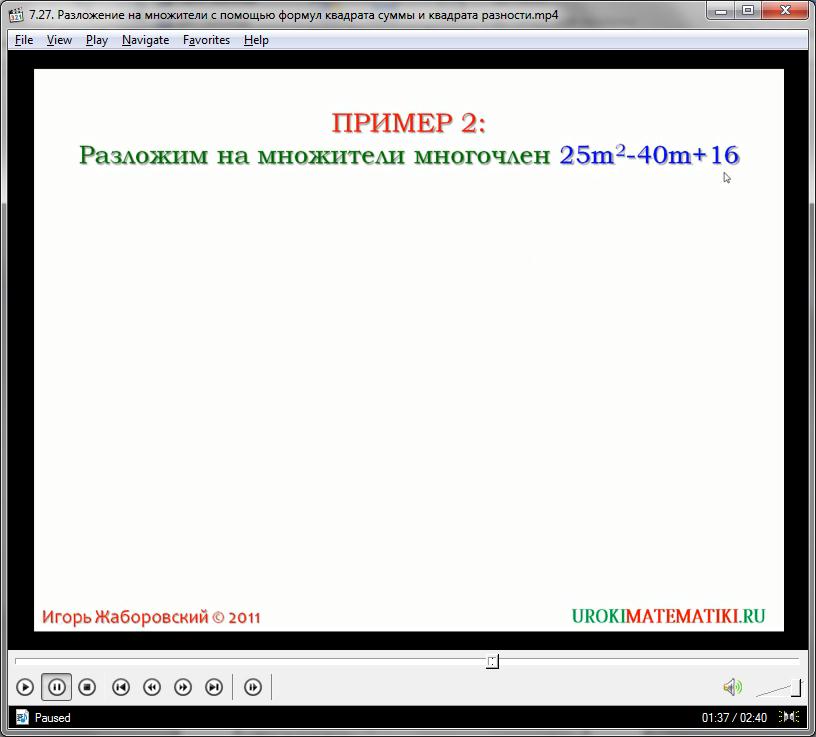
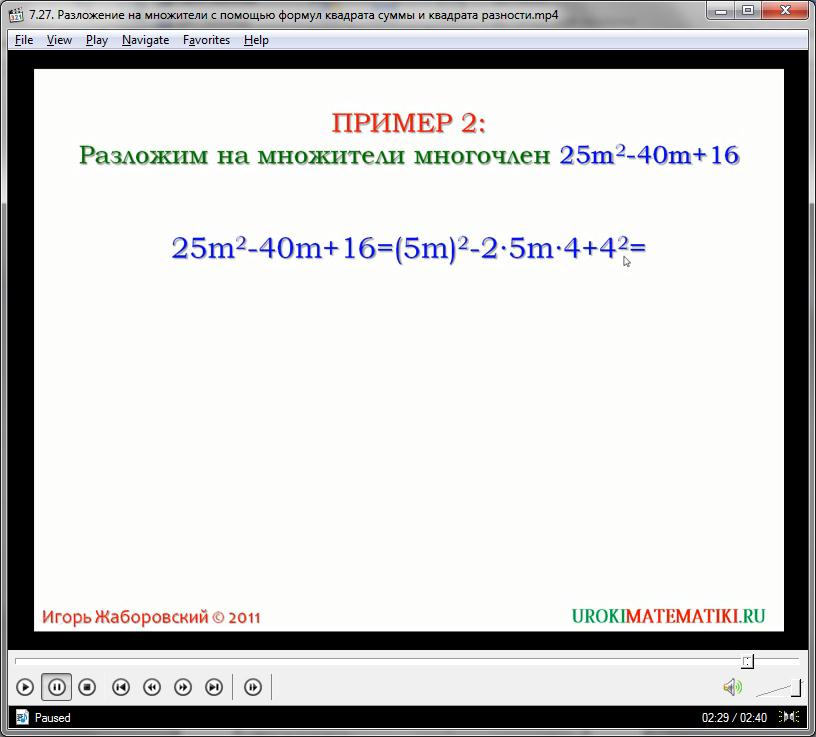
В примере 2 разложим на множители многочлен 25m квадрат минус 40mплюс 16, используя формулу квадрата разности. Первое слагаемое 25mквадрат представляет собой квадрат выражения 5m, а именно, 5mв квадрате, это 25m. Третье слагаемое 16 это квадрат числа 4, т.е. 4 в квадрате это 16. А второе слагаемое минус 40m– это удвоенное произведение чисел 5mи 4 со знаком минус, то есть, минус 40m– это тоже самое, что минус 2 умноженное на 5mи умноженное на 4. Следовательно, 25mквадрат минус 40mплюс 16 равно 5mв квадрате минус 2 умноженное на 5mи умноженное на 4 прибавить 4 во второй степени. И по формуле это равно (5m-4) в квадрате.
Раскладывать можно не только многочлены на множители, но и некоторые другие целые выражения которые можно представить в виде произведений многочленов. Иногда, чтобы многочлен разложить на множители, приходится применять не только эти, но и другие тождества, а так же одновременно пользоваться несколькими способами разложения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 14757 |
| Номер материала | 469 |