
Урок "Возведение в квадрат суммы и разности"

Краткое описание документа:
В представленном видео будем говорить о том, как возвести в квадрат сумму и разность двух выражений. Сначала определим правило возведения во вторую степень выражение aплюс b. Представим квадрат этой суммы как произведение двух одинаковых множителей: (a+b)2=(a+b)×(a+b). Теперь найдем произведение согласно правилу умножения двучлена на двучлен, то есть умножим сумму а и b на сумму а и b. В результате наше выражение примет вид: (a+b)2=(a+b)×(a+b)=a×a+a×b+b×a+b×b=a2+ab+ab+b2.Приведемподобныеслагаемые, а именно +abи +ab.Получим(a+b)2=(a+b)×(a+b)=a2+ab+ab+b2= a2+2ab+b2.
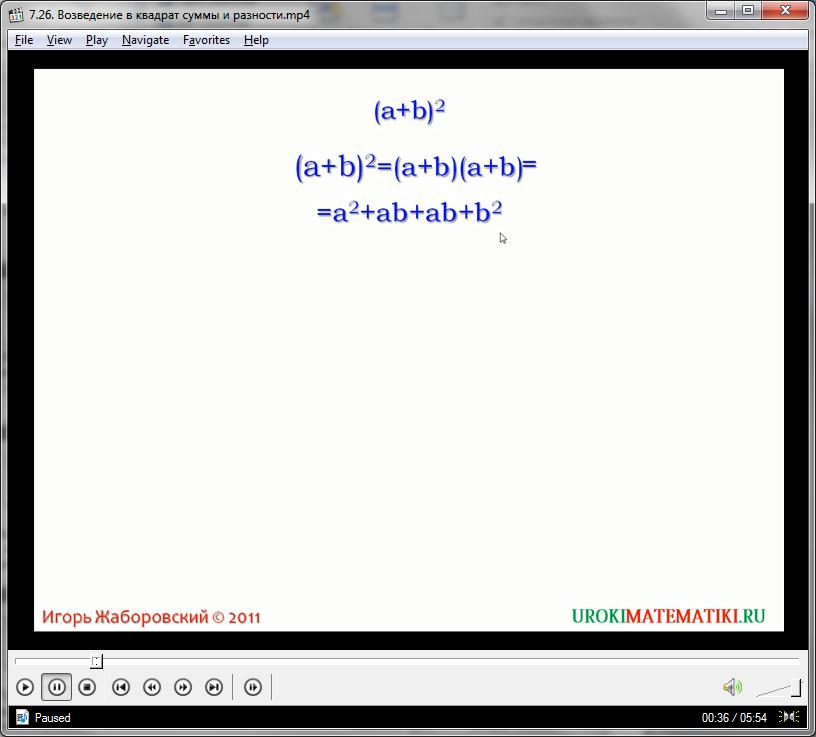
Итак, в конечном итоге, мы получили новое тождество: (a+b)2= a2+2ab+b2. Это будет еще одной из формул, упрощающих умножения. Ее называют «формула квадрата суммы выражений». По-другому, сумма двух выражений во второй степени равна первому выражению в квадрате, прибавить произведение первого выражения на второе, умноженное на два, и прибавить выражение два в степени 2.
Далее автор предлагает перейти к рассмотрению как использовать эти формулы. Пример первый. Запишем 5x+3 во второй степени в виде многочлена. Если применить тождество квадрата суммы (a+b)2= a2+2ab+b2, получаем (5+3x)2=(5)2+2×5×3x+(3x)2=25+30x+9x2.
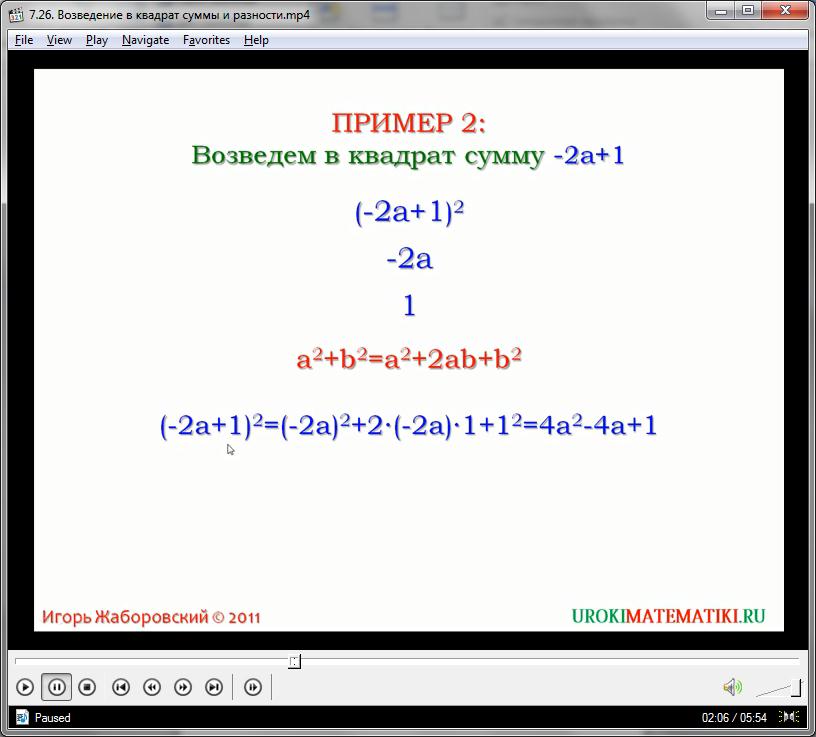
Второй пример. Необходимо минус 2а плюс 1 возвести в степень. (-2а+1)2 будет квадратом -2а прибавить 1. Применяем известную нам формулу квадрата суммы выражений (a+b)2= a2+2ab+b2. Имеем: (-2а+1)2=(-2а)2+2×(-2а)×1+12=4а2-4а+1.
Возведём aминус bв нужную степень. Представляем умножением двух одинаковых множителей (a-b)2=(a-b)×(a-b) квадрат этой разности. Умножая, врезультатеимеем (a-b)2=(a-b)×(a-b)=a×a+a×(-b)-b×a+(-b)×(-b)=a2-ab-ab+b2. Приведём подобные слагаемые: (a-b)2= a2-2ab +b2. В итоге, это становится формулой сокращённого умножения и носит название «формула квадрата разности 2 выражений». То есть, одно выражение минус второе в степени 2 будет равняться первому выражению во второй степени, отнять произведение двух выражений умноженное на два, прибавить второе выражение во второй степени.
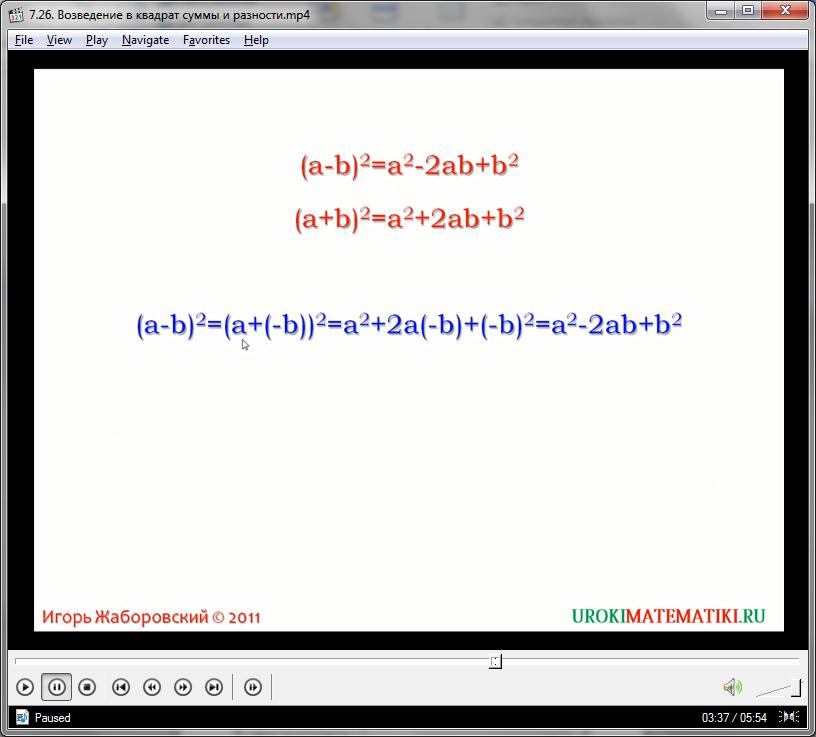
Формулу квадрата разности выражений можно легко получить из формулы квадрата суммы. Просто достаточно представить a-b через a+(-b). Получим (a-b)2=(a+(-b))2=a2+2×a×(-b)+(-b)2=a2-2ab+b2.
Пример три. Возведем в рассматриваемую степень 2 разность 4m-3. Применяем формулу разности квадрата (a-b)2= a2-2ab +b2 к степени 4m-3 в квадрате и имеем (4m-3)2= (4m)2-2×4m×3+32=16m2-24m+9.
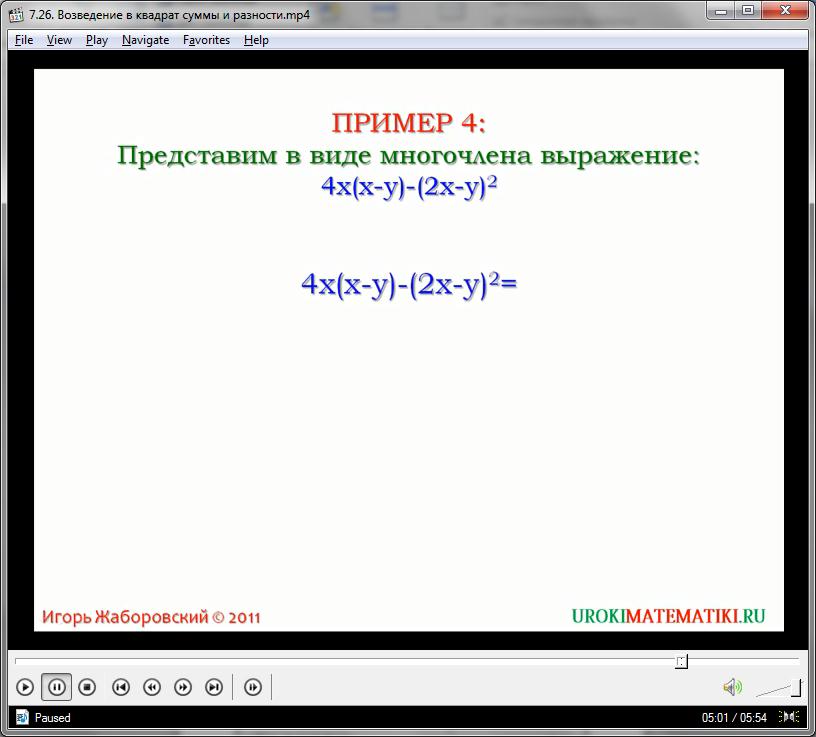
Пример четыре. Представим в качестве многочлена: 4x(x-y)-(2x-y)2. Выполним указанные действия. Получим 4x(x-y)-(2x-y)2=4x2-4xy-(4x2-2×2x×y+y2)=4x2-4xy-(4x2-4xy+y2). Далеераскроем скобки. 4x(x-y)-(2x-y)2=4x2-4xy-(4x2-4xy+y2)= 4x2-4xy-4x2+4xy-y2. Приводим подобные слагаемые и получим 4x(x-y)-(2x-y)2=4x2-4xy-4x2+4xy-y2=-y2, так как слагаемые 4x2 и -4x2, а также -4xy и +4xy взаимно уничтожились.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9260 |
| Номер материала | 468 |