
Урок "Умножение разности двух выражений на их сумму"

Краткое описание документа:
Решая различные примеры с многочленами, в которых приходится производить операции разложения полинома на множители, можно заметить, что некоторые выражения встречаются довольно часто. Числовые коэффициенты сугубо индивидуальны, а вот форма буквенного выражения имеет принципиально меньшую гибкость, поэтому многие уравнения имеют, на первый взгляд, общую основу.
В предыдущих видеолекциях мы ознакомились с преобразованием многочлена, которое производится, в основном, двумя путями. При вынесении общего множителя за скобки получается произведение одночлена (служащего основанием для всех членов начального полинома) на многочлен (представляющий собой алгебраическую сумму частных). А при способе группировки, многочлен разбивается на множители при использовании нескольких оснований (чаще всего, двух).
Некоторые стандартные формулы многочленов, наиболее часто используемые в линейной алгебре, рекомендуемы к запоминанию. Они имеют название «формулы сокращенного умножения», так как позволяют заметно сократить процесс решения многочлена. Например, рассмотрим выражение вида:
(а – с)(а + с)
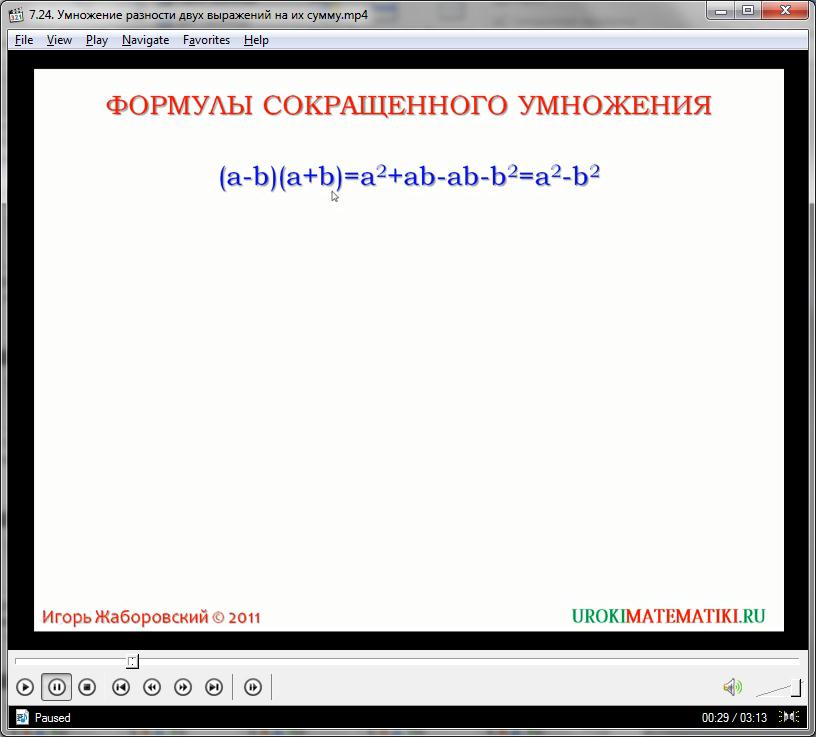
Оно достаточно простое, и его можно легко сформулировать словами: произведение суммы и разности двух произвольных переменных. Подобная конструкция неоднократно встречается как в простейших выражениях, которые нужно определить, так и в сложных уравнениях. Поэтому полезно выучить значение этого буквенного выражения. Вычислим его, пользуясь правилом перекрестного умножения:
(а – с)(а + с) = а2 + ас – ас – с2 = а2 – с2
Как видим, в процессе расчетов произведение переменных ас взаимосокращается, оставляя лишь квадраты. Можно сформулировать данную формулу следующими словами: произведение суммы и разности двух чисел равно разности квадратов этих чисел, или:
(а – с)(а + с) = а2 – с2
Применение данной формулы позволяет сократить количество действий, необходимых для сложных комплексных упражнений. Кроме того, очень часто ФСУ помогают преобразовать выражения так, что только после этой операции возможно получение ответа.
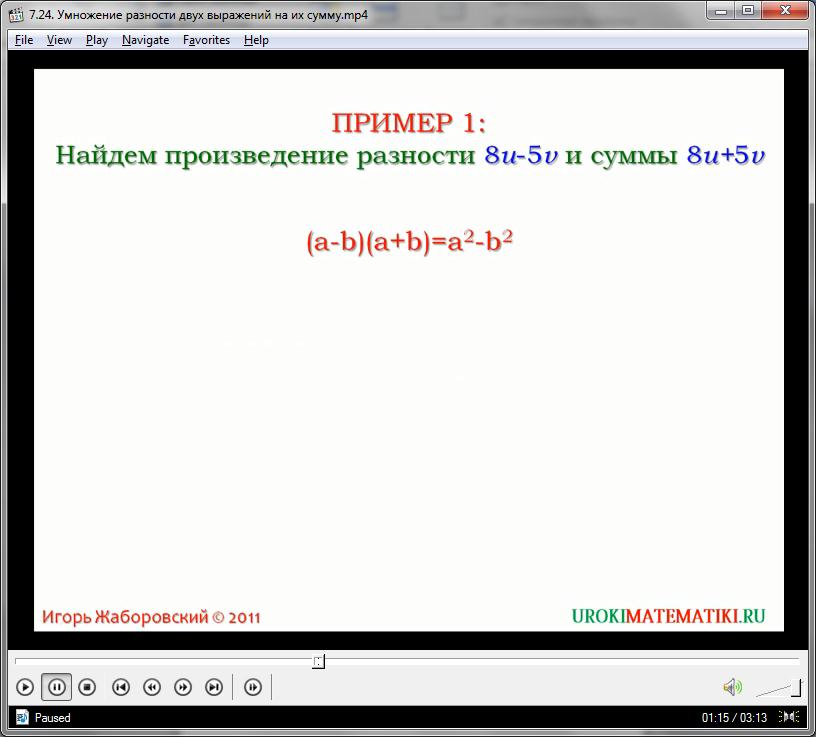
Приведем пример с видеоурока. Найти значение выражения:
(4а + 2с)(4а – 2с)
Решаем, используя ФСУ:
(4а + 2с)(4а – 2с) = (4а)2 – (2с)2 = 16а2 – 4с2
При решении этого упражнения необходимо помнить, что в квадрат, согласно формуле, возводится одночлен полностью, а не только буквенная часть. Если переменная стоит в некой степени, то она умножается на себя саму. Если при переменной коэффициент – то его так же нужно возводить в квадрат.
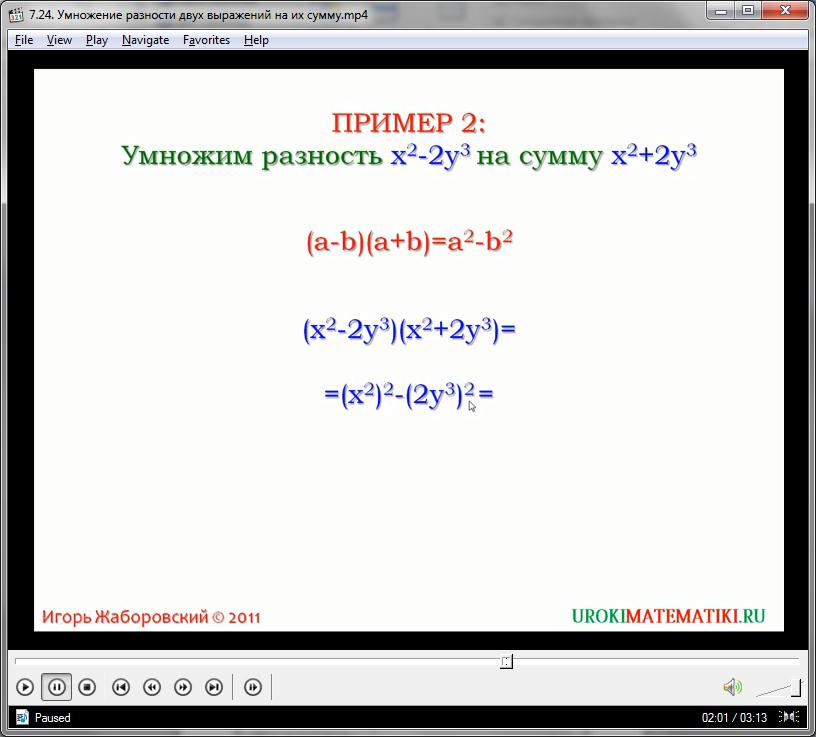
Рассмотрим более сложный вариант. Решим выражение, используя ФСУ:
(3а3 + 2с5)(3а3 – 2с5) = (3а3)2 – (2с5)2 = 9а6 – 4с10
Во многих других упражнениях приходится решать обратную задачу – приводить выражение к виду (а2 – с2) и разбивать его, согласно формулам сокращенного умножения, на произведение суммы и разности. Это бывает необходимым в тех случаях, когда многочлен нужно представить в виде произведения. Например, решим такую задачу. Представим в виде произведения следующее выражение:
2х2 – 5у2 + 7х2 + у2
Проведем алгебраическое сложение, а также используем ФСУ для быстрого преобразования:
2х2 – 5у2 + 7х2 + у2 = 9х2 – 4у2 = (3х + 2у)(3х – 2у)
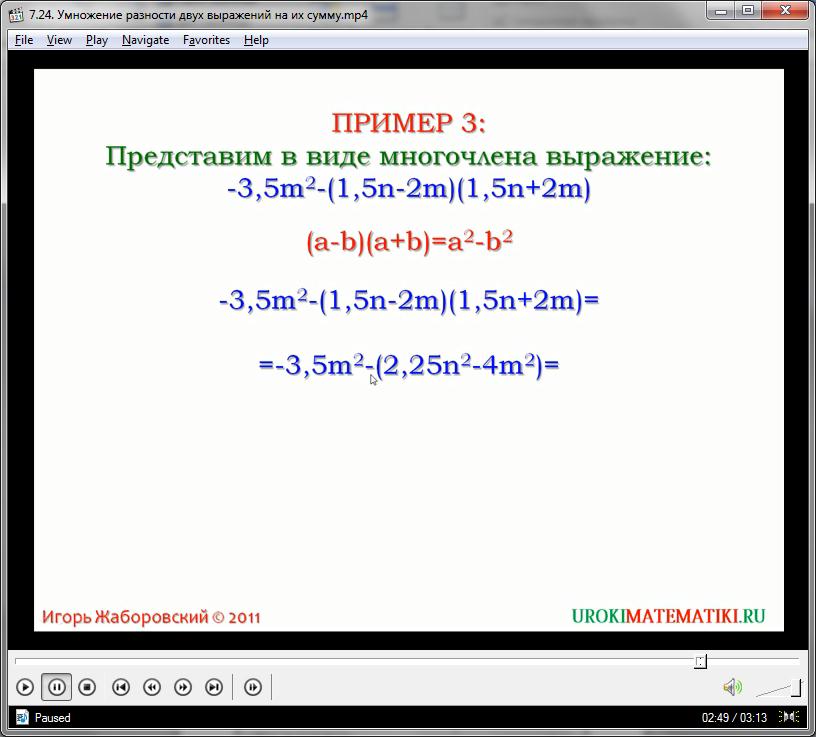
Формулы для быстрого произведения используются и в комплексе с другими элементами алгебры. Упростим выражение:
-3а(а – 1)(а +1) + (а + 9)(а – 9)
Несмотря на всю громоздкость, представляемое выражение легко разбивается при помощи двойного применения ФСУ. Получаем и решаем следующий многочлен:
-3а(а – 1)(а +1) + (а + 9)(а – 9) =
= -3а(а2 – 1) + а2 – 81 =
= -3а3 + а2 + 3а – 81
Таким образом, приемы сокращенного умножения позволяют заметно упростить решение многих математических задач.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7524 |
| Номер материала | 466 |