
Презентация "Возведение в квадрат суммы и разности"

Краткое описание документа:
Урок по теме «Возведение в квадрат суммы и разности» проводится в седьмом классе во время изучения формул сокращенного умножения. Тема является важной, ведь знания данного материала в дальнейшем часто используются. Поэтому целью любого урока будет стремление глубокого понимания и усвоения материала обучающимися.
Для наглядного объяснения материала практически на каждом уроке удобно использовать презентации. Данная презентация разработана в помощь учителю или обучающемуся. Но объяснение материала с использованием данной презентации должно выстраиваться по существующим уже знаниям у обучающихся.


слайды 1-2 (Тема презентации "Возведение в квадрат суммы и разности", пример)
Презентация, составленная автором, начинается с вывода формулы, которая и называется квадратом суммы. Вывод формулы основывается на преобразованиях, которые, в конечном счете, приводят к выражению. И это выражение нельзя уже больше изменить. Затем дается словесная формулировка полученной формулы, что развивает математическую речь обучающихся.


слайды 3-4 (примеры)
На этом ознакомление с материалом не заканчивается. Автор предлагает к полученной теории рассмотреть примеры. И на первом таком примере показано, как правильно следует применять только что изученную формулу. Но в математике бывают ситуации более сложные, с которыми у обучающихся постоянно возникают проблемы. Как например, со знаками. Для этого автор предлагает следующий пример, который иллюстрирует правильное применение формулы, не теряя при этом знаков.

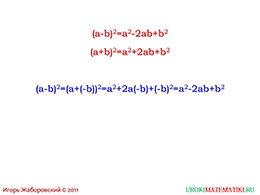
слайды 5-6 (формула квадрата разности двух выражений)
Так на уроке может быть рассмотрен квадрат суммы, но в теме был заявлен еще и квадрат разности. Поэтому далее в презентации вводится формула квадрата разности и дается словесная формулировка данной формулы. И затем все идет по аналогии с квадратом суммы.
Затем автор предлагает сравнить две полученные формулы, делая акцент на то, что равенства отличаются только лишь знаком между выражениями в левой части и знаком перед вторым членом многочлена из правой части.


слайды 7-8 (примеры)
После рассмотрения теоретической части, которая касается квадрата разности, автор предлагает продемонстрировать суть на примерах. И первый такой пример, как и в случае квадрата суммы, показывает, как правильно следует применять данную формулу. Но это лишь один из самых простых случаев, который может встретиться в курсе алгебры. Но очень часто перед обучающимися стоит задача решить более сложные задачи, поэтому автор предлагает следующий пример, где нужно сложное выражение представить в виде многочлена, то есть упростить данное выражение. Сначала требуется раскрыть скобки в первом случае и применить формулу квадрата разности во втором. Затем путем математических преобразований упростить полученное выражение, и когда с выражением уже ничего нельзя сделать, весь процесс завершается. Таким образом, полученное выражение и будет искомым.
Данная презентация может применяться на уроках в 7 классе. Если для учителя необходимо, он может дополнить ее на свое усмотрение. Ведь здесь включено только самое необходимое, чтобы взять ее как заготовку. Обучающимся данной презентации также будет достаточно, чтобы самостоятельно изучить материал по данной теме. Также материал будет полезен для внеклассных дополнительных занятий по математическим дисциплинам.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4079 |
| Номер материала | 209 |