
Презентация "Общие методы решения уравнений"

Краткое описание документа:
Презентация «Общие методы решения уравнений» - наглядное пособие для изучения данной темы на школьном уроке. После изучения множества видов уравнений можно выделить общие методы их решения. Каждый вид уравнений имеет особенности, которые необходимо учитывать при выборе способа решения. Задача учителя – выработать у учеников навыки выбора оптимального способа решения уравнения, владения всеми известными способами решения. Поэтому в данной теме рассматривается множество изученных способов решения уравнений, описываются примеры их применения.


Использование презентации с целью обеспечения наглядности учебного материала очень эффективно. Теоретические положения, требующие запоминания, выделяются цветом, рамками, другими способами, способствующими лучшему процессу запоминания. В презентации возможна вставка рисунков, выполнение наглядных построений, в которых используются анимационные эффекты, выделение цветом деталей, представляется детальное, удобное описание решений задач.

Презентация начинается небольшим отступлением в историю математики, словами Г.Лейбница о выборе метода решения математических задач. В них отмечается полезность метода, который помогает изначала предвидеть и затем, в процессе решения данным методом, подтвердить достижение цели. На слайде представлен портрет Лейбница, указаны даты его рождения и смерти. Далее дается определение методов решения уравнений. Указано, что это приемы, способы, помогающие решить уравнения. Определение выделено в рамке и предложено к запоминанию. Более общим понятием является понятие общего метода решения уравнений – способов и приемов, используемых для решения уравнений разного типа. Определение также выделено в рамке.


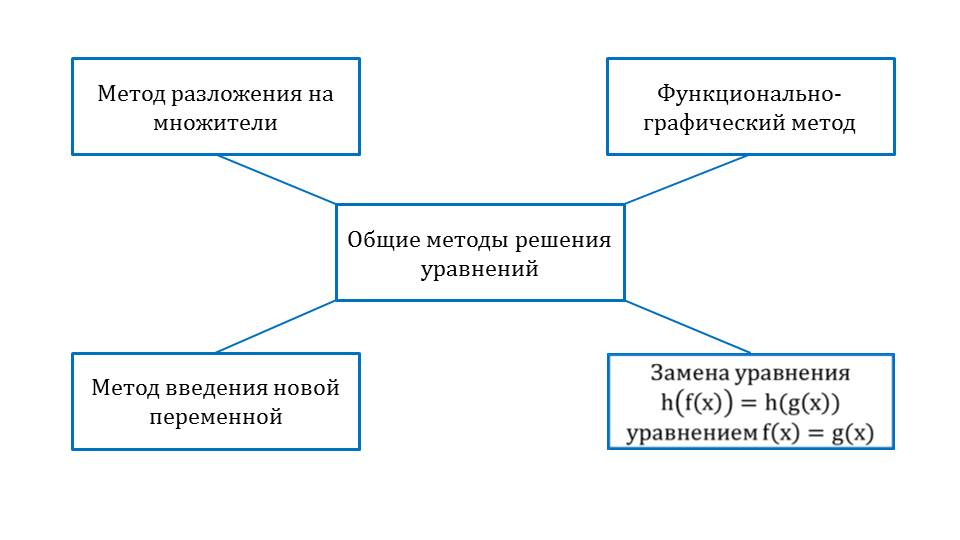
Далее схематично представлены виды общих методов решения уравнений. На схеме отмечены основные методы:
- разложения на множители;
- функционально-графический;
- введение новой переменной;
- замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x).


На слайде 5 отмечается, что последний способ решения уравнений справедлив только для монотонной функции, которая принимает каждое значение только один раз. Данное правило выделено цветом, чтобы отметить важность особенности его применения. На слайдах 6-8 рассматриваются примеры решения уравнений, в которых применяется указанный способ решения. В примере 1 описывается решение уравнения (3х-7)5=(2х+3)5. Для степенной функции, являющейся монотонной, рассмотренный выше способ замены уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x) применим, поэтому исходное уравнение приравнивается к уравнению 3х-7=2х+3. Решив это простое уравнение, получаем его корень х=10. Пример 2 рассматривает решение уравнения (8-2х)2=(х2+5)2. Руководствуясь правилом применения способа замены уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x), можно сделать вывод о том, что, так как данная функция не является монотонной, то и метод применить нельзя. В примере 3 решается уравнение log3(x+1)+ log3(x+3)=1. Сначала оценивается область допустимых значений решений уравнения. Так как под знаком логарифма по основанию 3 может быть только положительное число, то решаются неравенства х+1>0 и х+3>0, общее решение которых х>-1. Так как оба логарифма в сумме по одному основанию, преобразуем выражение log3(x+1)+ log3(x+3)= log3(x+1)(x+3). Логарифмом по этому же основанию представляем число 1= log33. После преобразования обеих частей уравнения к виду h(f(x))=h(g(x)), можем применить известное правило. Решение сводится к решению уравнения (х+1)(х+3)=3. Это квадратное уравнение, корнями которого являются х1=0 и х2=-4. Зная ограничение на значение решения, отмечаем, что решением исходного уравнения есть только х=0.


Метод замены уравнения отдельно рассматривается для показательного, логарифмического и иррационального уравнения на слайде 9. Чтобы применить метод для показательного уравнения, оно приводится к виду af(x)=ag(x), где положительное а, не равное 1. Для логарифмического уравнения это вид logaf(x)= logag(x), где также положительное, не равное 1, число а. Иррациональное уравнение для применения метода замены уравнения должно иметь вид n√f(x)=n√g(x). Примером такого разложения служит способ решения уравнения sinx+sin2x+sin3x=0. После преобразования суммы первых двух слагаемых в произведение 2sinx2xcosx и выведения общего множителя, получаем вид sin2x(2cosx+1)=0.
Решение исходного уравнения сводится к решению двух простых sin2x=0 и 2cosx+1=0. Из первого уравнения х=πn/2 для целых n. Из второго уравнения х=+-arccos(-1/2)+2πk для целых k. Из множества данных решений состоит общее решение исходного уравнения.


На слайде 10 изложена суть метода разложения на множители. Отмечается, что возможности преобразования уравнения в вид f(x)g(x)h(x)=0 его можно заменить совокупностью уравнений f(x)=0, g(x)=0, h(x)=0.
На слайде 12 рассматривается суть метода введения новой переменной. Отмечается, что для решения уравнения f(x)=0, имеющего вид р(g(x)), можно ввести новую переменную у= g(x), получая уравнение р(у)=0. Решая его, определяются корни у1, у2 и т.д. далее рассматриваются примеры применения метода для решения задач. В примере 5 требуется найти решения уравнения 4х-10·2х-1=24. Введя новую переменную t=2х, t>0 получаем уравнение t2-5 t-24=0. Решив его, находим t=8, то есть х=3. Пример 6 описывает решение уравнения log25x-log√5x-3=0. Вводится новая переменная t= log5x. Через нее выражаем исходное уравнение – оно приобретает вид t2-2 t-3=0. Решив уравнение, получаем значения t1=3, t2=-1. Подставив значения в формулу для определения корней, получаем х=125, х=0,2.


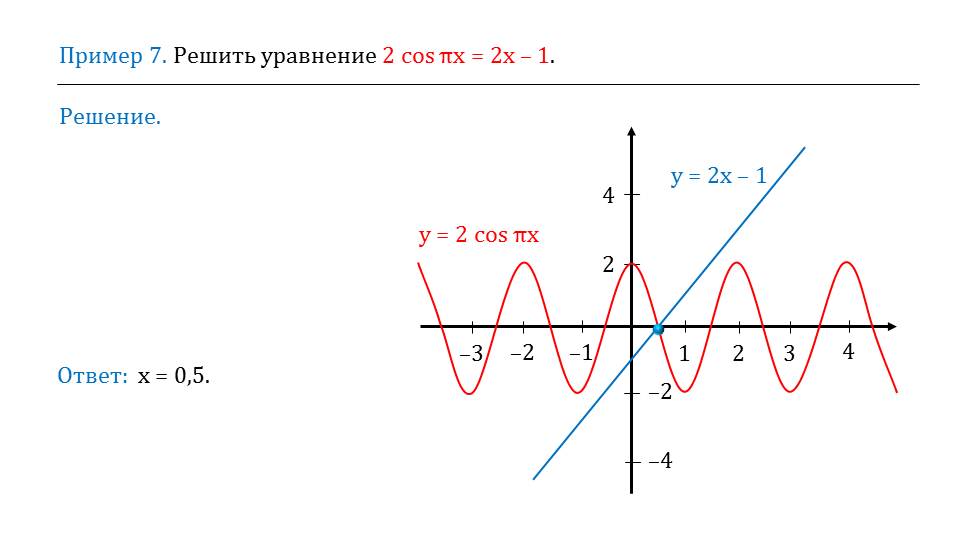
На слайде 15 изложена суть функционально-графического метода решения уравнения f(x)=g(x). Данный метод основан на определении абсциссы точки пересечения графиков функций у= f(x)и у=g(x). Примером применения метода служит пример 7, в котором необходимо решить уравнение 2cosπx=2x-1. На слайде демонстрируется решение данного уравнения функционально-графическим методом. На координатной плоскости строится синусоида, соответствующая функции у=2cosπx и прямая у=2x-1. Точкой пересечения данных графиков будет х=0,5 – это и есть решение уравнения.

На слайде 17 описываются свойства функций, которые важны для выбора метода решения уравнения – монотонность, ограниченность, четность, периодичность. Также отмечается особенность нахождения корней для функции f(x)=g(x), где одна из функций возрастает на промежутке, а вторая – убывает. Отмечается, что в этом случае может быть не более одного корня, который, к тому же, находится также методом подбора. При ограниченной сверху функции f(x) и ограниченной снизу функции g(x) так, что максимальное f(x) равно минимальному g(x), уравнение f(x)=g(x) будет равносильным системе уравнений f(x)=А и g(x)=А. В последнем примере описывается решение уравнения cos((x2-8x)/5)=x2+1. Очевидно, максимальным значением косинуса есть 1, а минимальным значением x2+1 также есть 1. Поэтому достаточно решить систему cos((x2-8x)/5)=1 и x2+1=1. Решение системы х=0. Задача решена.


Презентация «Общие методы решения уравнений» обеспечивает наглядность учебного материала на традиционном уроке математики. Также наглядное пособие может быть полезно учителю, выполняющему дистанционное обучение. Чтобы облегчить понимание и запоминание материала учениками, недостаточно хорошо усвоившими тему на уроке, презентация может быть рекомендована для самостоятельной работы дома.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 15013 |
| Номер материала | 1042 |