
Презентация "Однородные тригонометрические уравнения"

Краткое описание документа:
Презентация на тему «Однородные тригонометрические уравнения» является отличным обучающим материалом для школьников 10 класса. Она содержит слайды, которые передадут суть однородных тригонометрических уравнений, покажет, как их необходимо решать и какими свойствами они обладают?
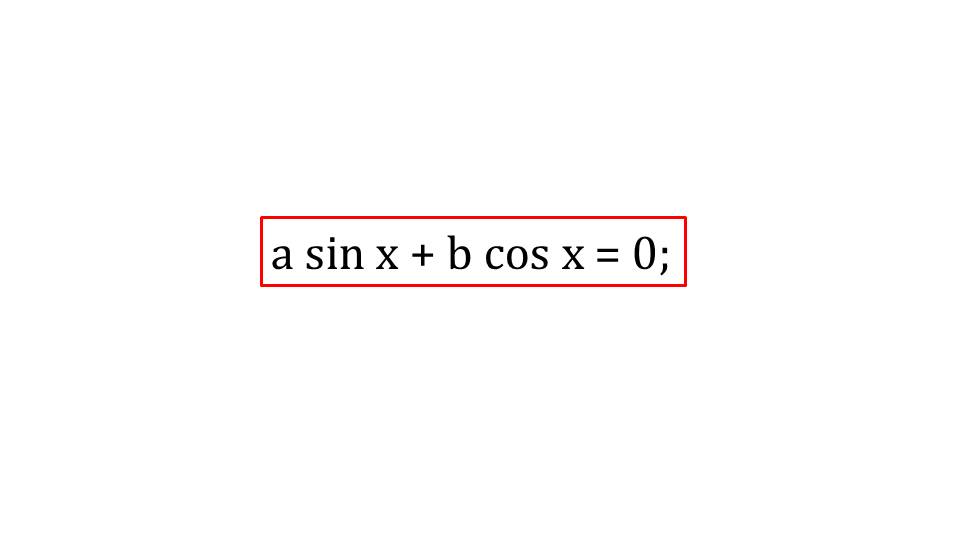

Материал подойдет для использования во время урока либо для индивидуальных занятий. Он является достаточно информативным и составлен грамотно специалистами. При изучении с использованием презентаций, восприятие темы во многом упроститься. Иллюстрации и понятные записи сделают процесс обучения более простым и интересным.

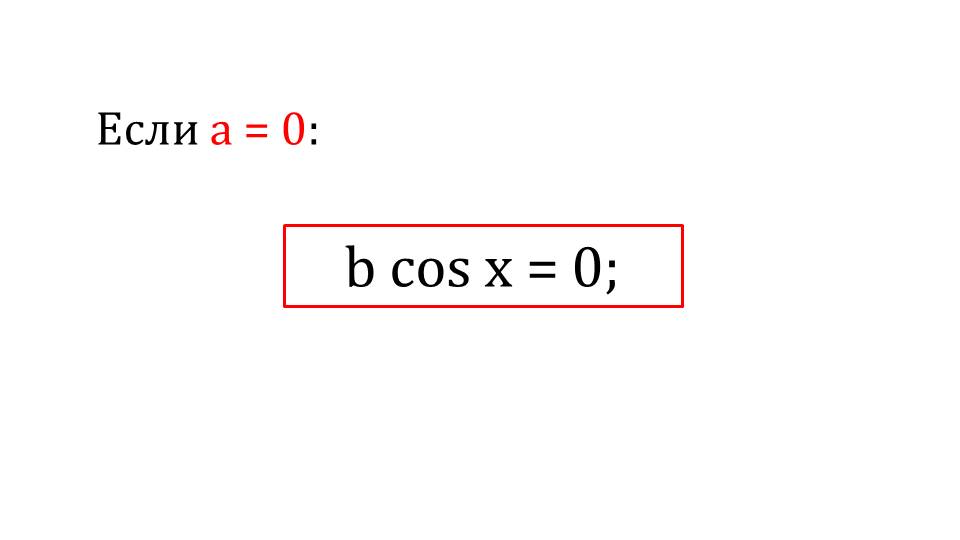
На первом слайде презентации предлагается школьникам посмотреть на общий вид однородных тригонометрический уравнений. Представляет оно собой сумму синуса с некоторым ненулевым коэффициентом с косинусом, аналогично, с некоторым иным ненулевым коэффициентом.
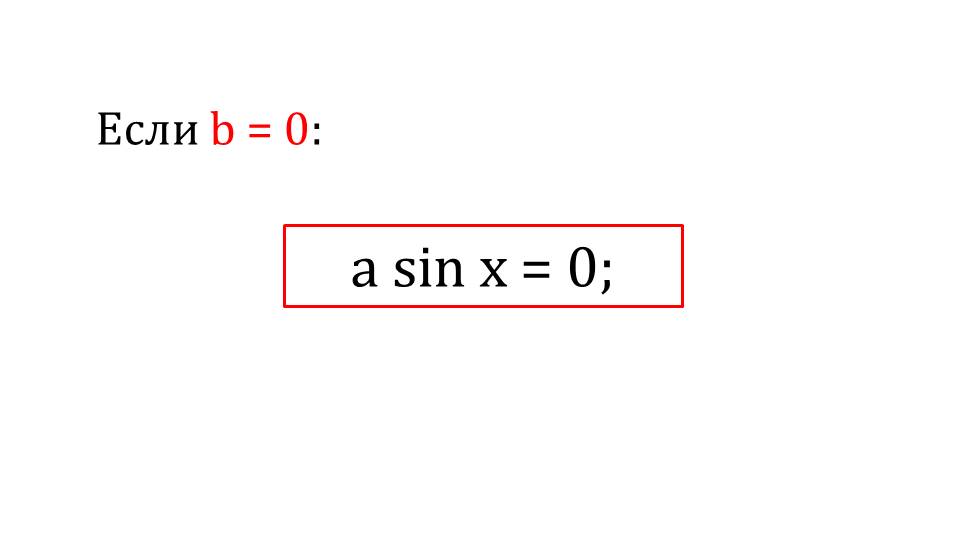

Данное уравнение является однородным первой степени. Далее приводится общий вид однородного тригонометрического уравнения второй степени.
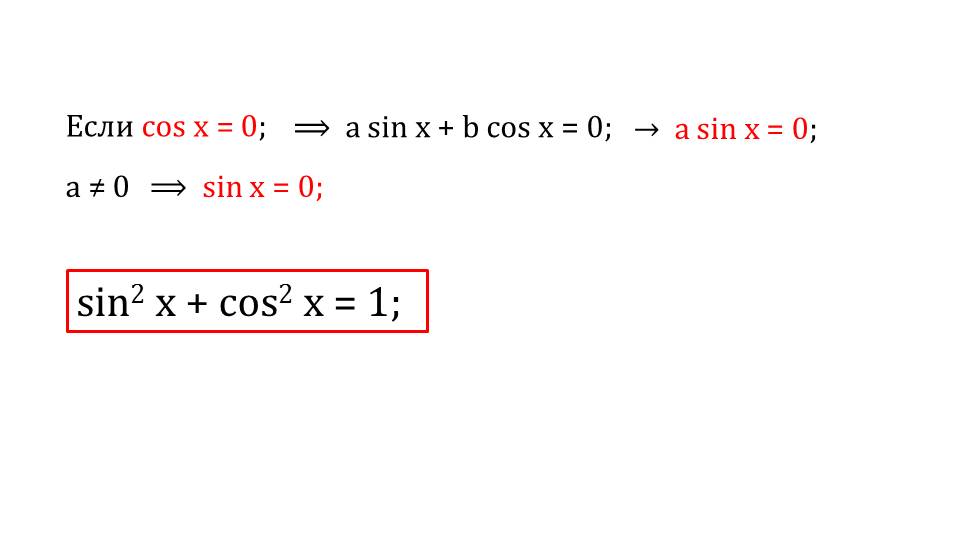
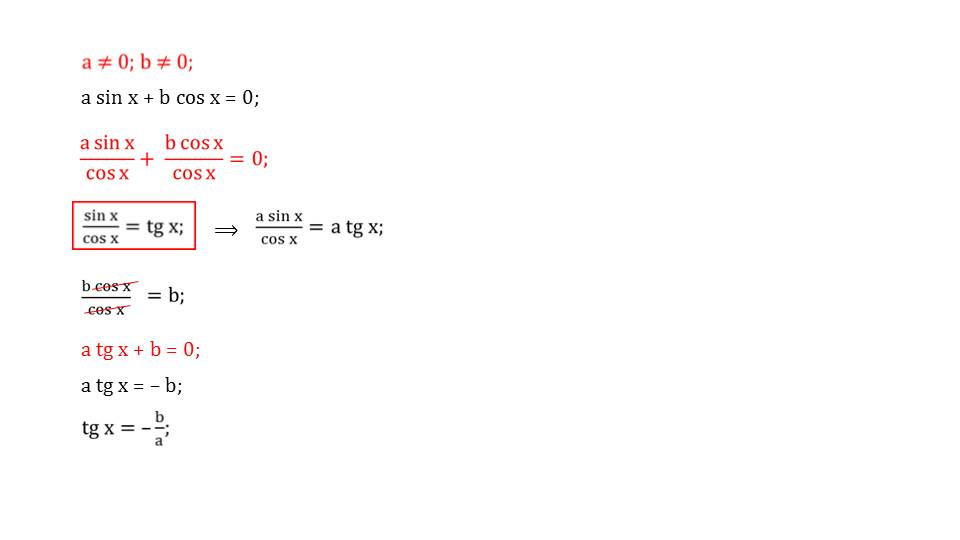
Что же произойдет, если один из коэффициентов в однородном тригонометрическом уравнении будет равен нулю? Получим обычное тригонометрическое уравнение, которое ранее было рассмотрено.


Отмечается, что коэффициенты одновременно не могу равняться нулю, иначе получим тавтологию 0=0.
Для того чтобы решить подобного рода уравнения, необходимо поделить оба слагаемых на cos.
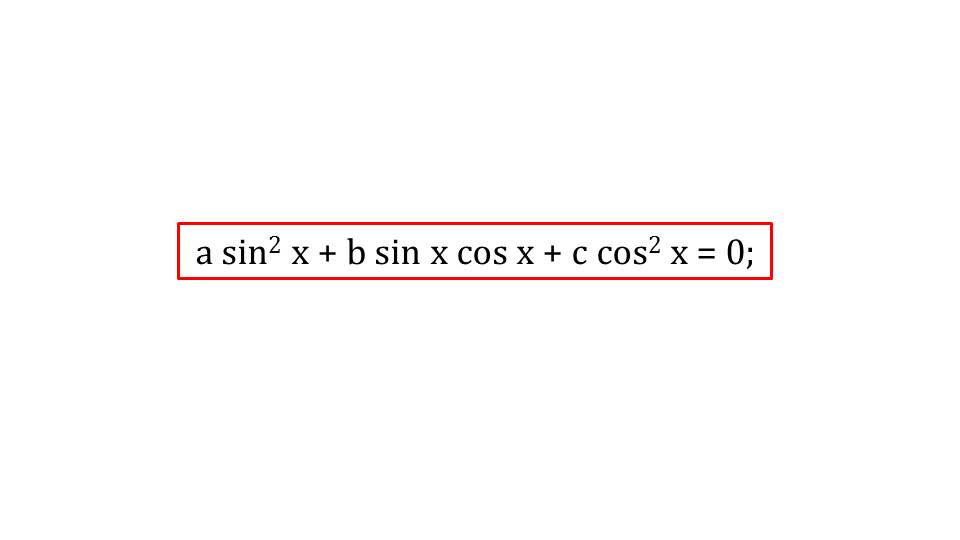

Почему именно такой метод? Ответ на этот вопрос содержится в предыдущих слайдах, где напоминается школьникам пройденные тригонометрические формулы.

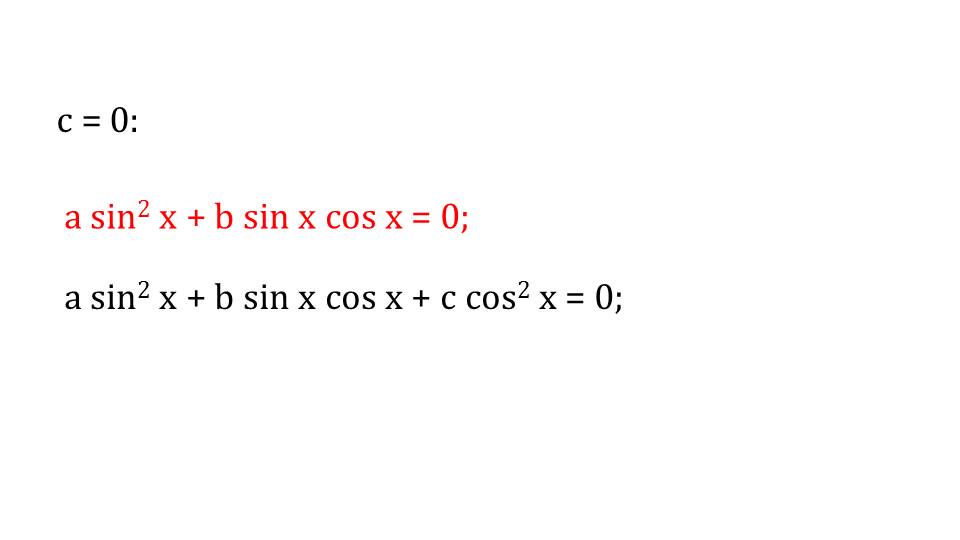
Приводится практический пример с подробным рассмотрением.
Далее аналогичным образом рассматривается решение однородных тригонометрических уравнений второй степени.


Приводится краткий и понятный алгоритм, с помощью которого можно легко справиться с подобными заданиями.
Закрепляется алгоритм практическим примером.


Презентация очень кратко и информативно донесет до школьников достаточно непростой материал. Примеры закрепят информацию на практике.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3749 |
| Номер материала | 810 |