
Презентация "Понятие корня n-й степени из действительного числа"

Краткое описание документа:
Презентация «Понятие корня n-й степени из действительного числа» используется как наглядный материал для объяснения нового материала по данной теме. В ходе демонстрации презентации учителю легче сформировать представление о корне n-й степени, его свойствах, научить применять теоретические сведения для решения математических задач. Демонстрируется много примеров, помогающих освоить графическое решение уравнений, выражение которого состоит из корня n-й степени, подробно разбирается решение задач.
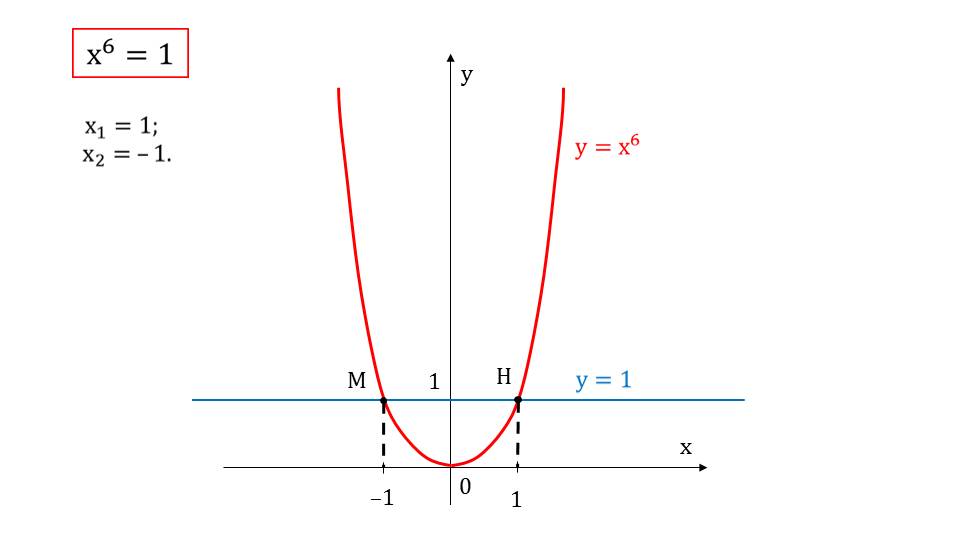
Демонстрация начитается с примеров решения уравнения графическим способом. На первом слайде представлено уравнение х6=1. На рисунке изображается парабола, которая представляет график функции х6=1. На рисунке график выделен красным цветом. Параболу пересекает прямая у=1, которая графически отображает правую часть уравнения. На рисунке отмечены точки пересечения М и Н двух графиков. Абсциссы этих точек и будут решением данного уравнения – х1=-1 и х2=1.
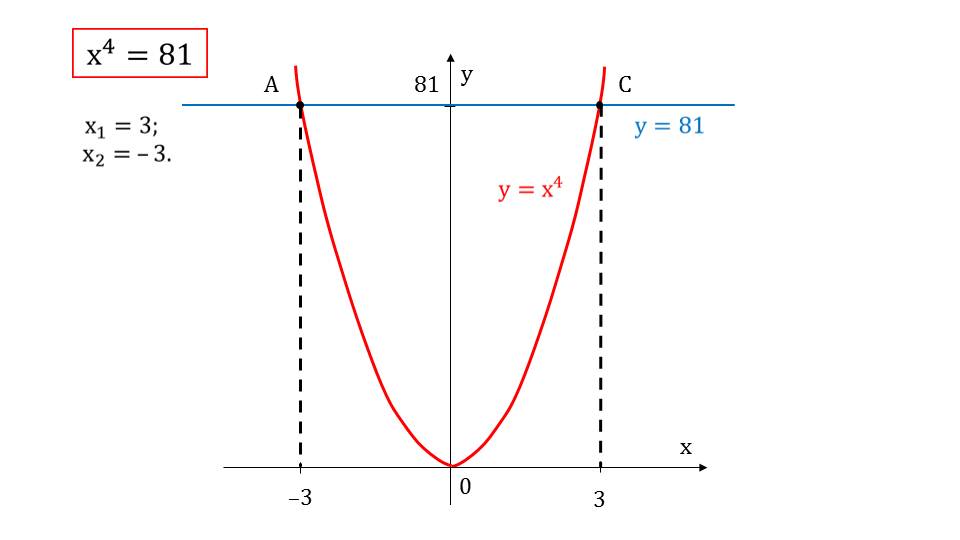
На втором слайде представлено графическое решение уравнения х4=81. На рисунке изображена парабола, соответствующая графику функции у= х4. Также изображена прямая, которая отражает функциональную зависимость у=81. Решение уравнения определяется в точках пересечения графиков у=81 и у= х4. На координатной плоскости отмечаем абсциссы точек пересечения А и С. Решениями данного уравнения являются х1=3 и х2=-3.


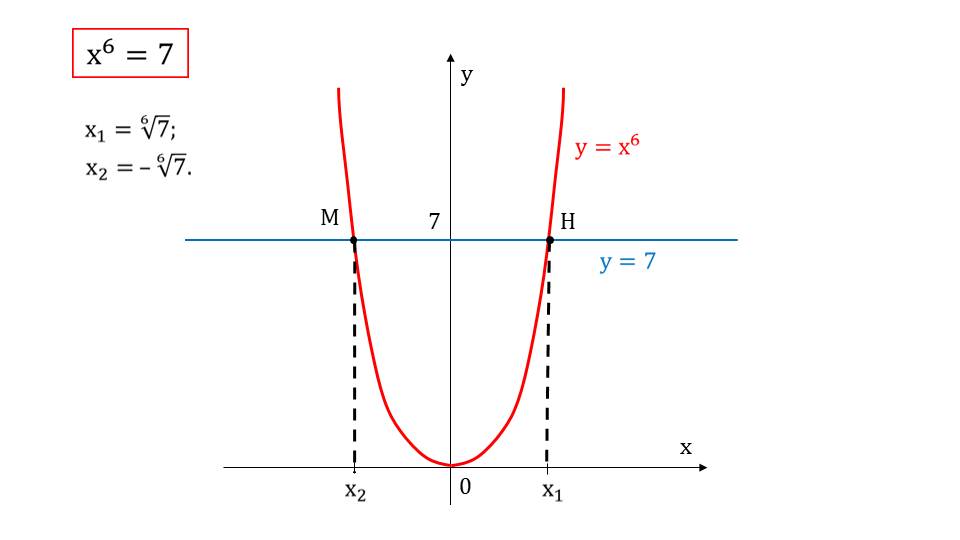
На слайде 3 представлено уравнение х6=7 и графическое его решение. Уравнение также разбивается на две части – левая часть отражает график решения уравнения у= х6, а правая часть уравнения представляется графиком функции у=7. Решение уравнения можно найти в точках пересечения графиков. Абсциссы этих точек х1=6√7 и х2=-6√7 являются решениями уравнения. Данные точки отмечены на оси абсцисс.


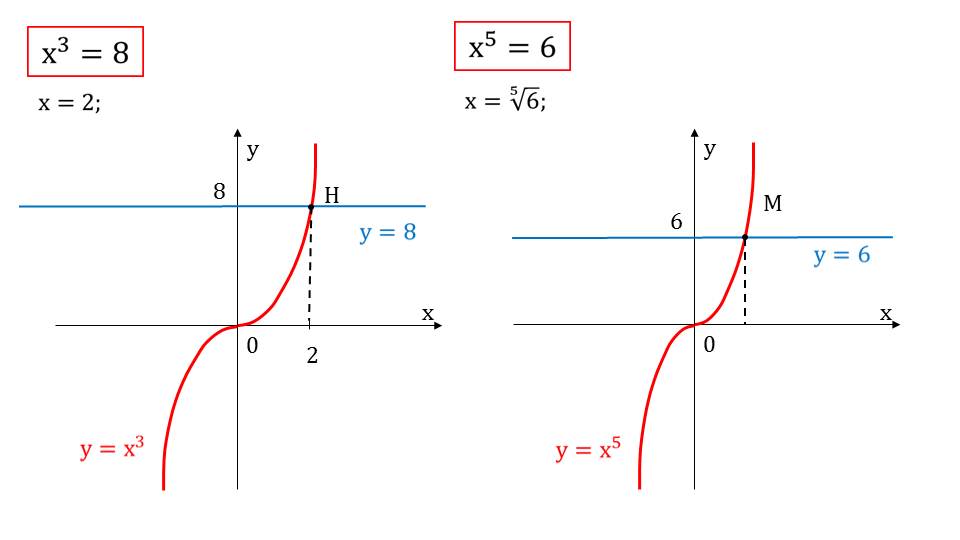
Слайд 4 представляет решение двух уравнений х3=8 и х5=6. Аналогично предыдущим примерам, к каждому уравнению на координатной плоскости изображается график функции, представляющей левую часть уравнения и правую часть. Графики уравнений у= х3 и у= х5 - кубические параболы. В первом уравнении находим решение уравнения в точке пересечения графика функции у= х3 и прямой у=8. Корнем уравнения является х=2, абсцисса точки пересечения. Также решением второго уравнения является абсцисса точки пересечения прямой у=6 и у= х5 – х=5√6.


Вывод из рассмотренных уравнений записывается на слайде 5 в виде правила, которое определяет, что решениями уравнений хn=a, в которых n – четное натуральное число и положительное а, являются корни х1=n√a и х2=-n√a. Правило рекомендуется к запоминанию. Отдельно рассматривается решение уравнения хn=0. Отмечается, что его единственный корень х=0.
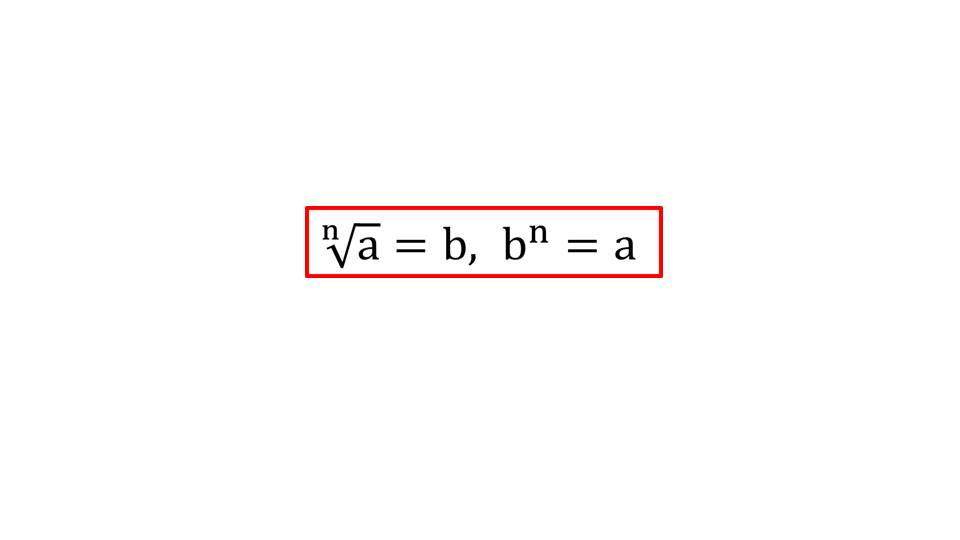
Далее обобщается понятие корня n-й степени, взятого из неотрицательного числа, где n – натуральное число, большее 1. Определяется, что таким корнем есть неотрицательное число, которое после возведения в степень n дает число а. Для запоминания выводится на экран обозначения корня n-й степени n√a, заключенное в рамку для запоминания.
Рассматриваются свойства корня n-й степени. На слайде 10 отмечается, что для неотрицательного а и натурального n, большего 1, справедливо, что значение корня n√a также неотрицательно, а при возведении корня в степень (n√a)n=a. Если b – значение корня n√а, то при возведении в степень bn получаем число а.


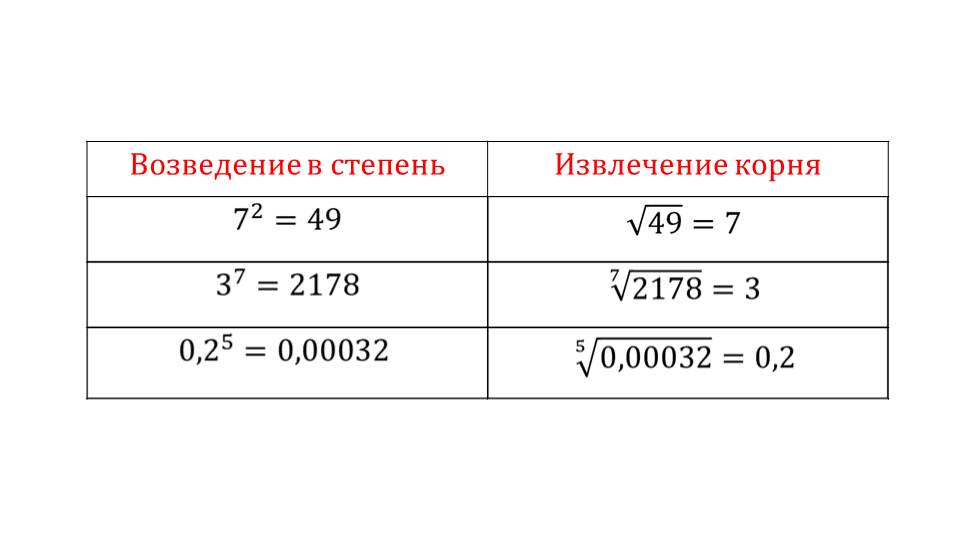
Для усвоения изученного материала на слайде 12 приводятся примеры нахождения значения корня некоторой степени из числа и связи с возведением этого числа степень корня. В таблице найдены значения √49=7, а рядом отмечено, что 72=49. Аналогично раскрыта связь 7√2178=3 и 37=2178, 5√0,00032=0,2 и 0,25=0,00032.
Далее рассматриваются примеры решения примеров с использованием изученного материала. На слайде 13 описывается решение задания, в котором требуется вычислить 6√64, 3√0,216, 5√(32/729), 4√55. На основании изученных свойств корня n-й степени из числа, определяем, что 6√64=2, 3√0,216=0,6, 5√(32/729)=2/3, 4√55≈2,64. Решение проверяется возведением полученного значения в степень корня. Для нахождения решения последнего примера подстановкой определяется более близкое значение к искомому.


На следующем слайде подобное правило определяется для хn=a, где n – нечетное натуральное число и положительное а. Отмечается, что в этом случае уравнение имеет один корень, который равен х=n√a. Правило также заключено в рамку и рекомендовано для запоминания.
На слайде 14 представлено определение корня степени n (нечетной) из отрицательного а. Отмечено, что это неотрицательное число m, дающее при возведении в n значение а. Определение выделено в рамку и рекомендовано к запоминанию.


Отдельно на слайде 15 рассматривается случай, когда подкоренное выражение является отрицательным числом, при этом степень корня – нечетная. Отмечается, что в этом случае результат вычисления корня будет отрицательным числом, а возведя в степень n корень n-й степени, получаем подкоренное выражение.
Далее рассматривается решение примера 2, в котором нужно найти решение уравнения 5√(3-5х)=3. Чтобы решить уравнение, обе его части возводятся в пятую степень (5√(3-5х)) 5=35. Таким образом мы избавляемся от знака корня и получаем обычное уравнение 3-5х=243. Решив его, получаем х=-48. Задача решена.


На слайде 17 описывается решение уравнения 4√(8х+5)=-12. Чтобы решить данное уравнение, нужно вспомнить определение корня, которое также демонстрируется на слайде. Из него следует, что при возведении искомого числа в степень 4 должно получиться -12, а это невозможно, поэтому делается вывод о том, что уравнение не имеет корней.
На последнем слайде демонстрируется решение уравнения 3√(х2-х+2)=2. Также, как и во втором примере, для избавления от знака корня возводим в степень 3 обе части уравнения, сформировав равносильное уравнение. После преобразования получим обычное уравнение х2-х+2=8. Для решения применяется теорема Виета, в результате чего получаем корни уравнения х1=-2 и х2=3.
Презентация «Понятие корня n-й степени из действительного числа» дает возможность повысить эффективность школьного урока математики за счет улучшения наглядности представления учебного материала. Также наглядное пособие может пригодиться учителю, осуществляющему дистанционное обучение. Презентация может быть предложена для самостоятельного рассмотрения ученику, недостаточно хорошо усвоившему предмет.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5397 |
| Номер материала | 1017 |