
Презентация "Понятие определённого интеграла"

Краткое описание документа:
С помощью этой презентации по алгебре для 11-го класса мы рассмотрим понятие определенного интеграла, разберем несколько задач.
В предыдущей теме мы начали изучать неопределенный интеграл. Чтобы вспомнить это понятие и перейти к освоению нового урока, автор в начале презентации приводит определение неопределенного интеграла. Если функция y = f (x) имеет на интервале Xпервообразную y = F (x), то множество функций вида y = F (x) + С называют неопределенным интегралом от функции y = f (x) и обозначают соответствующим выражением, которое состоит из знака интеграла и подынтегральной функции f (x).

Перейдем к следующему слайду. Допустим, что функция y = f (x) является непрерывной на интервале от aдо b. Разобьем этот отрезок на nравных частей и составим сумму значений функции на этих отрезках. Вычислив предел суммы слагаемых, получим определенный интеграл. Другими словами, определенный интеграл от функции f (x) на интервале от a до b – это предел суммы большого числа слагаемых, где каждое из этих слагаемых стремится к нулю.

Таким образом, определенный интеграл отличается от неопределенного тем, что имеет пределы интегрирования. Отрезок от aдо bобычно называют отрезком интегрирования, буквой aобычно обозначают нижний предел интегрирования, а буквой b – верхний.
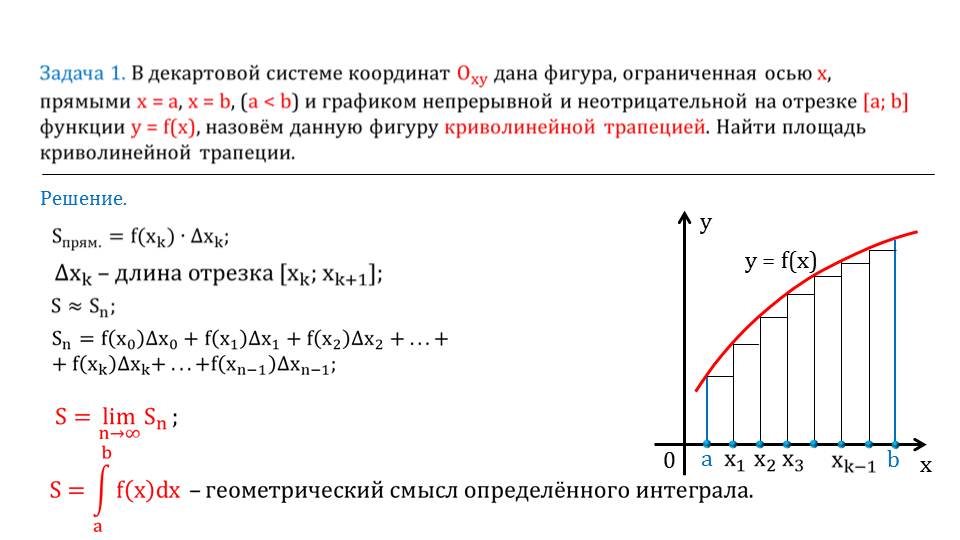
Рассмотрим такой пример (задача 1). В системе координат Оxyдана фигура, ограниченная осью абсцисс, прямыми x = a, x = b, причем a < bи графиком функции y = f (x). Эту фигуру мы можем назвать криволинейной трапецией. Необходимо найти ее площадь. Сделаем схематичный рисунок и разделим на нем криволинейную трапецию на прямоугольники. Площадь каждого прямоугольника можно вычислить как произведение значения
функции f(xk) на длину отрезка от xkдо xk+1. При условии, что количество прямоугольников стремится к бесконечности, площадь криволинейной трапеции становится равной сумме площадей прямоугольников, на которые она разделена. Т.е. мы можем вычислить предел этих слагаемых (площадей), а это и будет определенный интеграл.

Итак, мы узнали, что определенный интеграл имеет геометрический смысл: это площадь криволинейной трапеции, ограниченной отрезком на оси абсцисс, графиком функции y = f (x) сверху и прямыми x = a, x = b.
Перейдем к задаче 2. Дан прямолинейный стержень, где ρ = ρ (x) – это формула плотности в точке x. Необходимо найти массу стержня. Запишем формулу массы m = ρV. Аналогично предыдущему примеру, сделаем деление на равные отрезки. Тогда значение ρ на каждом отрезке оси xбудет равно ρ = ρ (xk), а значение массы на каждом отрезке будет равно произведению значения плотности ρ (xk) и длины отрезка. Всю массу стержня запишем как сумму масс на каждом отрезке. При бесконечном увеличении количества слагаемых всей массы стержня получим предел, т.е. определенный интеграл. Это физический смысл определенного интеграла.

В задаче 3 рассматривается еще один пример, когда определенный интеграл имеет физический смысл. Это расстояние, пройденное материальной точкой за промежуток времени от aдо b, когда v = v (t) – функция зависимости скорости от времени.

В конце презентации приводится пример. Скорость движения прямолинейной точки выражается как v = 1 + 2t. В момент времени t = 2 координата точки равняется 5, нужно найти закон движения. При решении находится расстояние с помощью определенного интеграла. Зная значения tи координаты C, можно найти закон движения.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3236 |
| Номер материала | 1037 |