
Презентация "Построение графиков прямой и обратной числовой функции"

Краткое описание документа:
Даная презентация посвящена теме «Построение графиков прямой и обратной числовой функции». Прежде чем переходить к рассмотрению данного урока, необходимо вспомнить определения обратимой и обратной функций.
Эти понятия были рассмотрены подробнее в предыдущей презентации, которую можно скачать и просмотреть. В настоящем уроке данные понятия выводятся на первых слайдах. Также предлагается вспомнить свойства прямой и обратной функций. Их всего 3 основных.


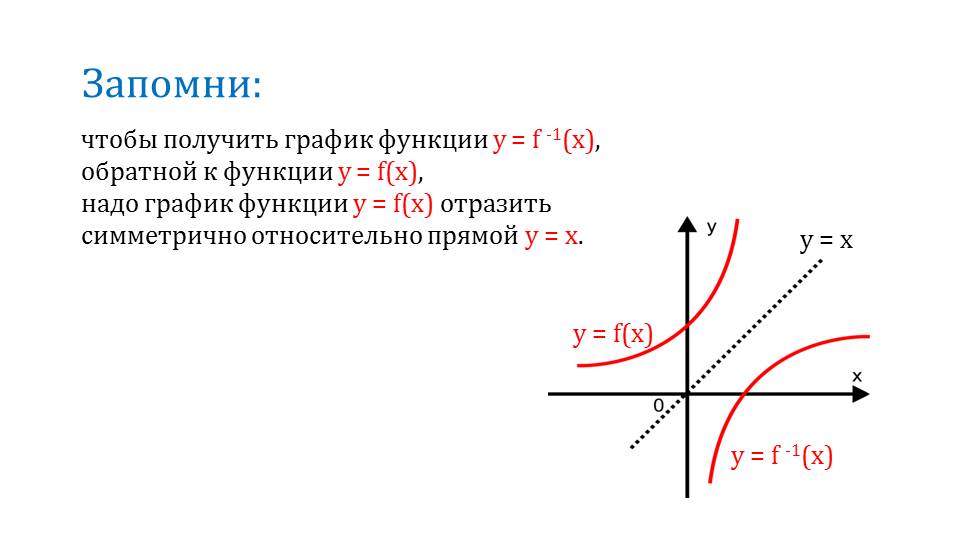
Первое свойство касается области определений, второе свойство – области значений, третье – монотонности. Значение аргумента х считается независимой переменной. А у – зависимой. На графике функции на иллюстрации демонстрируется график двух функций – прямой и обратной. Здесь наглядным образом можно увидеть характер изменения этих функций.
Можно обратить внимание, что эти функции являются симметричными относительно некоторой оси. Эта ось представляет собой график функции у=х. Таким образом можно получить обратную функцию для любой функции. Это определение дается на третьем слайде.

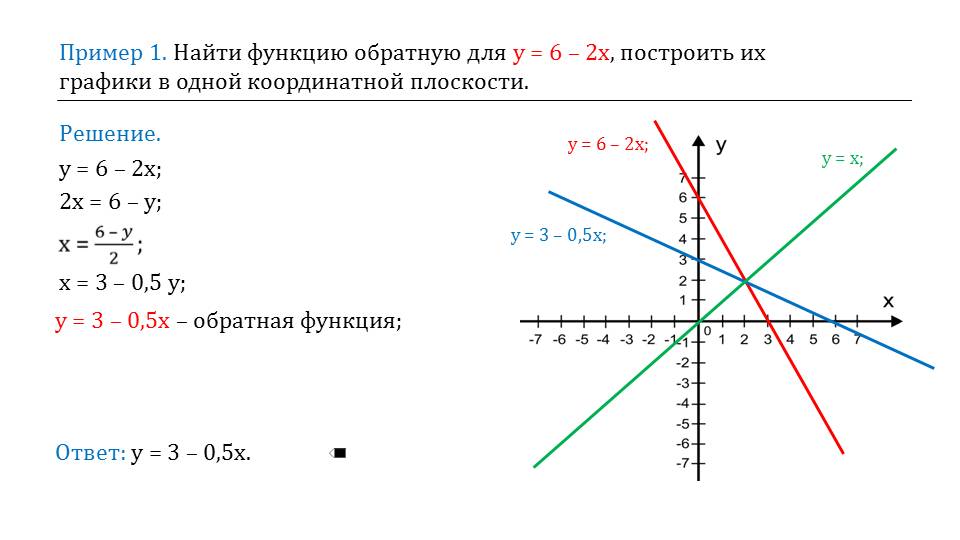
Далее предлагается рассмотреть пример. Имеется функция, графиком которой является прямая, то есть, имеем линейную функцию. Необходимо найти обратную к данной функции и построить график.
Решить задачу можно как алгебраически, так и геометрически. Для начала, из данного уравнения функции выражается в отдельности х, через у. То есть происходит замена зависимой и независимой переменных. Этот процесс изображается графически.
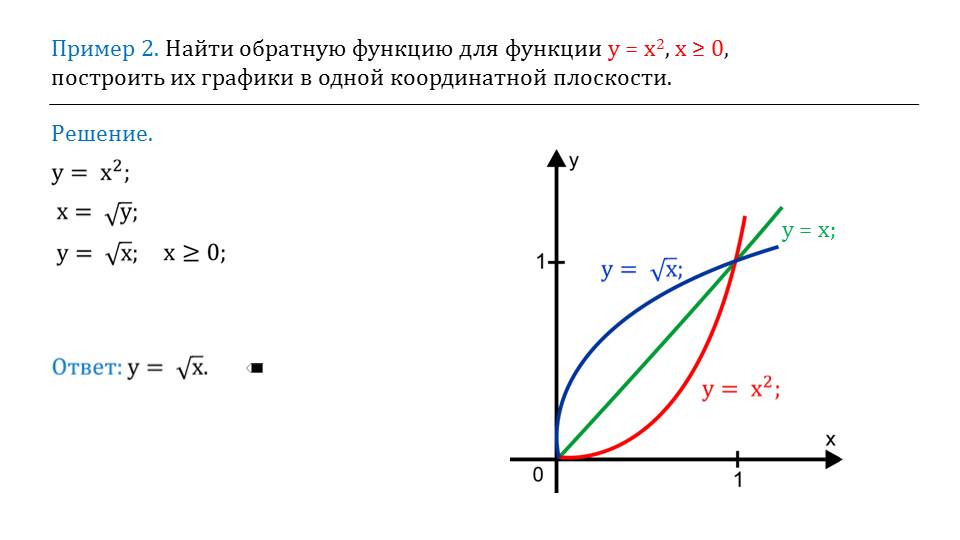
Можно заметить, что эти линии являются симметричны прямой, проходящей через точку О, которая задается уравнением х=у. Второй пример предлагает найти обратную функцию для функции, графиком которой является парабола. Предлагается рассмотреть исключительно положительную область. То есть ту область, на которой значения аргументов будут больше или равняться нуля. Аналогично предыдущему примеру, первым делом выражается х через у. Далее производиться замена. Также графически изображаются эти кривые.
На этом презентация подходит к логическому завершению. Школьник может самостоятельно попробовать найти обратную к другим функциям.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5535 |
| Номер материала | 782 |