
Презентация "Преобразование выражений, содержащих радикалы"

Краткое описание документа:
Презентация «Преобразование выражений, содержащих радикалы» является наглядным пособием для ведения школьного урока по данной теме. Задача такого урока – сформировать навыки применения свойств корня n степени для решения математических задач. Данная презентация помогает сформировать основные умения в решении задач, в которых необходимо уметь применять свойства корня. В ходе презентации вводится понятие иррациональных выражений, напоминаются формулы основных свойств корня nстепени.
Презентация очень удобна для наглядного представления учебного материала. В ней заранее подобраны примеры, которые наиболее удобно демонстрируют применение изученных свойств. На слайдах дается подробное описание решения, которое хорошо видно с любой парты в классе, что важно для учебного процесса. Анимационные эффекты и выделение части текста цветом помогают удерживать внимание учеников на процессе обучения. Определения и свойства, которые требуют запоминания, также выделяются цветом, заключаются в рамку, могут быть рекомендованы для запоминания.


Демонстрация начинается с представления определения иррационального выражения или выражения с радикалами. Отмечается, что такими выражениями являются выражения, содержащие корни. Определение заключается в рамку, понятие выделено цветом. Определение может быть рекомендовано под запись в тетради. На втором слайде напоминаются свойства корня nстепени. Демонстрируются 6 свойств:
- возведение в степень n корня степени n, то есть (n√a)n=n√an=a;
- корень произведения n√ab=n√a·n√b;
- корень частного n√a/b=n√a/n√b;
- возведение корня n степени в степень k, то есть (n√a)k=n√ak;
- корень степени n от корня степени k, то есть n √k√a=nk√a;
- возведение в одну степень подкоренного выражения и показателя степени np√akp=n√ak.

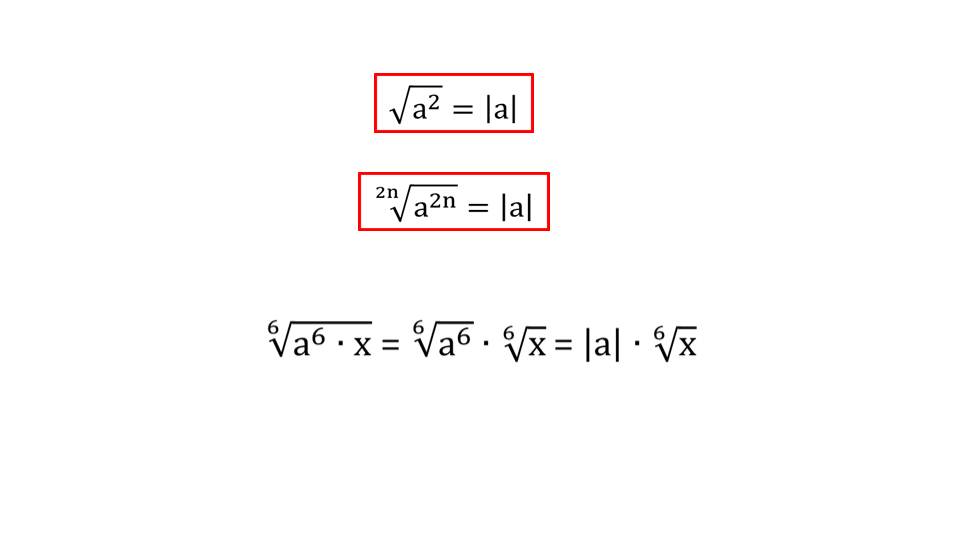
Далее рассматриваются примеры, для решения которых необходимо использовать изученный материало свойствах корня nстепени. В примере требуется упростить выражения 3√54а5 и (5√a3)4. В правой части экрана напоминаются формулы, которые понадобятся для решения примера – корень nстепени из произведения, а также возведение в степень корня некоторой степени. Упрощение первого выражения начинается с разложения произведения в подкоренном выражении на произведение более удобных множителей. По формуле преобразуем корень произведения в произведение корней. В результате вычисления записывается упрощенный вид выражения 3а·3√2·a2. Во втором случае формула прямо применяется для определения степени в подкоренном выражении, а затем упрощается. В результате вычислений получаем (5√a3)4=а2·(5√a2).
На четвертом слайде рассматриваются особенности применения некоторых свойств корня n степени. В первой формуле указывается, что корень квадратный из а в квадрате равно модулю √a2=|а|. Во второй формуле правило обобщается, распространяясь на все четные числа, то есть 2n√a2n=|а|. В качестве примера, демонстрирующего применение данного правило, описывается упрощение выражения 6√(a6·x)= 6√a6·6√x=|а|·6√х.
На слайде 5 описывается решение примера 2, в котором необходимо сравнить числа 24√5 и 54√2. В правой части слайда напоминается формула возведения в степень nкорня n степени. Для сравнения данных чисел они преобразуются так, чтобы множитель перед корнем попал в подкоренное выражение. Для этого целый множитель представляется в виде дроби и выражение преобразуется, получив 4√80. Таким же образом преобразуется второе выражение, приобретая вид 4√1050. Получив корень одинаковой степени, отмечаем, что больше то выражение, в котором больше подкоренное выражение, то есть 24√5<54√2.


На слайде 6 описывается решение примера 3, в котором необходимо упростить выражение 5√у4·3√у2. В правой части слайда напоминаются формулы корня произведения и извлечения корня из корня. Чтобы решить пример, сначала преобразуется подкоренное выражение – множитель перед корнем заносится под знак корня. Затем выражение преобразуется с помощью второй формулы. В результате получаем упрощенное выражение 15√у14.
В примере 4 необходимо выполнить действия (6√х-6√у)( 6√х+6√у). Очевидно, для преобразования этого выражения можно использовать формулу сокращенного умножения. В правой части слайда напоминается эта формула, а также еще две формулы, отображающие свойства корня и используемые для преобразования. После преобразования выражения с помощью формулы сокращенного умножения получается (6√х)2-(6√у)2. После применения для преобразования свойств корня, получаем упрощенное выражение 3√х-3√у. Задача решена.
Для решения примера 5 необходимо использовать четыре изученных свойства корня nстепени. Определяется значение выражения 7√у5·15√у8. Оба множителя сначала приводятся к виду, когда имеют одинаковый показатель степени корня. Затем они перемножаются в одном подкоренном выражении, а потом из-под корня выходит целая часть и выражение принимает окончательно упрощенный вид у105√у16. Задача решена.


Презентация «Преобразование выражений, содержащих радикалы» рекомендуется в качестве наглядного пособия для повышения эффективности традиционного урока математики по данной теме. Материал может использоваться как инструмент для объяснения учителем в ходе дистанционного обучения. При необходимости ученику самостоятельно освоить умения решать задачи с использованием корней, пособие может быть рекомендовано для домашней работы.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5926 |
| Номер материала | 1020 |