
Презентация "Простейшие задачи в координатах"

Краткое описание документа:
Тема «Метод координат» в разделе, изучающем векторы программы 9 класса, дает знания о важном методе решения геометрических задач. После того, как ученик освоит основы метода – формирование координат вектора, связь между координатами вектора и координатами его начала и конца, можно приступать к практической части данной темы – формирования навыка использования изученных знаний при решении задач на векторы. В данной презентации рассматриваются наиболее часто встречающиеся задачи, в которых требуется применить метод координат – поиск координат середины отрезка, длины вектора по координатам его начала и конца, а также расстояния между двумя точками. Умение решать подобные задачи очень важно. В презентации «Простейшие задачи в координатах» рассматривается подробное решение задач в общем виде, на основе имеющихся у девятиклассников знаний в области векторной алгебры.


Рассматривать типичные задачи целесообразно при помощи презентации. Так учитель имеет возможность сопровождать объяснение яркими построениями, с соответствующим выделением важных моментов, к тому же не теряя времени на математическое описание метода на доске. Это позволяет наладить эффективную обратную связь с учениками, не отвлекаясь на технические детали, а также сконцентрировать внимание учеников на изучаемом предмете.
В начале презентации демонстрируется название изучаемого метода, при помощи которого решается множество геометрических задач. Первая типовая задача связана с нахождением координат середины отрезка. Чтобы наглядно продемонстрировать геометрический смысл решаемой задачи, строится прямоугольная система координат, на которой отмечаются координатные векторы i и j. На координатной плоскости отмечаются точки А(х1,у1) и В(х2,у2). Данные точки являются концами отрезка АВ, который строится на плоскости. На отрезке отмечается точка С(х,у), являющаяся его серединой. Построив радиус-векторы ОА, ОС и ОВ, отмечается, что (OC) ⃗=1/2((OA) ⃗+(OB) ⃗), то есть радиус-вектор серединной точки будет равен половине суммы двух радиус-векторов, соответствующих концам отрезка. Чтобы определить координаты середины отрезка, отмечаются координаты радиус-векторов, соответствующих концам отрезка, а координаты радиус-вектора будут равными полусумме соответствующих координат х и у. Данный вывод формулируется внизу слайда и предназначен для запоминания учениками.
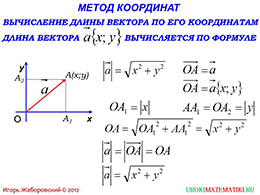
Третий слайд содержит объяснение правила вычисления длины вектора по координатам с подробным объяснением, как оно образуется. В начале слайда дается формула для вычисления длины вектора по координатам его концов. Объяснение сопровождается построением рисунка, где определяется длина радиус-вектора. На координатной плоскости отмечается точка А с координатами х и у. К ней проводится радиус-вектор (OA) ⃗, соответствующий вектору a ⃗. Координаты вектора a ⃗будут соответствовать координатам точки в конце вектора. Очевидно, что длина вектора a ⃗ будет соответствовать длине гипотенузы прямоугольника, катеты которого ОА1 и АА1, а гипотенуза ОА, так как АА1- перпендикуляр, опущенный из точки А на ось ОХ. Соответственно, длиной отрезка ОА1 будет модуль х, а длиной отрезка АА1 будет модуль ординаты у. По теореме Пифагора легко находим значение гипотенузы, которое равно квадратному корню из суммы квадратов координат х и у. Соответственно, длина вектора a ⃗ будет равна длине вектора (OA) ⃗, то есть длине отрезка ОА. Пришли к формуле, которая была дана в начале слайда. Она демонстрируется внизу слайда.

Еще одна типовая задача – на вычисление расстояния между точками. На системе координат отмечаются две точки М1 и М2, между которыми прокладывается отрезок. Его длину и необходимо измерить. Отмечается, что каждая из координат вектора ММ1 представляется как разность координат конца и начала отрезка. При этом длина вектора (MM_1 ) ⃗Определяется как извлеченный квадратный корень из суммы квадратов данных координат. Полученная формула демонстрируется в конце слайда.
Презентация «Простейшие задачи в координатах» может быть использована учителем на уроке для углубления знаний учеников о методах решения задач, расширенного понятия о применении метода координат. Презентация просто и понятно объясняет механизм применения данного метода, поэтому мжет быть полезна при самостоятельном изучении предмета девятиклассниками, а также при дистанционном обучении учеников.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6712 |
| Номер материала | 695 |