
Презентация "Разложение вектора по двум неколлинеарным векторам"

Краткое описание документа:
Презентация «Разложение вектора по двум неколлинеарным векторам» создана для сопровождения наглядным мультимедийным материалом темы урока геометрии в 9 классе раздела «Векторы». Умение раскладывать вектор по двум неколлинеарным необходимо учащимся для решения практических задач по данной теме. Презентация содержит лемму коллинеарности векторов и теорему о правилах разложения вектора по двум неколлинеарным векторам. Задача данной презентации – сформировать понятие учеников о коллинеарности векторов, формировать умение раскладывать вектор по двум неколлинеарным векторам, доказать правильность метода разложения.

Тема урока, заключенного в презентации, средней сложности. Проведение операций с векторами требует хорошего абстрактного мышления, глубокого понимания особенностей векторов и специфики проведения операций с ними. Нередко плохо сформированное математическое мышление становится проблемой в решении задач на векторы. Основное внимание в презентации обращается на подробное объяснение каждого процесса для формирования глубокого понимания предмета. Презентация содержит весь основной материал, взятый за основу в изучении данной темы в 9 классе с подробным объяснением и использованием инструментов презентации для облегчения понимания.
В данной презентации используются анимированные построения и вычисления, которые помогают лучше освоить материал. Также для изучения данной темы актуально выделение цветом основных понятий и утверждений, особенностей построения.
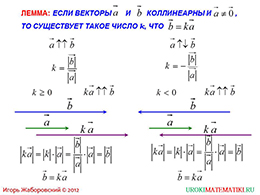
Презентация начинается с леммы коллинеарности векторов. Утверждение выделено синим цветом для облегчения запоминания. Рассматриваются оба случая – и векторов, направленных в одну сторону, и в противоположном направлении.


В колонке слева на слайде рассматривается случай коллинеарных векторов a ⃑ и b ⃑, направленных в одну сторону. Вводится обозначение коллинеарных, одинаково направленных векторов. Коэффициент коллинеарного вектора b ⃑ по отношению к a ⃑ определяется нахождением значения отношения длин данных векторов. Отмечается, что для одинаково направленных векторов такой коэффициент будет положительным или нулевым. Условие сопровождается графическим построением. Построен вектор b ⃑, ниже него заметно меньший a ⃑. При умножении вектора a ⃑ на коэффициент k, получается вектор, равный по длине вектору b ⃑. Ниже рисунков расписано, как образуется вектор b ⃑ умножением вектора a ⃑ на коэффициент k. При подстановке коэффициента k, равного отношению длин двух векторов для перемножения с вектором a ⃑, после сокращения одинаковых значений числителя и знаменателя, получаем значение вектора b ⃑. Справа расписывается случай противоположно направленных векторов. Также вначале обозначаются противоположно направленные коллинеарные векторы, а затем отмечается, что коэффициент коллинеарных векторов при делении длин вектора b ⃑ на вектор a ⃑ будет отрицательным. Ниже отмечается коллинеарность одинаково направленных векторов ka ⃑ и вектора b ⃑. Объяснение сопровождается рисунками векторов, где a ⃑ и b ⃑ противоположно направлены, а ka ⃑, повернутый в противоположную сторону к a ⃑ , благодаря умножению на отрицательный коэффициент, будет одинаково направленным к b ⃑. Подставив в произведение |ka ⃑ | коэффициент как отношение длин векторов b ⃑ и a ⃑, получаем верное равенство b ⃑=ka ⃑. Таким образом, рассмотрен случай представления вектора через коллинеарный ему.
В задачах векторной алгебры часто необходимо разложить вектор p ⃑ по неколлинеарным векторам a ⃑ и b ⃑. Правило разложения вектора по двум неколлинеарным векторам заключено в формуле p ⃗=xa ⃗+yb ⃗, то есть разложение вектора по двум неколлинеарным векторам, производится умножением каждого из векторов на определенный коэффициент и сложением их. При этом обозначено, что x и y называются коэффициентами разложения.
На следующем слайде приводится утверждение о том, что любой вектор раскладывается по двум неколлинеарным векторам. Логично переходя от изученного понятия о том, что коллинеарные векторы отличаются только коэффициентом, отмечается, что в выражении, которое представляет разложение вектора по двум неколлинеарным векторам в общем виде, коэффициент первого вектора просто равен нулю. Если же векторы не коллинеарные, оба коэффициента ненулевые. Справа в колонке раскрывается геометрический смысл данного правила. После сбора начала векторов в одну точку, Из конца вектора p ⃑ на прямую, образованную вектором a ⃑ опускается линия, параллельная вектору b ⃑. Образуется вектор (〖ОА〗_1 ) ⃗ , коллинеарный вектору a ⃑. Также образуется вектор (A_1 P) ⃗ , коллинеарный вектору b ⃑. Вектор p ⃑ получается суммированием по правилу параллелограмма данных векторов, коллинеарных исходным. Таким образом раскрывается смысл каждой части выражения и общий геометрический смысл проведенной операции разложения данного вектора по двум неколлинеарным.

На следующем слайде доказывается исходное утверждение о единственной возможности разложить вектор по данным двум неколлинеарным векторам. Как наиболее наглядный, выбирается способ доказательства от противного. Отмечается доказанное выражение, соответствующее требованиям разложения вектора по двум данным неколлинеарным векторам. Ниже указывается допущение, что существует еще одно разложение по данным векторам. Так как векторы используются те же самые, данные выражения могли бы отличаться только коэффициентами при них. Для поиска различия из первого выражения вычитается второе, общие множители выносятся за скобки. В результате получается, что разность соответствующих коэффициентов обоих выражений будет равной нулю. Но в этом случае для результирующего вектора такое отношение не имеет смысла, так как в знаменателе не может быть нуль. А так как это свидетельствует о коллинеарности a ⃑ и b ⃑, полученный результат противоречит условию утверждения.
Данная презентация содержит детальное объяснение сложных для школьника понятий, поэтому может быть рекомендована не только как мультимедийное пособие учителя на уроке, но и для самостоятельного изучения темы, использована для дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9856 |
| Номер материала | 692 |