
Презентация "Решение квадратных неравенств" Часть 2

Краткое описание документа:
Презентация «Решение квадратных неравенств» часть 2 - мультимедийное пособие, созданное в помощь учителю на уроке алгебры в 8 классе по теме «Решение квадратных неравенств». При помощи презентации учитель продолжает формировать умение учащихся решать квадратные неравенства. Рассматривая различные способы решения квадратных неравенств, в данной презентации уделяется внимание решению неравенств с использованием свойств, изложенных в теореме о знаке неравенства при отрицательных дискриминанте и старшем коэффициенте. Навыки в решении квадратных неравенств закрепляются решением задач различными способами.

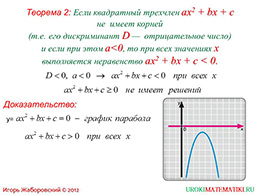
слайды 1-2 (Тема презентации "Решение квадратных неравенств. Часть 2", теорема)
Использование презентации на уроке алгебры позволяет сократить затраты времени учителя на подготовку материала для объяснения ученикам, построение графиков, выделение основных понятий. Все действия, занимающие время урока, упразднены. Наглядность обеспечена заранее – выделены цветом основные понятия, структурировано объяснение, графики не просто построены, но и все необходимые части выделены и обозначены разными цветами, помогая запомнить и более глубоко понять особенности процесса.
Презентация начинается с формулировки теоремы о том, что значения квадратного трехчлена лежат в отрицательной полуплоскости, если дискриминант и старший коэффициент имеют отрицательное значение. Условия и заключение теоремы выделены красным, акцентируя внимание на них и улучшая запоминание материала. Далее указано, что при таких условиях в положительной полуплоскости трехчлен не имеет значений и соответствующее неравенство не имеет смысла.
Доказательство данной теоремы не приводится в презентации. Оно обозначено только схематически – можно увидеть график и начало доказательства. Если есть возможность углубить изучение темы и доказать утверждение, это делается вне презентации на уроке или на дополнительном занятии, используя данную схему.

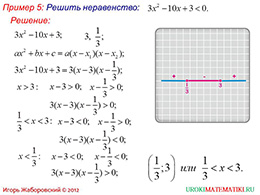
слайды 3-4 (примеры)
Далее для закрепления изученного материала приводится пример на решение неравенств. Первое неравенство подобрано с положительным старшим коэффициентом, а второе – с отрицательным. В ходе решения выделяется квадратный трехчлен, затем находится его дискриминант. Получив отрицательное значение дискриминанта, делается вывод о положительном значении данного трехчлена на всей числовой оси x.
В ходе решения второго неравенства выясняется, что дискриминант отрицательный, а старший коэффициент также отрицательный. Зная свойство квадратного трехчлена по теореме, замечаем, что все значения данного трехчлена лежат в полуплоскости отрицательных значений, поэтому данное неравенство решений не имеет.
Далее демонстрируется пример 5, где необходимо решить неравенство, анализируя наложение промежутков на числовой оси. Имея навыки решения квадратного уравнения, находим решения, которые помогают его разложить на множители. Чтобы неравенство было верным, демонстрируется, что множители должны иметь разные знаки. Если знаки будут одинаковыми, то неравенство не соблюдается. Если x лежит между 1/3 и 3, неравенство будет верным. В иных случаях значения становятся отрицательными. Во время демонстрации решения и анализа ход рассуждений отслеживается по рисунку, где обозначены промежутки отрицательных и положительных значений.

слайд 5 (пример)
В последнем примере рассматривается решение квадратного неравенства методом интервалов. Это уравнение непростое в решении. Для его решения ученику необходимо обобщить свои знания и использовать умение решать квадратные неравенства. Успешное решение обнаружит глубокое понимание материала и умение анализировать.
Данный пример может быть рассмотрен и в ходе объяснения учителя. Необходимо повторить признак наличия и количества корней уравнения, а затем вывести выражение для вычисления дискриминанта. Зная, что положительный дискриминант – это два корня уравнения, решение (а) сводится к решению квадратного неравенства 25-4p^2>0. Так же для единственного решения дискриминант должен равняться нулю, и решение сводится к поиску корней уравнения 25-4p^2=0. Корней уравнения нет, если дискриминант отрицательный.
Для поиска решения необходимо решить неравенство 25-4p^2<0. Демонстрируется решение данной задачи. На рисунке можно отслеживать промежутки значений, характерные для каждого решения.
При помощи данной презентации углубляются знания по теме «Решение квадратных неравенств», закрепляются навыки в решении задач с использованием квадратных неравенств. Презентация может быть использована на уроке, а также при самостоятельном изучении, в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5793 |
| Номер материала | 316 |