
Урок "Исследование функции на монотонность"

Краткое описание документа:
В повседневной жизни часто приходится наблюдать множество процессов и явлений, при изучении которых нужно рассматривать самые разнообразные величины. Эти величины могут по-разному зависеть друг от друга. Закон, по которому одна величина зависит от другой, мы назвали функцией. Это одно из основных математических и общенаучных понятий, имеющее практическое применение во многих областях знаний и человеческой деятельности. Поэтому так важно уметь исследовать функции.
В данном видео уроке познакомимся с правилами исследования известных нам функций на монотонность.
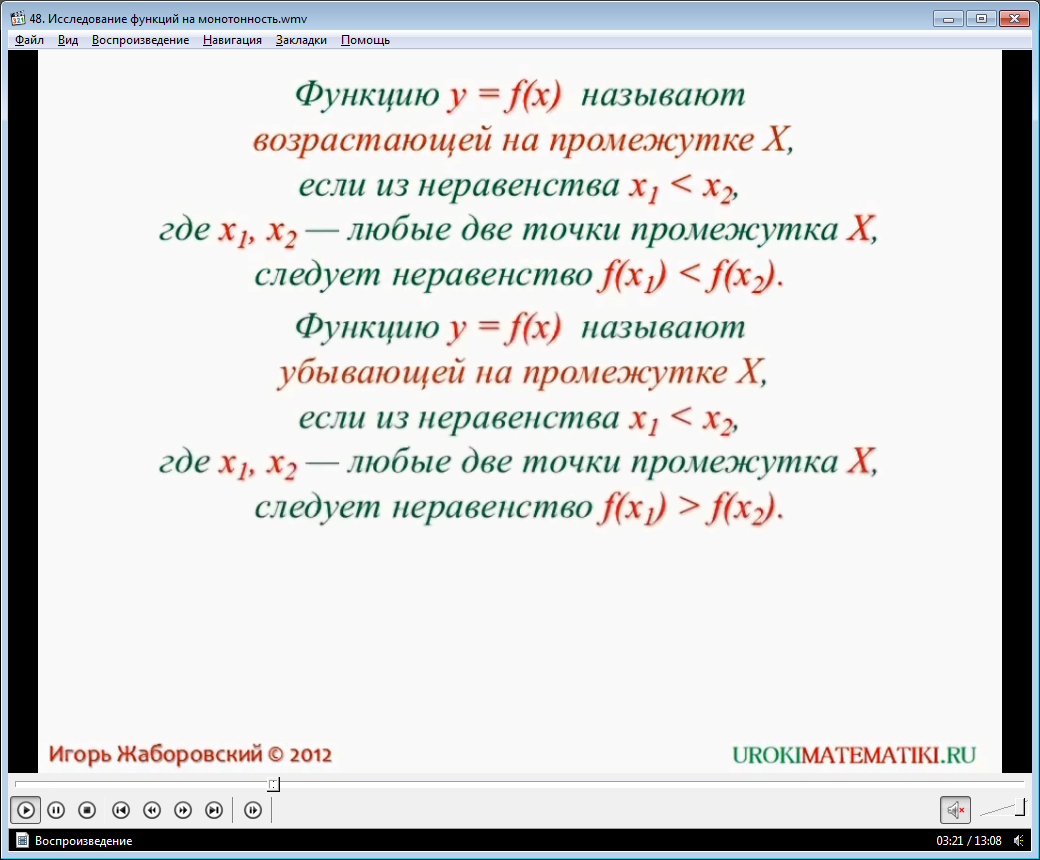
Разглядывая графики, мы уже многое можем сказать об их функциях. Например, указать возрастает функция или убывает, как об этом говориться в видео уроке. Однако понятия возрастания и убывания функций в математике имеют свои точные определения, которые и приведены в предложенном нашему вниманию видеоматериале.
Так, чтобы судить о возрастании или убывании функции, зададим некоторый промежуток, на котором будем исследовать функцию. В видео уроке это промежуток Х. Выберем любые два числа, принадлежащие промежутку Х. Пусть это будут числа х1 и х2. Эти два числа являются двумя значениями аргумента, которым соответствуют два значения какой-либо функции f(x1) и f(x2). Если получается, что при х1 > х2 выполняется неравенство f(x1) > f(x2), то наша функция возрастает на промежутке Х.
Другими словами, можно сказать, что функция f(x) называется возрастающей на данном числовом промежутке Х, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Аналогично в видео уроке рассматривается понятие убывающей функции.
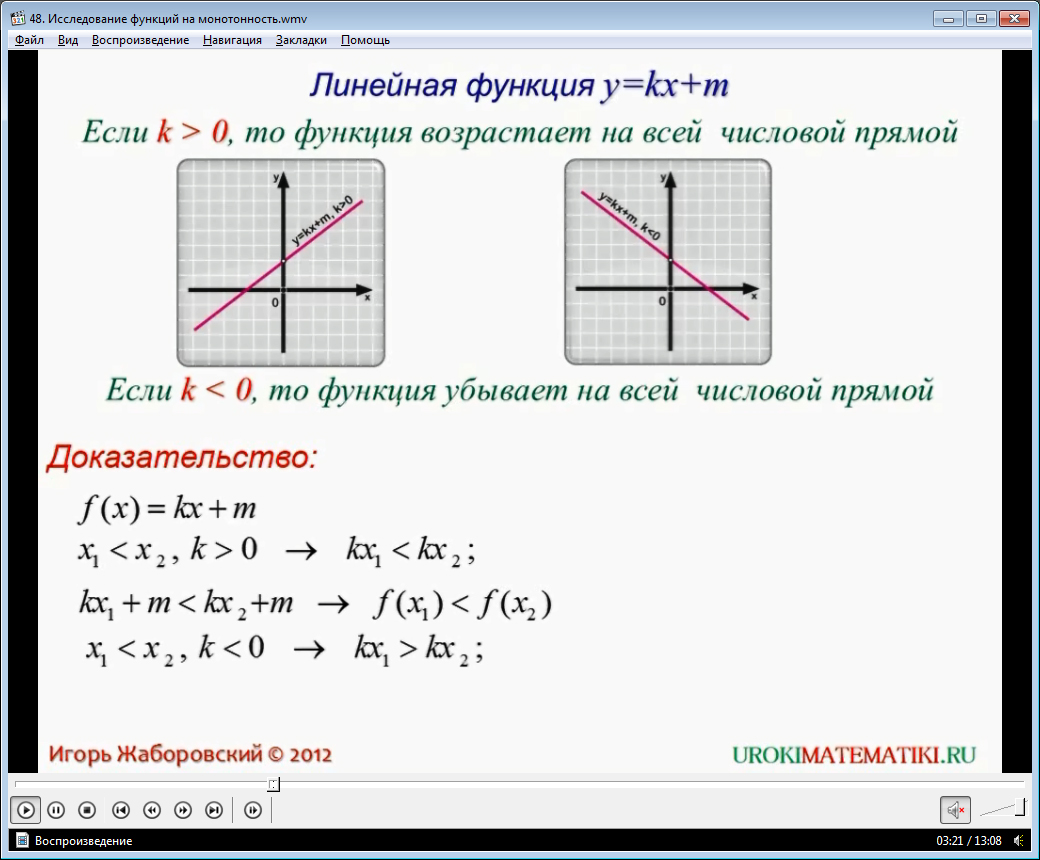
Далее в видеоматериале подробно проводится исследование линейной функции y = kx + m. Как известно, эта функция определена на всем множестве действительных чисел, то есть на всей числовой прямой. Даже если не проводить математических доказательств, а просто судить по графику этой функции, видно, что она ведет себя одинаково на всей области определения. Функция либо возрастает (график все время идет вверх), либо убывает (график все время идет вниз). В таких случаях можно не указывать промежуток, а просто сказать, что функция возрастающая или убывающая.
Возрастает или убывает функция y = kx + m, зависит от коэффициента k. Если коэффициент k положительный, то функция y = kx + m возрастает на всей области определения, то есть является возрастающей. Если коэффициент k отрицательный, то функция убывает. Доказательство возрастания или убывания функции y = kx + m основано на свойствах числовых неравенств и рассматривается в видео уроке.
Обычно, если функция только возрастает или только убывает на данном числовом промежутке, то ее называют монотонной на этом промежутке. Функция y = kx + m монотонна на всей своей области определения.
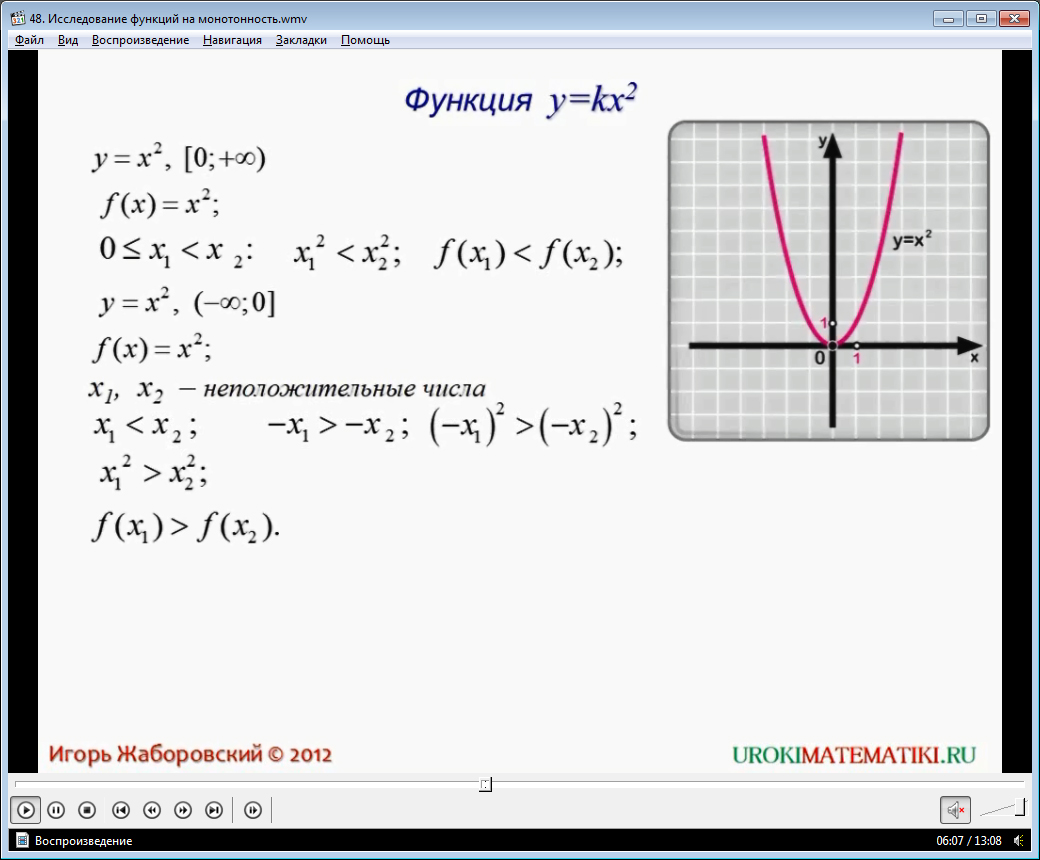
Следующая функция, которая рассматривается в видео уроке квадратичная y = kx2. Как и в первом случае, областью ее определения являются все действительные числа x. По графику мы видим, что функция ведет себя неодинаково. К тому же коэффициент k может быть, как положительным, так и отрицательным. Пусть коэффициент k больше нуля. Тогда если аргумент принадлежит промежутку (-∞; 0], то функция убывает. А вот на числовом промежутке [0; +∞) функция возрастает. Доказательство возрастания и убывания функции на соответствующих числовых промежутках, основанное на свойствах числовых неравенств, и с учетом знака коэффициента k, приведено в видео уроке.
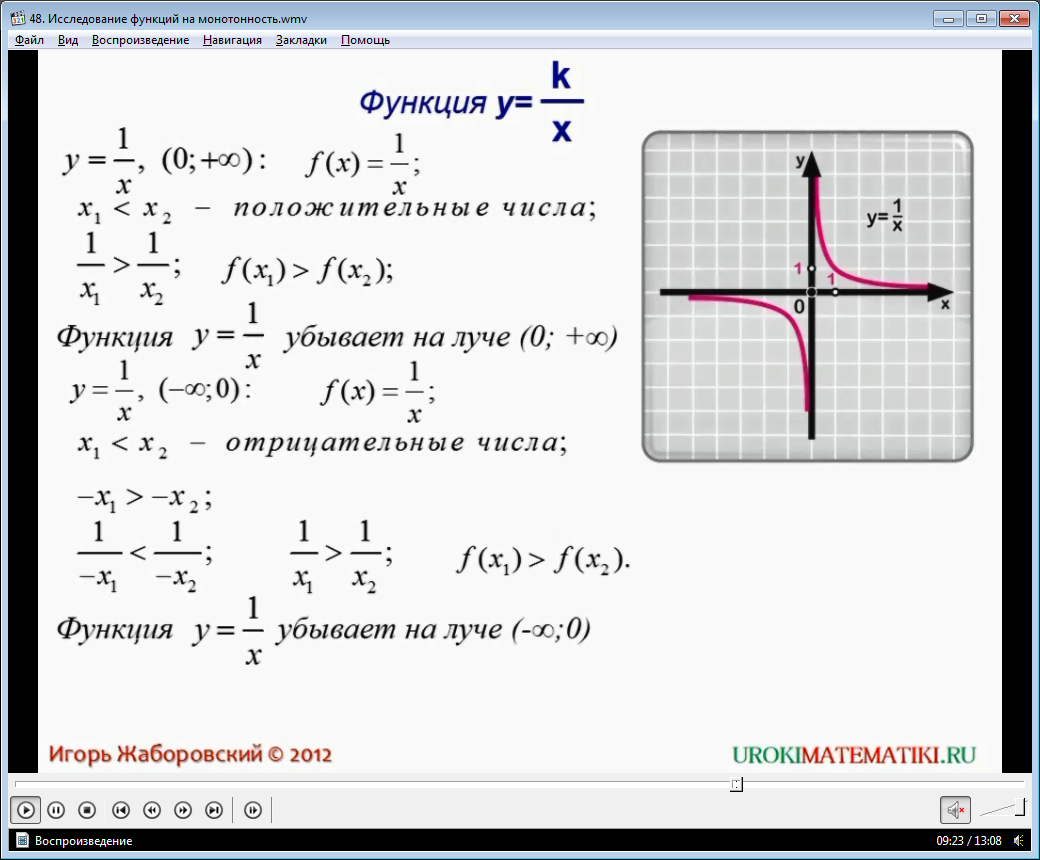
Переходим к рассмотрению функции y = k/x. Это график обратной пропорциональности. Он не является непрерывной линией. Действительно, x не может равняться нулю. Поэтому рассматриваем функцию на промежутках (-∞; 0) и (0; +∞). Графиком обратной пропорциональности является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Она называется гиперболой. Расположение ветвей гиперболы, а также возрастание или убывание функции на соответствующих промежутках, зависит от знака коэффициентаk. Подробно и доказательно поведение гиперболы показано в видеоматериале.
Еще одна функция, которую рассматривают видео уроке это y = √x. Доказывается, что она является возрастающей.
Завершает видео урок пример построения графика и исследования функции, которая на разных участках числовой оси задается разными формулами.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9777 |
| Номер материала | 570 |