
Урок "Решение квадратных неравенств" Часть 1

Краткое описание документа:
При изучении разделов алгебры, неравенства занимают значительную часть. Многие прикладные задачи можно решить, только используя неравенства.
Для решения квадратных неравенств необходимо понимание сути этого понятия. Под понятием «квадратное неравенство» следует понимать неравенства вида ax2+bx+c >0, ax2+bx+c<0, ax2+bx+c ≤0, а так же ax2+bx+c ≥0 при а≠0. Именно об этом и говорится в начале представленного видео урока.
В самом начале предложено рассмотреть все типажи квадратных неравенств на примерах одного квадратного трехчлена в левой части неравенства, а именно x2-2x-3.
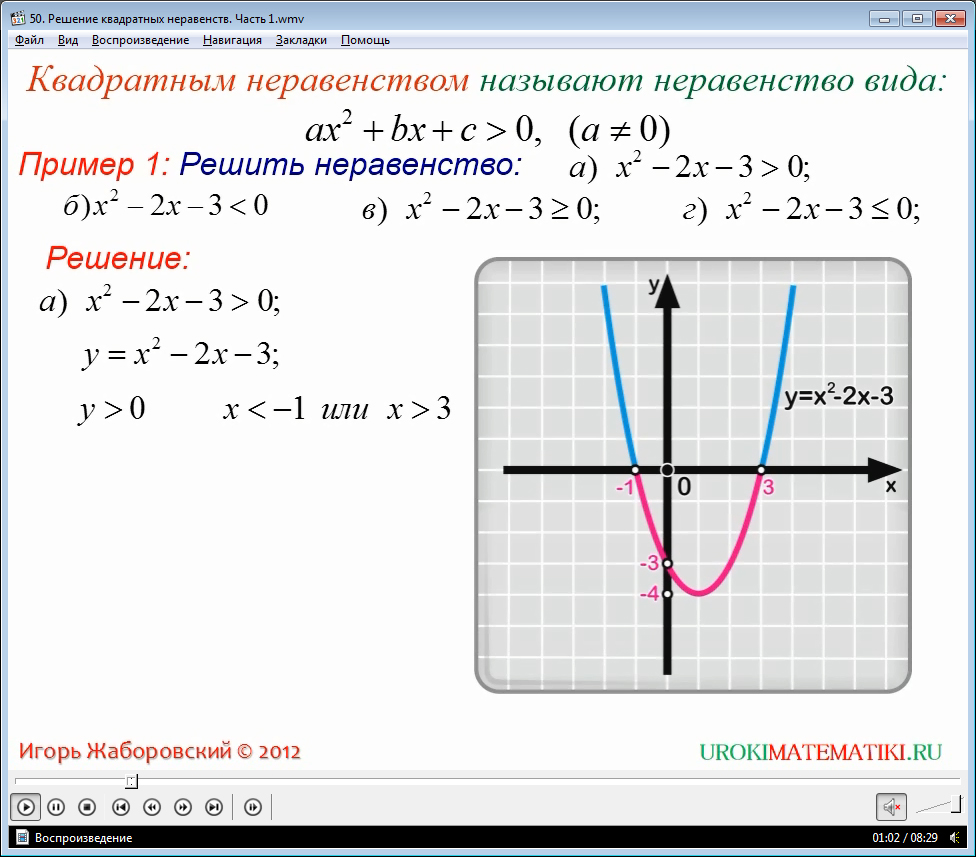
Первым рассмотрено решение неравенства x2-2x-3>0. При этом решение неравенства сводится к рассмотрению точно построенной параболы y=x2-2x-3. Навыки построения графика квадратичной функции к этому моменту должны быть сформированы у пользователей видео.
Чтобы решить предложенное неравенство, нужно определить при каких значениях переменной х точки параболы у=х2-2х-3 находятся выше оси абсцисс.
Замечено, что у>0, то есть график параболы расположен в верхней полуплоскости прямоугольной системы координат, при х<-1 или x>3.
Значит, решением неравенства рассматриваются все значения переменной х двух лучей: (-∞; -1) и (3;+ ∞). Ответ в конечном виде имеет смысл записать так: (-∞; -1)(3;+ ∞).
Далее рассматривается неравенство x2-2x-3<0. При этом рассматриваем ту же параболу, но в качестве решения берем только ту часть графика, которая расположена ниже оси х. Значения у меньше 0, если х больше -1 и меньше 3. Решением данного неравенства станет интервал (-1;3).
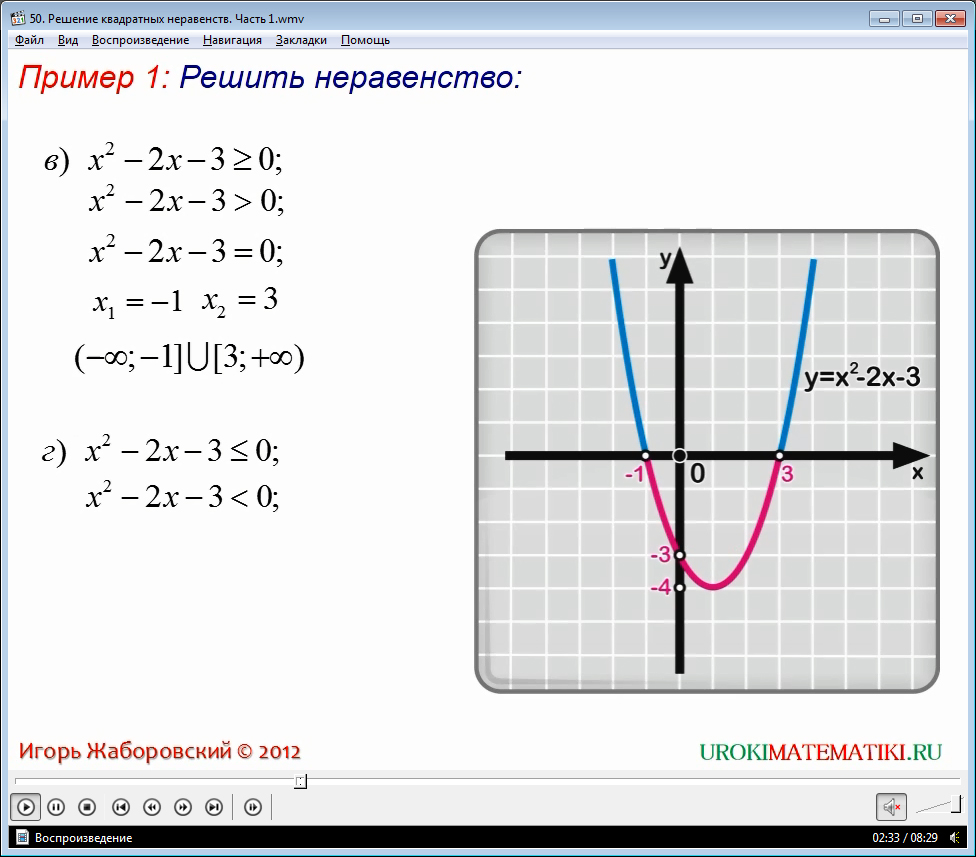
В третьем примере рассмотрено неравенство x2-2x-3≥0. Данное неравенство отличается от неравенства x2-2x-3>0 только строгостью неравенства. Поэтому и корни квадратного уравнения x2-2x-3=0 включаются в ответ.
Значит, решением этого неравенства будут все значения переменной х, входящие в объединение лучей (-∞; -1]∪ [3;+ ∞).
Последним из примеров рассмотренорешениенеравенства x2-2x-3≤0. Как и в предыдущем примере в ответ необходимо добавить корни квадратного уравнения x2-2x-3=0, х=-1 и х=3.
Таким образом, решением неравенства станут все точки отрезка [-1;3].
В видео здраво замечено, что при решении неравенства не имеет значения точность построения параболы, а только положение параболы относительно оси х. Поэтому строить параболу можно и схематически. Для этого достаточно найти корни квадратного трехчлена (точки пресечения параболы с осью х) и определить направление веток параболы. Ось у при этом изображать нет необходимости.
Схему решения квадратичного неравенства рассмотрено на примере неравенства: -2х2+3х+9<0.
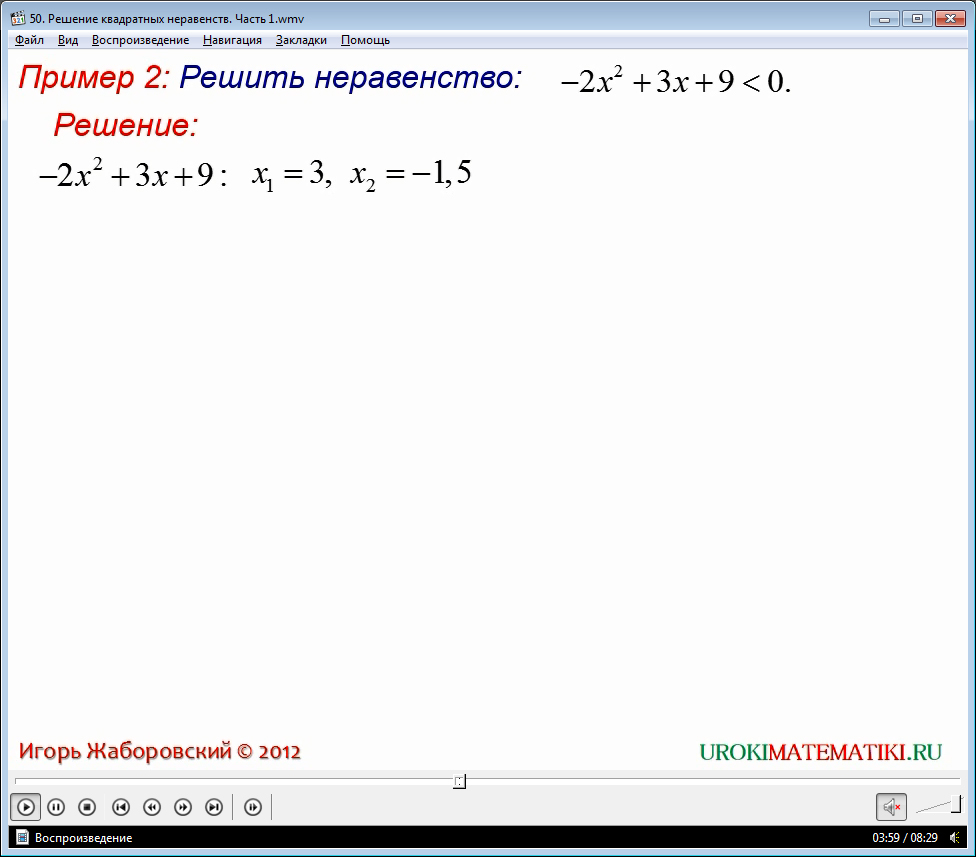
Представленная схема состоит из следующих пунктов:
1. Находим корни квадратного трехчлена -2х2+3х+9. Это х=3 и х=-1,5. Значит парабола пересекает ось х в точках 3 и -1,5.
2. Определяем направление ветвей параболы по значению коэффициента а. а=-2 - значит ветви направлены вниз. Схематически изображаем нашу параболу на рисунке.
3. Теперь мы можем сделать вывод о виде нашего ответа: у меньше 0 на тех участках оси х, где график ниже оси х. Это объединение открытых лучей (-∞;-1,5)∪(3;+∞).
Далее рассмотрен пример решения неравенства 4х2-4х+1≤0, когда квадратный трехчлен имеет один корень, то есть парабола касается оси х в одной точке х=0,5.
Используя описанную выше схему, определяем, что ветви параболы направлены вверх, парабола находится выше оси х во всех точках, кроме точки касания х=0,5.
Значит, решением неравенства может быть только значение х=0,5, в остальных случаях значения ординаты точек параболы положительны.

Рассмотрев все предложенные случаи квадратных неравенств, вырабатываем алгоритм решения неравенства:
1. Найти корни квадратного трехчлена ax2+bx+c.
2. Отметить найденные корни на оси х и определить направление ветвей параболы, служащей графиком функции y=ax2+bx+c, сделать схематический рисунок графика.
3. С помощью наброска определить ответ.
Но в случае, если квадратный трехчлен не имеет корней, алгоритм применить не получится.
В этом случае необходимо руководствоваться следующей теоремой.
Теорема 1. Если квадратный трехчлен ax2+bx+c не имеет корней и если при этом а>0, то при всех значениях х выполняется неравенство ax2+bx+c >0.
Доказательством этого может служить положение параболы, соответствующей данному неравенству, выше оси х при всех значениях х, что наглядно продемонстрировано в видео.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6142 |
| Номер материала | 572 |