
Урок "Решение линейных неравенств"

Краткое описание документа:
В этом видеоматериале пойдет речь о решении неравенств, которые имеют переменную. Они так и называются – неравенствами с одной переменной. Что же является решением таких неравенств? Это такие значения переменной, при которых решаемое нами неравенство становится верным числовым неравенством. А решить неравенство с переменной – значит найти все его решения или доказать, что их нет. Для нахождения этих решений мы используем свойства числовых неравенств, которые рассматривались ранее.
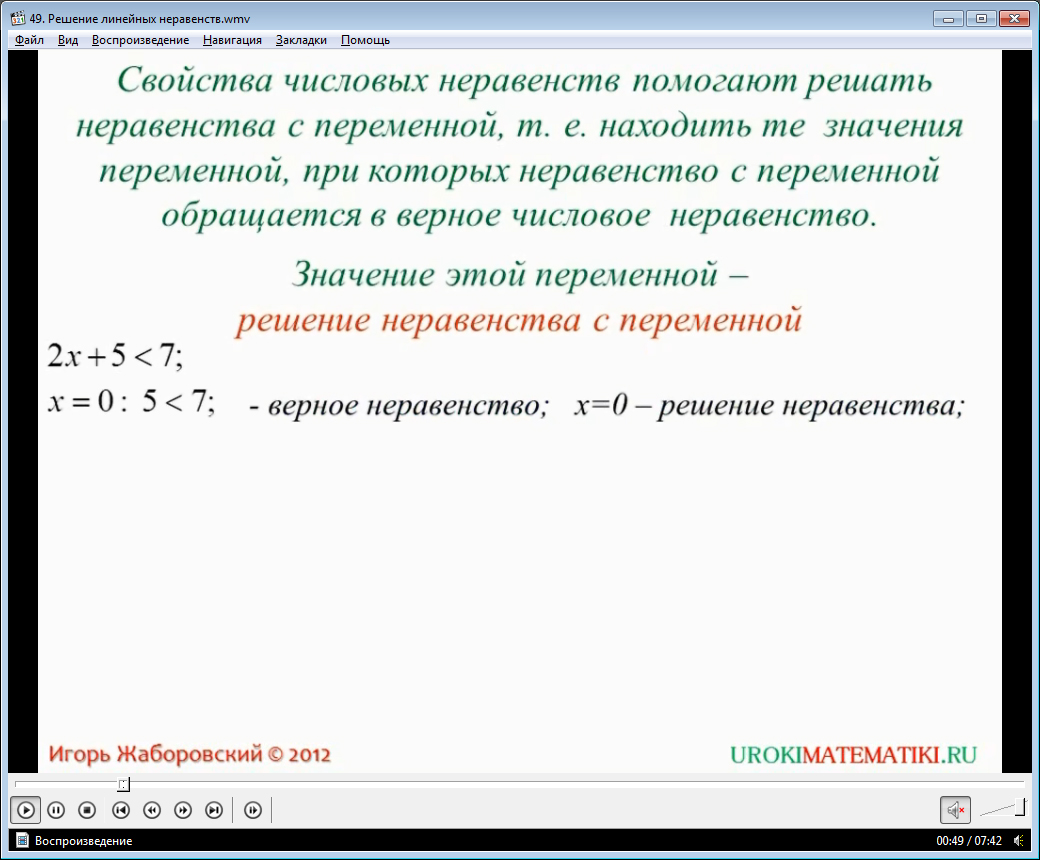
Рассмотренный в видео уроке простой пример показывает, как важно иметь четкий алгоритм решения, иначе говоря, знать правила решения неравенств.
Вот предлагается простое неравенство 2х + 5 < 7. Представим себе, что алгоритма решения у нас нет. Значит, мы будем перебирать все числа и смотреть, какие из них нам подходят, то есть при каких значениях переменной х данное неравенство станет верным числовым неравенством. Просматривая видео, замечаем, что подстановка одних чисел дает нам верное числовое неравенство, а подстановка других этого не дает. Приведенный пример показывает неэффективность данного способа решения.

Обратимся к свойствам числовых неравенств. Мы знаем, что к обеим частям неравенства можно прибавить одно и то же число. От этого неравенство не изменится. Также мы знаем, что обе части неравенства можно делить или умножать на одно и то же положительное число. В видео уроке показано, как, используя эти свойства, можно найти решение заданного неравенства. Получилось, что х < 1. Это значит, что все числа х, меньше единицы, являются решением неравенства. Они образуют открытый промежуток от минус бесконечности до единицы (числовой луч). Другими словами, у нас есть множество решений заданного неравенства. Окончательное решение неравенства можно записать, используя такие формы.
Первая форма записи: х < 1 (х меньше единицы).
Вторая форма записи: х Є (-∞; 1) (х принадлежит промежутку от минус бесконечности до единицы).
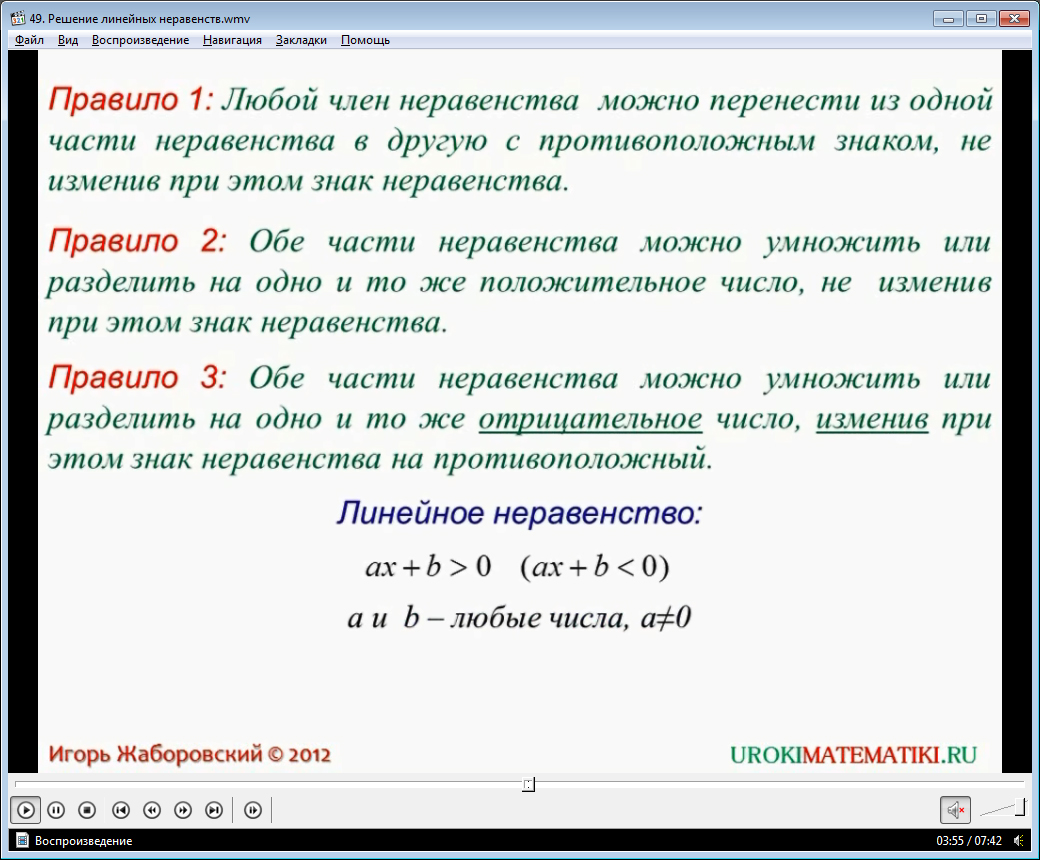
На основании рассмотренных ранее свойств числовых неравенств, можно сформулировать правила, с помощью которых решаются неравенства с одной переменной. Эти правила сформулированы в настоящем видео уроке.
Неравенства с одной переменной вида ах + b > 0 или ах + b < 0 называются линейными неравенствами. Неравенства могут также быть нестрогими, то есть содержать знак ≥ или ≤.
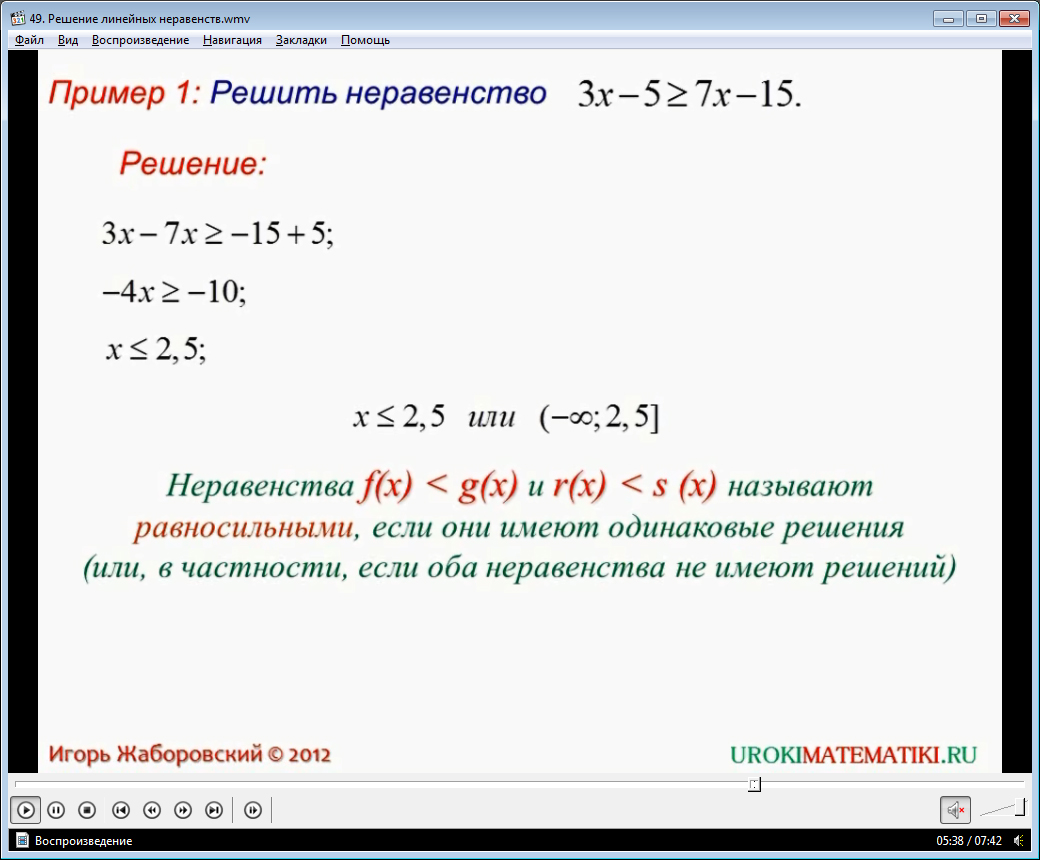
Далее в видеоматериале предложено рассмотреть решение линейного неравенства
Зх - 5 ≥ 7х - 15.
Для решения неравенства применяются уже известные нам правила. Сначала члены, содержащие переменную, собираем в левой части. При переносе из правой части в левую часть, слагаемое 7х, меняет знак. Числовые члены неравенства собираем в правой части, опять же не забывая менять знаки.
Далее придется разделить обе части неравенства на отрицательное число -4. В результате такого деления получается неравенство противоположного смысла. Обратите внимание, что в ходе решения мы постоянно пользуемся правилами решения неравенств. Окончательно получается, что х ≤ 2,5. Решение можно записать, используя любую из форм:
1. х ≤ 2,5 (х меньше либо равен 2,5);
2. х Є (-∞; 2,5] (х принадлежит промежутку от минус бесконечности до 2,5).
При изучении уравнений было рассмотрено понятие об их равносильности. Для неравенств тоже существует это понятие. Два неравенства с одной переменной будут равносильными, если решения этих неравенств совпадают. Если неравенства не имеют решений, то они также являются равносильными.
Существование равносильных неравенств позволяет намного упростить решение. Ведь тогда неравенство можно заменить равносильным ему, но более простым неравенством.
С помощью таких равносильных преобразований решается пример 2 настоящего видео урока.
| Автор | |
|---|---|
| Дата добавления | 31.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5290 |
| Номер материала | 571 |