
Презентация "Решение неравенств с одной переменной"

Краткое описание документа:
Презентация «Решение неравенств с одной переменной» наглядно представляет учебную информацию по данной теме на уроке математики. Изучив различные виды функций, их свойства, методы решения разных уравнений, можно обобщить сведения о решении неравенств, в состав которых входят выражения различного типа. С помощью презентации учителю легче произвести обобщение, дать информацию, требующую запоминанию, достичь учебных целей, повышая общую эффективность урока математики.




Сначала ученикам представляются сведения о том, что такое решение неравенства. Общее понятие решения неравенства вида f(x)>g(x) – значение его переменной х, обращающей неравенство с данным числовым значением в верное. Определение выделено в рамку, понятие решения окрашено красным цветом для лучшего запоминания. Также перед обобщением методов решения неравенств напоминается понятие равносильных неравенств. Отмечается, что равносильными есть неравенства f(x)>g(x) и р(x)>h(x), решения которых совпадают. Примером равносильных неравенств служат х>1 и х3>1.
На слайде 4 представлено еще одно важное понятие – следствие неравенства. Оно означает неравенство р(x)>h(x), решение которого совпадает с решением f(x)>g(x). Определение выделено в рамку и понятие предложено запомнить. Примеры следствия неравенств приводятся на слайде 5. Для неравенства log3(x-3)<1 следствием является неравенство х-3>0. Решив его, получается промежуток (3;+∞), при подстановке которого определяются решения неравенства log3(x-3)<1 – промежуток (3;6).




Далее представлена теорема о равносильных неравенствах. Нередко преобразование неравенства в равносильное помогает найти лучший способ решения исходного неравенства. Теорема утверждает, что при переносе члена неравенства в другую его часть с изменением знака члена неравенства на противоположный и сохранением самого знака неравенства, получается неравенство, равносильное исходному. Приводится пример равносильных неравенств – х2-7>=9х и х2-9х>=0.
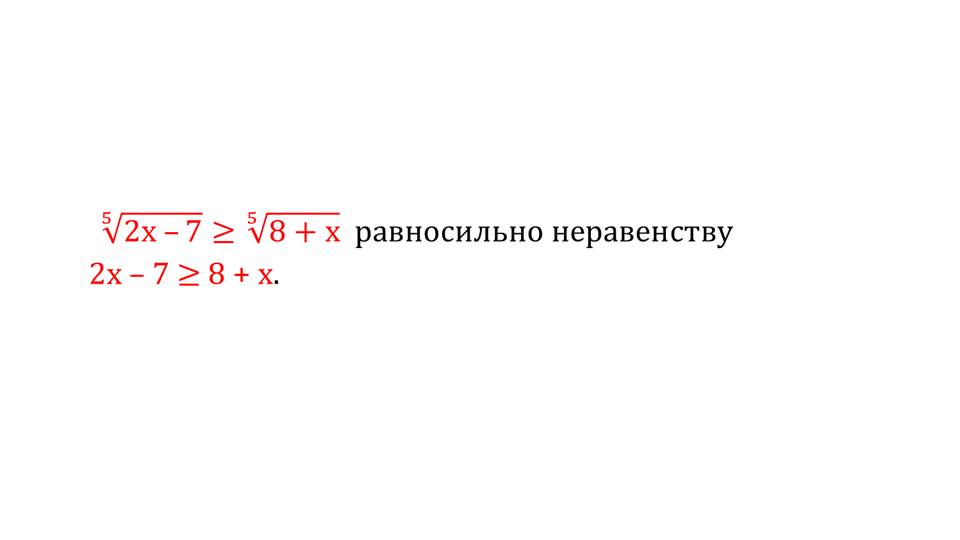



Еще один способ получить равносильные неравенства описан в теореме 2. В ней утверждается, что при возведении левой и правой частей неравенства в одинаковую нечетную степень, получается равносильное неравенство. Теорема так же, как и предыдущая, выделена в рамку, используемые в ней понятия окрашены в красный цвет для лучшего запоминания. Пример такого преобразования приведен на слайде 9. Дано неравенство 5√(2х-7) >=5√(8+х). при возведении обеих частей неравенства в степень 5, получается равносильное неравенство 2х-7>=8+х.
На слайде 10 сформулирована теорема, которая описывает неравенства, равносильные показательному. Отмечается, что показательное неравенство af(x)>ag(x) является равносильным неравенству f(x)>g(x) при а, большем 1, и равносильно неравенству f(x) <g(x) при положительном а, меньшем 1. Приводится пример равносильных неравенств - показательного 52х>5х+3 и соответствующего ему 2х>х+3, так как основание степени больше 1. Аналогично данному примеру, дается пример равносильных неравенств, если в показательном неравенстве основание степени меньше 1. Это неравенство 0,52х>0,5х+3 и равносильное ему 2х< х+3.




В теореме 4 рассматривается следующий способ получения равносильных неравенств – умножения обеих частей неравенства на выражение h(x), которое для всей области определения исходного неравенства будет положительным. При этом знак неравенства остается неизменным, и образуется равносильное неравенство h(x)f(x)> h(x)g(x). Теорема выделена для запоминания. К ней приводятся пример равносильных неравенств, образующихся таким способом. При умножении неравенства (3х+5)/√(х2+2) >(х-3)/√(х2+2) на выражение √(х2+2), получаем равносильное ему 3х+5>х-3. На слайде 15 дается пример как при умножении на выражение, которое образует только отрицательные значения, меняется знак неравенства на противоположный. При умножении (3х+5)/log0.4(х2+2) < =(х-3)/ log0.4 (х2+2) на выражение log0.4 (х2+2), получается равносильное неравенство 3х+5>=х-3.
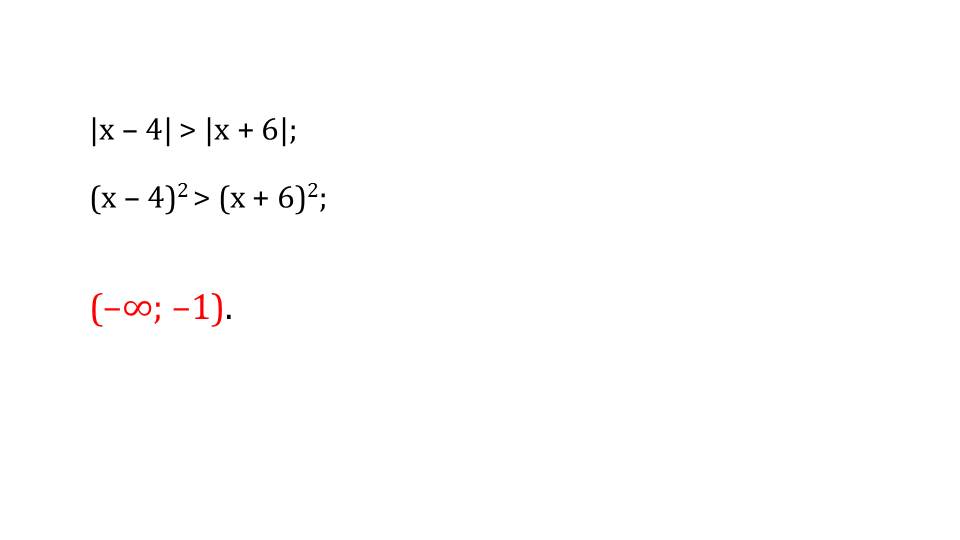



На слайде 16 описывается теорема 5, как образуются равносильные неравенства при возведении правой и левой частей неравенства в одинаковую четную степень. Условием такого преобразования служит неотрицательность частей неравенства в области определения. Равносильное неравенство получает вид f(x)n>g(x)n. Примером подобного преобразования неравенства в равносильное служит возведение в квадрат неравенства |х-4|>|х+6|. Равносильное неравенство принимает вид (х-4)2>(х+6)2. Отмечается, что решением такого неравенства будет промежуток (-∞;-1).
Теорема 6 отмечает особенности преобразования в равносильное логарифмического неравенства. В ней указано, что для положительных f(x) и g(x) неравенства logа f(x)> logа g (x) при а>1 равносильным будет неравенство f(x)>g(x), а при положительном а, меньшем 1, равносильным будет неравенство f(x) <g(x). На слайде 19 приводится пример получения равносильного неравенства неравенству log4 (3х-6)> log4(2x+4). Для его области определения (х>2) при основании логарифма, большем 1, равносильным будет неравенство 3х-6> 2x+4. Также аналогично рассматривается подобное неравенство с основанием логарифма, меньшим 1 - это log0,4 (3х-6)> log0,4(2x+4). Для него равносильным будет неравенство 3х-6< 2x+4.

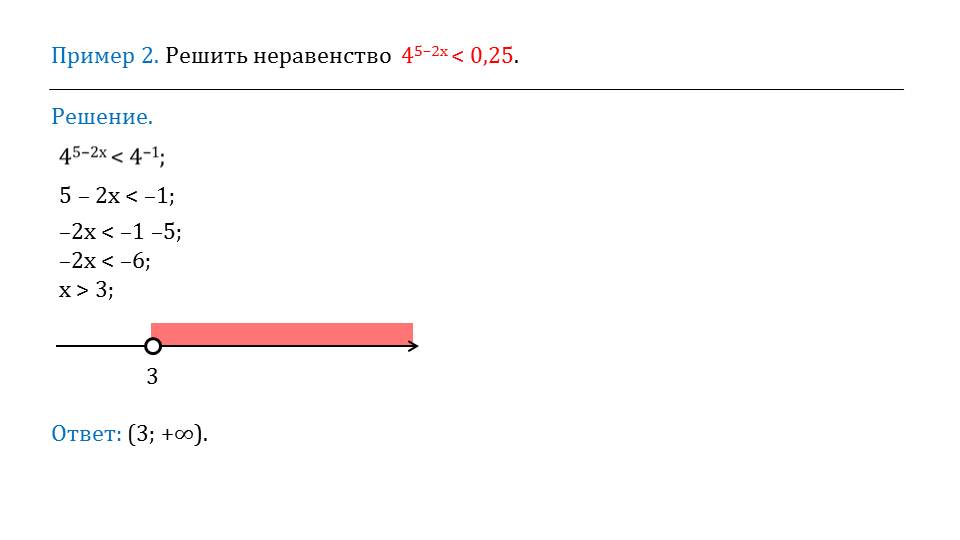

В конце презентации описывается решение трех примеров, в которых необходимо решить неравенства. В первом примере это неравенство 3х2-х<91-х. пользуясь правилом получения равносильного неравенства для показательного неравенства, получаем равносильное х2-х<2(1-х). решив данное неравенство, получаем промежуток (-2;1). Второй пример также представляет решение показательного неравенства 45-2х<0,25. Преобразовав правую часть неравенства в степень с основанием 4, получаем неравенство, для которого воспользуемся известным правилом для получения равносильного неравенства 5-2х<-1. Решив неравенство, получаем множество решений х>3. Соответствующее множество отмечается на числовой прямой. Третий пример представляет логарифмическое неравенство, которое решается равносильной системой двух соответствующих неравенств.
Презентация «Решение неравенств с одной переменной» может применяться для повышения эффективности традиционного школьного урока математики. Наглядное пособие может помочь учителю, осуществляющему дистанционное обучение, построить урок так, чтобы быстро достичь целей обучения. Также материал может быть рекомендован для самостоятельной работы учеников.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4299 |
| Номер материала | 1043 |