
Презентация "Решение неравенств с одной переменной. Системы и совокупности неравенств"

Краткое описание документа:
Презентация «Решение неравенств с одной переменной. Системы и совокупности неравенств» представляет наглядный учебный материал для проведения урока математики по данной теме. Ученики уже ознакомились со многими способами решения неравенств, поэтому решение систем и совокупностей неравенств не должно представить особой сложности. Однако использование презентации дает возможность более легко запомнить учебную информацию, быстрее овладеть методами решения систем и совокупностей неравенств.


Наглядное пособие помогает учителю быстрее достичь учебных целей, повысить эффективность обучения. Для лучшего запоминания теоретического материала используются рамки, указатели, выделение цветом. С их помощью выделяются важные понятия, акцентируется внимание на определениях и свойствах.
Сначала представляются теоретические сведения, оперирование которыми поможет овладеть навыками решения систем, совокупностей неравенств. На первом слайде отображается определение частного решения системы. На слайде, содержащем определение, указано, что таким решением является числовое значение переменной, обращающей неравенства всей системы в справедливые. Далее раскрывается понятие, что означает решить систему. Отмечается, что это означает найти все частные решения или доказать их отсутствие. На третьем слайде раскрывается смысл решения системы. Отмечено, что оно представляет собой пересечение множеств, составляющих решения отдельных неравенств. Ученикам напоминается алгоритм поиска решений системы, в которую входят неравенства, имеющие одну переменную. Он состоит из двух этапов – решения каждого неравенства, определения пересечения множеств. Далее рассматриваются примеры решений, выполняемых на основе данного алгоритма.


В примере 1 необходимо решить систему, в которую входят неравенства 7х-42<=0 и 2х-7>0. Каждое из неравенств решается простым переносом его членов из одной части в другую с изменением знака члена на противоположный. В результате вычислений получили два решения х<=6 и х>7/2. Для наглядности нахождения их пересечения, чертится числовая прямая, на которой отмечаются точки 7/2 и 6, заштриховывается промежуток, где располагается множество решений первого неравенство и другим цветом закрашивается промежуток, включающий множество решений второго неравенства. Решение системы оказывается окрашенным двумя цветами. Решение данной системы неравенств – промежуток (7/2;6].

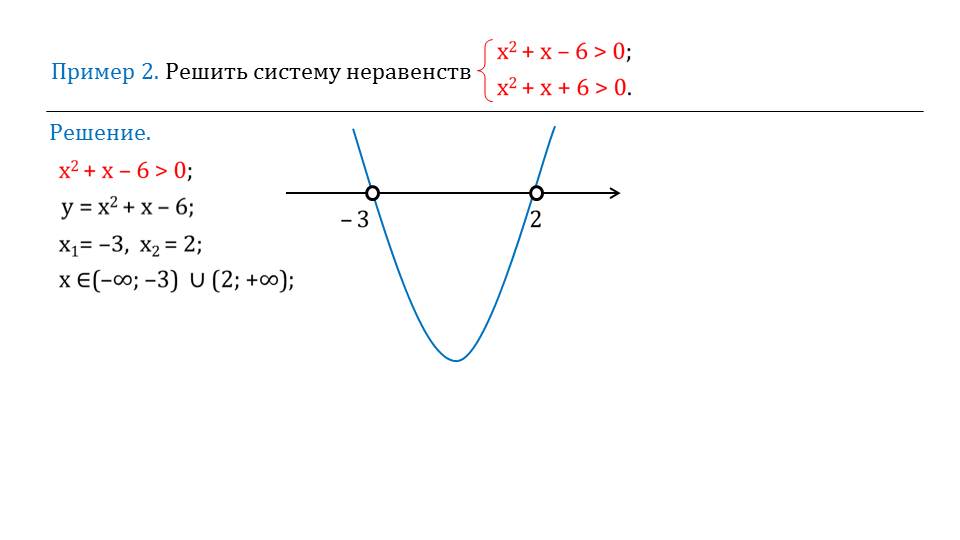
Во втором примере необходимо решить систему, состоящую из неравенств х2+х-6>0 и х2+х+6>0. Чтобы найти решение системы, сначала находятся решения отдельных неравенств. Определить решение неравенства х2+х-6>0 можно, найдя сначала решение уравнения х2+х-6=0. Это квадратное уравнение имеет решения х1=-3 и х2=2. Рядом с решением уравнения отмсечена числовая прямая, на которой отмечаются корни уравнения и промежутки, удовлетворяющие условию соответствующего неравенства. Решением неравенства является объединение промежутков (-∞;-3) и (2;+∞). Аналогично решается второе неравенство. Его дискриминант равен нулю, и любой действительный аргумент, подставленный в неравенство, обращает его в справедливое неравенство. В результате пересечения множеств решений обоих неравенств определяется решение системы. Решение данной системы (-∞;-3)U(2;+∞).


В третьем примере описывается решение неравенства log2(x2-13x+42)>=1. Сначала определяется область допустимых значений. Так как при возведении 2 в любую степень получается положительное число, вводится ограничение x2-13x+42>0. Чтобы найти решения неравенства, правую часть также представляют в виде логарифма 1= log22. Теперь для поиска решения исходное неравенство заменяется неравенством x2-13x+42>=2. Учитывая накладываемое ограничение на значения, получаем систему неравенств x2-13x+42>0 и x2-13x+42>=2. В результате получаем множество решений из двух промежутков (-∞;5]U[8;+∞).


Далее рассматривается совокупность неравенств, содержащих одну переменную, для которых ставится задание найти множество значений, каждое из которых будет решением неравенства из совокупности. Формулировка подобного задания охвачено в рамку, выделено понятие совокупности неравенств. Также на отдельном слайде отмечается, что значение переменной, удовлетворяющее требованию совокупности, называется ее частным решением. А все множество решений совокупности называется общим решением совокупности неравенств.


На слайде 12 представлен алгоритм решения совокупности неравенств. В нем указано, что на первом этапе необходимо решить неравенства, а затем найти объединение всех решений. На слайдах 14 и 15 приводятся примеры поиска решений совокупности. В примере 4 необходимо решить совокупность, состоящую из неравенств 0,2(2х-3)<x-2 и 5х-7>x-6. Решение отдельных неравенств не представляет сложности. В результате решения получаем два множества х>7/3 и х>1/4. На числовой прямой отмечаются различными цветами промежутки, включающие множества решений каждого неравенства. Объединением этих промежутков является промежуток (1/4;+∞). Это и есть решение совокупности неравенств.


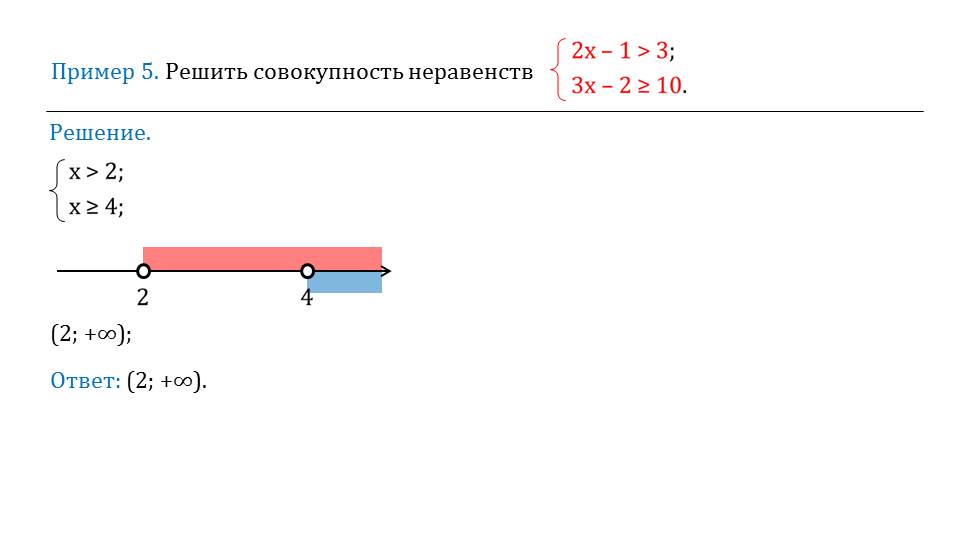
В примере 5 описывается решение совокупности неравенств 2х-1>3 и 3х-2>=10. В результате нахождения решений каждого неравенства получается два промежутка х>2 и х>=4. На числовой прямой отмечены данные промежутки. Также на числовой прямой можно увидеть, что объединением решений является промежуток (2;+∞).
Презентация «Решение неравенств, содержащих одну переменную. Системы, совокупности неравенств» рекомендуется для применения в качестве наглядного пособия на традиционном уроке математики по данной теме. Материал рекомендован также для использования в ходе дистанционного обучения. Пособие может помочь освоить тему ученикам, которым недостаточно времени школьного урока для глубокого понимания предмета.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4345 |
| Номер материала | 1044 |