
Презентация "Решение треугольников"

Краткое описание документа:
После изучения теоретической части теорем и тригонометрии, можно перейти к решению треугольников. Под решением треугольников подразумевают нахождение всех трех сторон и всех углов этой геометрической фигуры. Были рассмотрены такие теоремы, как теорема Пифагора, обобщенная теорема данной теоремы, теорема синуса. В прямоугольных треугольниках рассматривалось нахождение синуса и косинуса углов, исходя из данных катетов и гипотенузы.

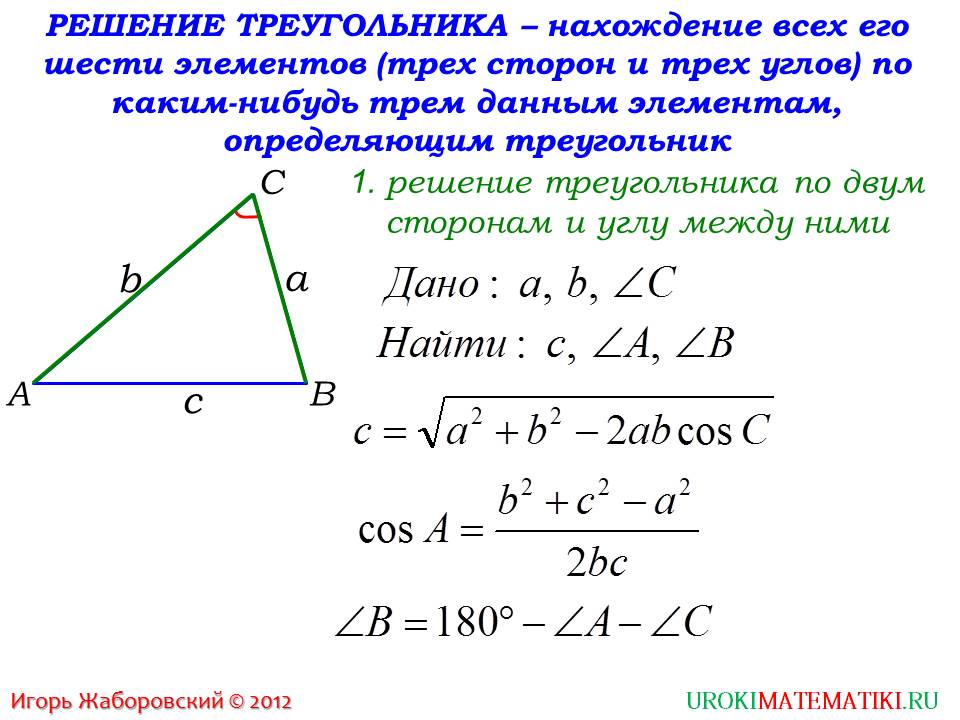
Первая задача, которая будет продемонстрирована вначале презентации, относится к решению треугольника по известным двум сторонам и углу между ними. Мы видим чертеж треугольника ABC, стороны, лежащие напротив углов A, B, С, обозначены, соответственно a, b, c. При рассматривании задач так будет намного удобнее. Далее, справа видим сокращенную запись условия задачи. С такой формой записи ученики уже сталкивались неоднократно. Согласно теореме косинусов, квадрат некоторой стороны равен разнице суммы квадратов остальных двух сторон и произведению этих сторон на косинус угла между ними. Для того, чтобы найти искомую сторону, необходимо вычислить квадратный корень от правой части. Оставшиеся два неизвестных угла можно найти исходя из того, что мы знаем, что сумма всех углов треугольника равна 180 градусам.
После того, как ученики рассмотрели этот слайд, учитель или репетитор может предложить им решить практический пример уже с числами. Подобные задачи очень часто встречаются в учебниках, так что можно просмотреть и их.
Перейдем к следующему слайду. Здесь будут продемонстрированы задачи, в которых рассматриваются треугольник, у которого известна некоторая сторона и два прилежащих к ней угла. Следует найти неизвестный угол и две оставшихся сторон. Дана сторона CA = a, и два прилежащий к ней угла, C и B. Найти неизвестный угол С очень просто, ведь знаем сумму всех углов треугольника. Неизвестные же стороны вычисляются по теореме синусов. Ученики могут вернуться к своим прежним записям и вспомнить их. Или же, могут просмотреть презентацию, в которой эта теорема рассматривалась.
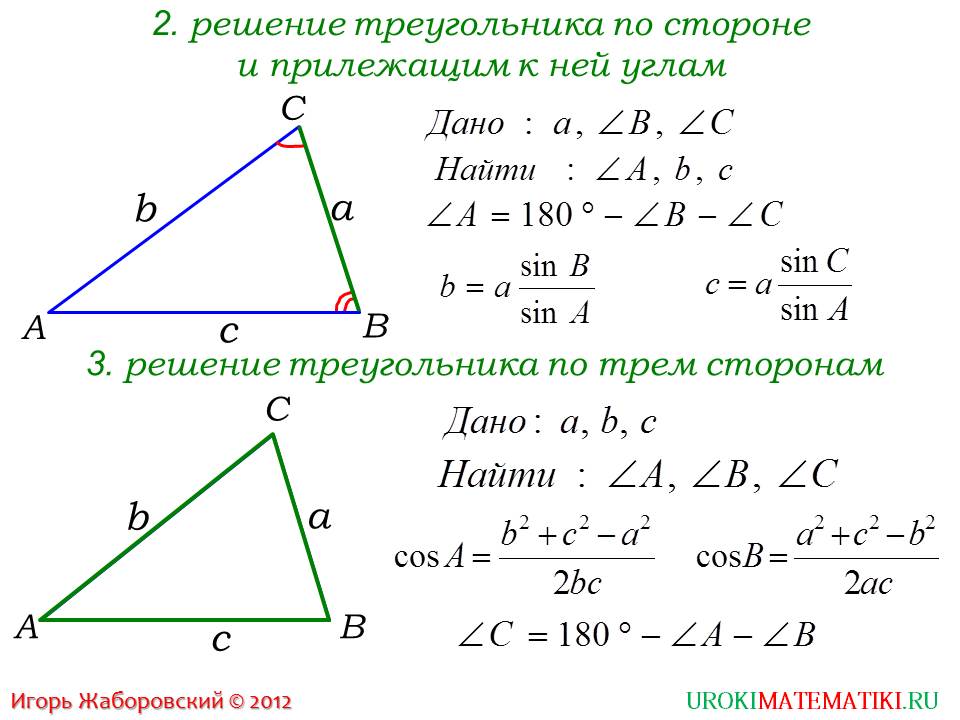
На этом же слайде рассматривается другая ситуация. Здесь даны три стороны треугольника ABC. Следовательно, необходимо найти тру угла. Решается данная задача, используя знания о косинусах, можно найти две стороны. Чтобы упростить задачу, третью сторону можно найти, вычитая оставшиеся две стороны из 180 градусов.
Третий слайд расскажет о решении интересно проиллюстрированной задачи. Мы видим ворота и футболиста. Футболист изображен у вершины, а ворота – это противолежащая сторона. Известны все три стороны треугольника. Необходимо найти неизвестный угол треугольника. Если футболист направит мяч в этом диапазоне, то он попадет в рамки ворот. Использует, которые даны по условию задачи.
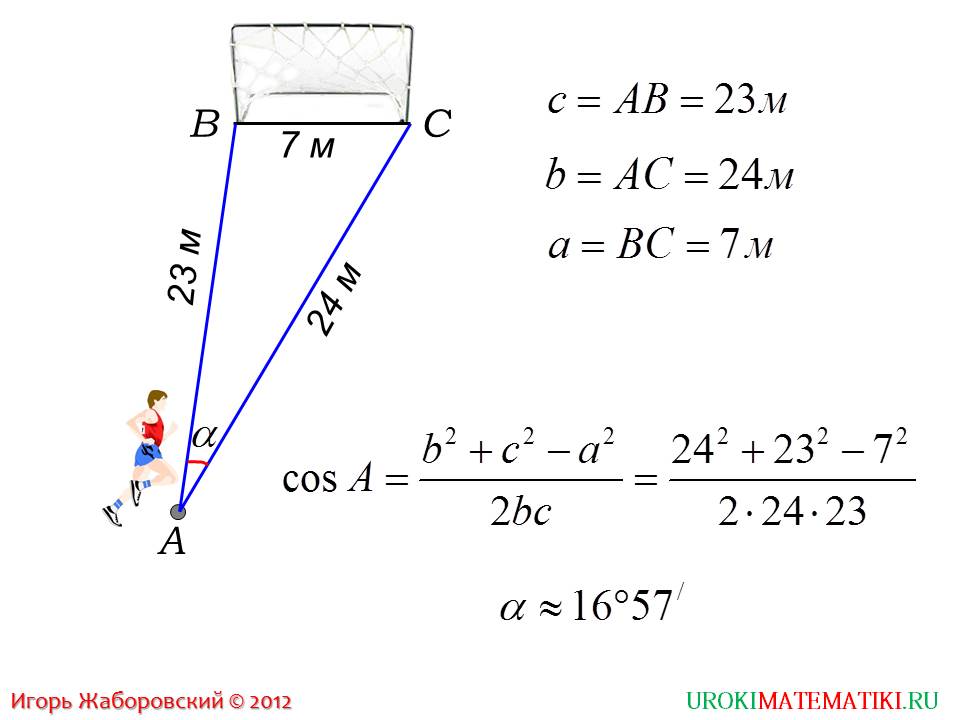
Если школьники поймут эти методы решения треугольников, то они смогут легко выполнить домашнее задание по данной теме. Также, у них не возникнут проблемы при выполнении контрольных и самостоятельных работ. Тема не является сложной, однако довольно объемная и включает в себя много формул, понятий и теорем.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5987 |
| Номер материала | 705 |