
Презентация "Синус и косинус разности аргументов"

Краткое описание документа:
Презентация «Синус и косинус разности аргументов» представляет формулы для преобразования косинуса и синуса разности аргументов, а также описывает решение пяти примеров различной сложности с применением данной формулы.
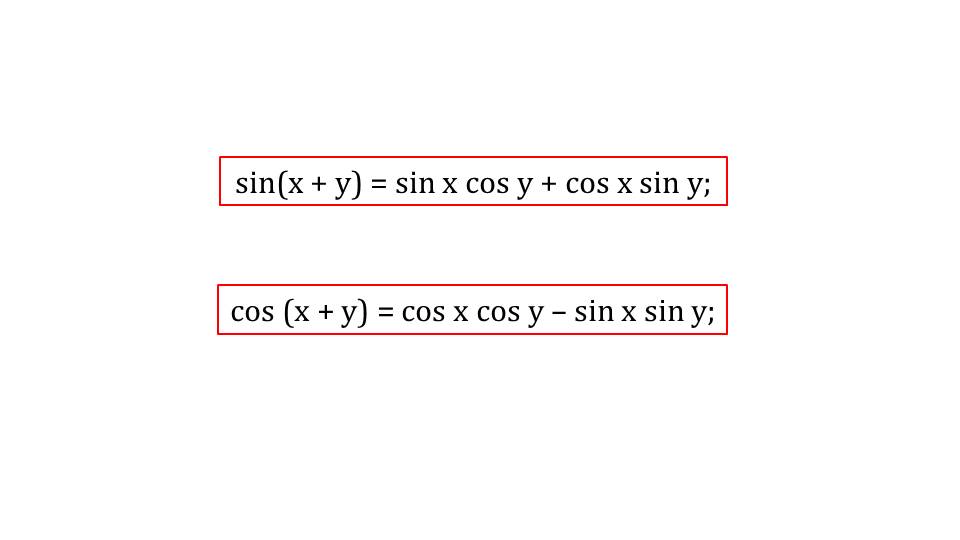
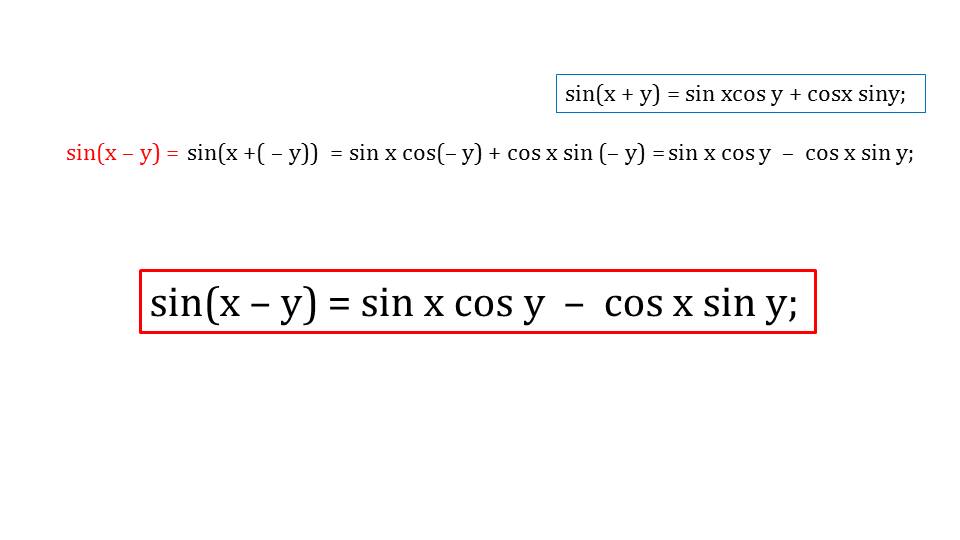
Задача презентации – наглядно представить учебный материал, способствуя лучшему запоминанию формул, формировать умения решать задания с применением формул для преобразования и упрощения нахождения решений.
Демонстрируемые формулы хорошо видны с любого места в классе, все производимые действия подаются последовательно, с выделением важных деталей решения. При помощи анимации подаваемая информация хорошо структурирована. Для лучшего запоминания формулы выделены в рамку, демонстрация решения дополняется таблицами значений тригонометрических функций. Применяемые в презентации приемы способствуют повышению эффективности урока.
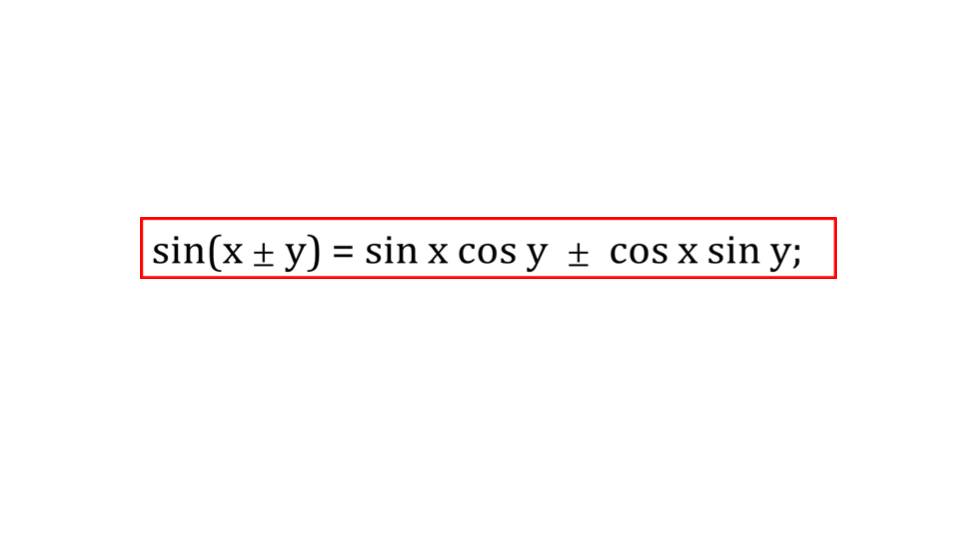

Демонстрация презентации начинается с представления формул синуса суммы аргументов и косинуса суммы аргументов. Формулы выведены на экран и заключены в рамку для лучшего запоминания. На втором слайде демонстрируется выведение формул синуса разности аргументов. За основу берется формула синуса суммы аргументов. При подстановке в качестве одного из слагаемых отрицательного значения (-у) правая часть формулы синуса суммы аргументов преобразуется в формулу sin (x-y)=sin x cos y - cos x sin y. При выведении формулы используется свойство синуса от отрицательного аргумента.
В третьем слайде на экран выводится общая формула, отображающая преобразование синуса суммы или разности аргументов в сумму или разность произведений синусов и косинусов аргументов.
Далее демонстрируется вывод формулы косинуса разности аргументов. За основу берется формула косинуса суммы аргументов, в которую подставляется отрицательное значение у. В преобразовании формулы используется свойство косинуса и синуса отрицательного аргумента. Так как cos (-y)= cos y, а sin (-y)= sin y, получаем в результате формулу косинуса разности cos (x-y)= cos x cos y+sin x sin y. Следующий слайд демонстрирует обобщенную формулу косинуса суммы или разности аргументов, которая отображает различие правой части формулы только знаком между произведениями, составляющими разность.
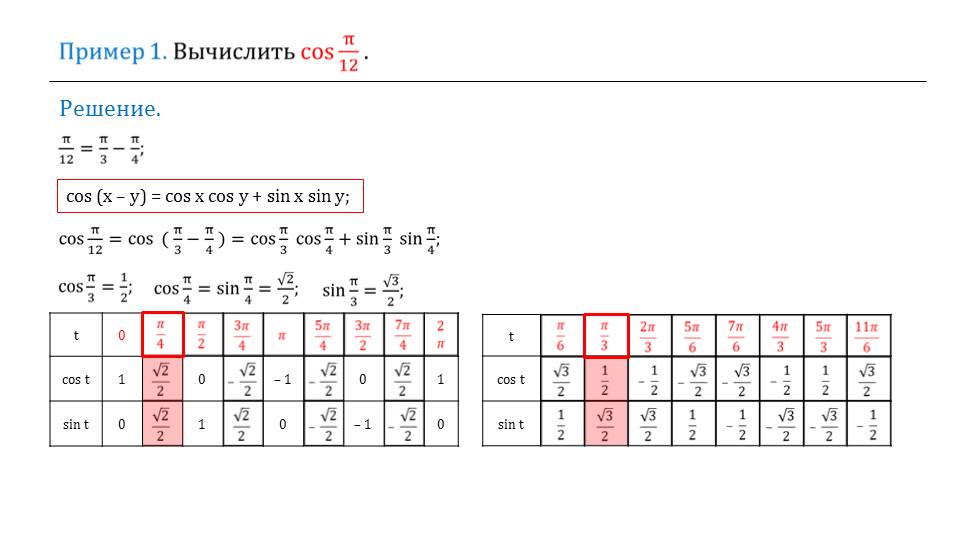
На слайде 6 описывается решение примера вычисления косинуса cos π/12. Очевидно, чтобы использовать табличные значения косинусов и синусов, можно представить данное выражение в косинус разности аргументов π/12=π/3-π/4. Для вычисления значения выражения применяем формулу косинуса разности и получаем сумму произведений cos π/3 cos π/4 + sin π/3 sin π/4. Подставив табличные значения cos π/3=1/2, cos π/4= sin π/4=√2/2, sin π/3=√3/2, получаем числовое выражение для вычисления значения косинуса (1/2)·(√2/2)+(√2/2)·(√3/2). Вычисли значение выражения, получаем cos π/12=(√2+√6)/4.
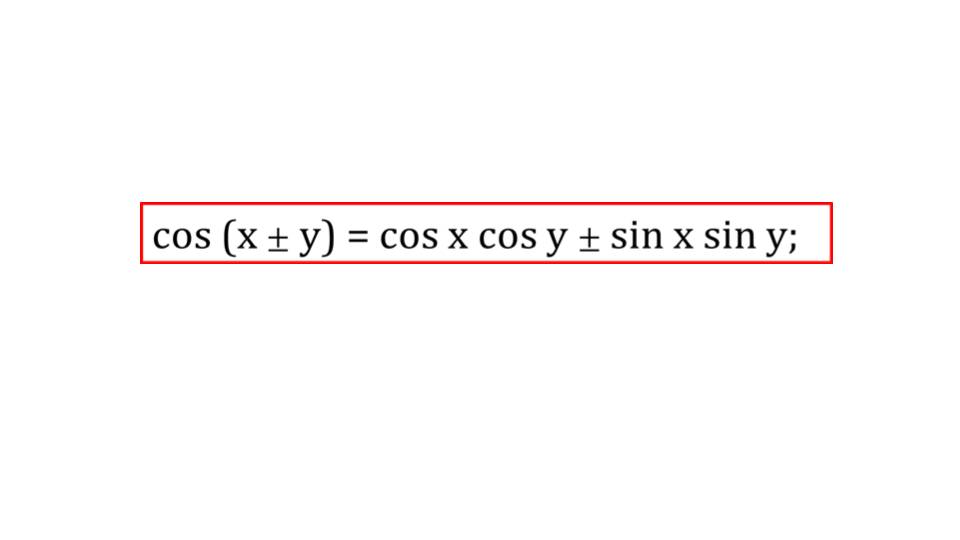
Далее описывается решение уравнения cos(2π-5x)=cos(π/2-5x). Чтобы решить данное уравнение, используется несколько формул, помогающих упростить данное выражение и использовать табличные значения синусов и косинусов – это cos(2π-α)=cosα, cos(π/2-α)=sinα, t=arctg α+πn. Используя формулу приведения, получаем cos 5x=sin 5x. После переноса правой части равенства влево и деления обеих частей уравнения на cos 5x, получаем cos 5x/ cos 5x - cos 5x/ cos 5x=0, что равнозначно 1-tg 5x=0. Это означает, что tg 5x=1, то есть 5х=arctg 1 + πn. Пользуясь табличными значениями тригонометрических функций, получаем значение аргумента 5х=π/4+πn или x=π/20+πn/5.
В примере 3 необходимо найти значение дроби, числитель и знаменатель которой представляют собой разности произведений косинусов и синусов (cos 75° cos 65° - sin 75° sin 65°)/( sin 85° cos 35° - cos 85° sin 35°). После применения формул синуса и косинуса разности аргументов, получаем дробь cos(75°+65°)/sin(85°-35°)=cos140°/sin50°. Используя формулу приведения cos(90°-α)=- sin α, преобразуем полученное выражение в отношение cos(90°+50°)/sin50°=-sin50°/sin50°=-1.
На слайде 11 описывается решение уравнения cos(π/4-x)+sin(π/4-x)=1. В уравнении встречаются косинус разности аргументов и синус разности аргументов. Применив к ним изученные формулы для преобразования, получаем cos(π/4-x)= cos π/4·cos x + sin π/4· sin х, а также sin(π/4-x)= sin π/4 cos x – cos π/4 sin x. Подставляя табличные значения косинусов и синусов π/4, при подстановке их в уравнение, получаем √2/2 cos x + √2/2 sin x +√2/2 cos x - √2/2 sin x=1. После приведения подобных слагаемых уравнение получает вид cos x =1/√2. Применяя формулу t=±arccos α + 2πk, значение x=±arccos√2/2+2πn. Пользуясь табличными значениями косинусов, получаем x=±π/4+2πn. Решение найдено.


Презентация «Синус и косинус разности аргументов» является наглядным пособием для проведения традиционного урока геометрии по данной теме. Наглядный материал также может пригодиться учителю, осуществляющему дистанционное обучение. Подробное описание решения примеров поможет глубже освоить материал ученикам самостоятельно.
Презентация «Синус и косинус разности аргументов» представляет формулы для преобразования косинуса и синуса разности аргументов, а также описывает решение пяти примеров различной сложности с применением данной формулы. Задача презентации – наглядно представить учебный материал, способствуя лучшему запоминанию формул, формировать умения решать задания с применением формул для преобразования и упрощения нахождения решений.
Демонстрируемые формулы хорошо видны с любого места в классе, все производимые действия подаются последовательно, с выделением важных деталей решения. При помощи анимации подаваемая информация хорошо структурирована. Для лучшего запоминания формулы выделены в рамку, демонстрация решения дополняется таблицами значений тригонометрических функций. Применяемые в презентации приемы способствуют повышению эффективности урока.
Демонстрация презентации начинается с представления формул синуса суммы аргументов и косинуса суммы аргументов. Формулы выведены на экран и заключены в рамку для лучшего запоминания. На втором слайде демонстрируется выведение формул синуса разности аргументов. За основу берется формула синуса суммы аргументов. При подстановке в качестве одного из слагаемых отрицательного значения (-у) правая часть формулы синуса суммы аргументов преобразуется в формулу sin (x-y)=sin x cos y - cos x sin y. При выведении формулы используется свойство синуса от отрицательного аргумента.


В третьем слайде на экран выводится общая формула, отображающая преобразование синуса суммы или разности аргументов в сумму или разность произведений синусов и косинусов аргументов.
Далее демонстрируется вывод формулы косинуса разности аргументов. За основу берется формула косинуса суммы аргументов, в которую подставляется отрицательное значение у. В преобразовании формулы используется свойство косинуса и синуса отрицательного аргумента. Так как cos (-y)= cos y, а sin (-y)= sin y, получаем в результате формулу косинуса разности cos (x-y)= cos x cos y+sin x sin y. Следующий слайд демонстрирует обобщенную формулу косинуса суммы или разности аргументов, которая отображает различие правой части формулы только знаком между произведениями, составляющими разность.
На слайде 6 описывается решение примера вычисления косинуса cos π/12. Очевидно, чтобы использовать табличные значения косинусов и синусов, можно представить данное выражение в косинус разности аргументов π/12=π/3-π/4. Для вычисления значения выражения применяем формулу косинуса разности и получаем сумму произведений cos π/3 cos π/4 + sin π/3 sin π/4. Подставив табличные значения cos π/3=1/2, cos π/4= sin π/4=√2/2, sin π/3=√3/2, получаем числовое выражение для вычисления значения косинуса (1/2)·(√2/2)+(√2/2)·(√3/2). Вычисли значение выражения, получаем cos π/12=(√2+√6)/4.
Далее описывается решение уравнения cos(2π-5x)=cos(π/2-5x). Чтобы решить данное уравнение, используется несколько формул, помогающих упростить данное выражение и использовать табличные значения синусов и косинусов – это cos(2π-α)=cosα, cos(π/2-α)=sinα, t=arctg α+πn. Используя формулу приведения, получаем cos 5x=sin 5x. После переноса правой части равенства влево и деления обеих частей уравнения на cos 5x, получаем cos 5x/ cos 5x - cos 5x/ cos 5x=0, что равнозначно 1-tg 5x=0. Это означает, что tg 5x=1, то есть 5х=arctg 1 + πn. Пользуясь табличными значениями тригонометрических функций, получаем значение аргумента 5х=π/4+πn или x=π/20+πn/5.
В примере 3 необходимо найти значение дроби, числитель и знаменатель которой представляют собой разности произведений косинусов и синусов (cos 75° cos 65° - sin 75° sin 65°)/( sin 85° cos 35° - cos 85° sin 35°). После применения формул синуса и косинуса разности аргументов, получаем дробь cos(75°+65°)/sin(85°-35°)=cos140°/sin50°. Используя формулу приведения cos(90°-α)=- sin α, преобразуем полученное выражение в отношение cos(90°+50°)/sin50°=-sin50°/sin50°=-1.
На слайде 11 описывается решение уравнения cos(π/4-x)+sin(π/4-x)=1. В уравнении встречаются косинус разности аргументов и синус разности аргументов. Применив к ним изученные формулы для преобразования, получаем cos(π/4-x)= cos π/4·cos x + sin π/4· sin х, а также sin(π/4-x)= sin π/4 cos x – cos π/4 sin x. Подставляя табличные значения косинусов и синусов π/4, при подстановке их в уравнение, получаем √2/2 cos x + √2/2 sin x +√2/2 cos x - √2/2 sin x=1. После приведения подобных слагаемых уравнение получает вид cos x =1/√2. Применяя формулу t=±arccos α + 2πk, значение x=±arccos√2/2+2πn. Пользуясь табличными значениями косинусов, получаем x=±π/4+2πn. Решение найдено.


Презентация «Синус и косинус разности аргументов» является наглядным пособием для проведения традиционного урока геометрии по данной теме. Наглядный материал также может пригодиться учителю, осуществляющему дистанционное обучение. Подробное описание решения примеров поможет глубже освоить материал ученикам самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4299 |
| Номер материала | 797 |