
Презентация "Скалярное произведение векторов"

Краткое описание документа:
Презентация на тему «Скалярное произведение векторов» представляет собой подбор материала для использования на школьных уроках в качестве основного учебного пособия. Применение данной презентации значительно повысит продуктивность учебного процесса и сделает его значительно более интересным за счет применения новых нестандартных методов преподнесения материала. Презентация имеет четкую и логичную структуру, что не вызовет проблем с восприятием материала, представленного на ней. На каждом слайде презентации представлены графические изображения, используя которые учащиеся значительно облегчают себе процесс усвоения информации. Тема, рассмотренная в презентации, является очень важной, поскольку имеет чрезвычайно широкое применение на практике при решении различных задач.


На слайде, который следует после слайда с названием презентации представлено определение скалярного произведения двух векторов. Суть определения заключается в том, что скалярным произведением двух векторов является произведение суммы их длин на косинус угла между ними. Понятие длины вектора и величины угла между двумя векторами должно быть известно учащимся из раннее изученного материала. Для того, чтобы определение лучше запомнилось, оно выделено более ярким цветом и другим шрифтом, что непроизвольно привлекает внимание учащихся. Формулы, которые необходимо знать, также выделены и бросаются в глаза. Далее на слайде рассматривается пример нахождения скалярного произведения двух векторов, угол между которыми равен девяносто градусов. Информация, которая находится в самом конце слайда, доводит до сведения учащихся, что скалярное произведение двух векторов, которые не являются нулевыми, будет равно нулю только в том случае, если они будут перпендикулярны друг другу. Знание основной формулы, применяемой для вычисления скалярного произведения двух векторов, является основополагающим и имеет чрезвычайно широкое применение на практике при решении всевозможных задач.
На третьем слайде презентации до учащихся доводится информация о том, что скалярное произведение двух векторов может быть положительным, в том случае, если угол между ними меньше девяноста градусов, и отрицательным, если угол между ними больше девяноста градусов. Для рассмотрения примеров приводится четкое и понятное графическое изображение, использование которого значительно упросит процесс изучения материала. На изображении представлено три вектора, имеющих различное положение по отношению друг к другу, а с правой стороны от изображения, представлено его буквенное объяснение. Также на данном слайде презентации представлено понятие скалярного квадрата вектора, суть которого заключается в том, что скалярным квадратом вектора является квадрат длины вектора.
На четвертом, заключительном слайде презентации вниманию учащихся предлагается разобрать еще один пример, чтобы окончательно закрепить пройденный материал и научиться применять его на практике. Согласно информации, представленной на данном слайде, произведение модулей вектора на косинус угла между ними соответственно равно произведению длин вектора без знака модуля.

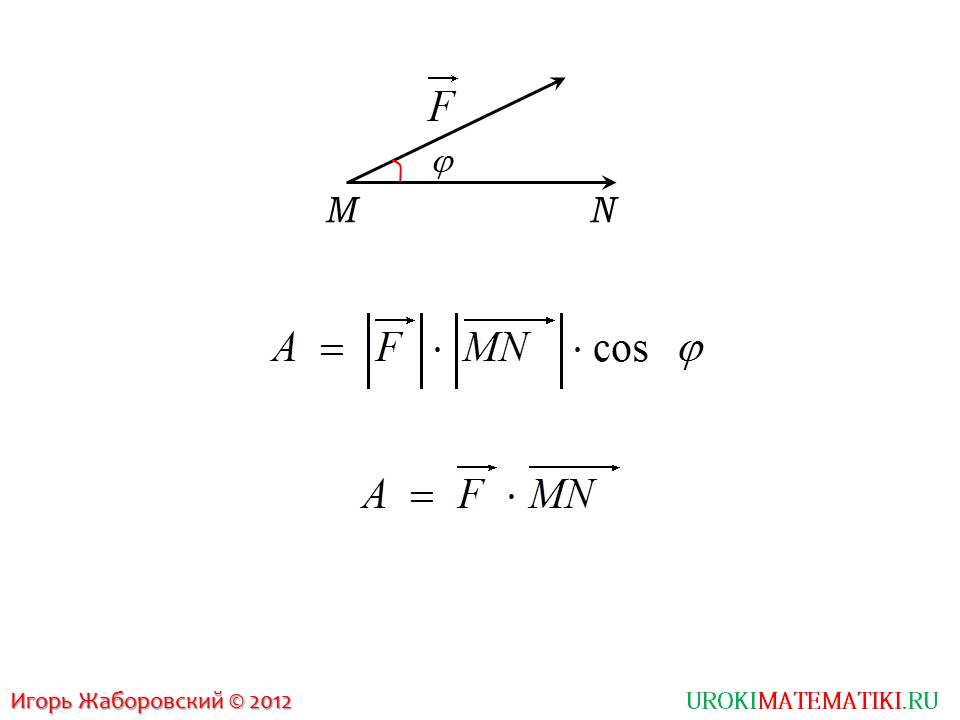
Данная презентация на тему «Скалярное произведение векторов» не содержит сложных визуальных эффектов, что не отвлекает внимание учащихся от основного учебного материала, который представлен на слайдах. Вся информация написана крупным шрифтом, а графические изображения являются четкими и понятными, что позволяет просматривать презентацию с помощью интерактивных досок даже в больших аудиториях с большим количеством учащихся.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5592 |
| Номер материала | 708 |