
Презентация "Способ сложения"

Краткое описание документа:
Для начала необходимо напомнить значение фразы «решить систему уравнений». Система уравнений с двумя переменными имеет частное решение в виде «х» нулевое и «у» нулевое. Они являются решением данной системы, если, подставляя «х» нулевое и «у» нулевое, уравнение становится верным числовым равенством. Но нам необходимо найти множество всех решений, где ключевым словом выступает слово «всех». Все методы, которые используются при решении системы уравнений, должны приводить именно к этому. Способ сложения, о котором говорится в данном уроке, является самым любимым для учащихся благодаря своему удобству.

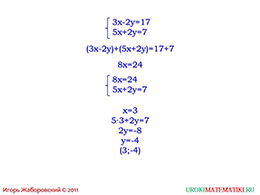
слайды 1-2 (Тема презентации "Способ сложения", пример)
Легче всего пользоваться равносильными или эквивалентными преобразованиями, которые не искажают решения, и приводят к равносильным системам (они имеют одно и то же множество решений). Именно таким лёгким методом и можно назвать метод сложения. Более того, используя различные методы по решению систем уравнений, проверка в конце не принципиальна, что делает их особенно приятными. Применяя данный метод, процесс решения выглядит следующим способом.
У нас есть система двух линейных уравнений с двумя переменными. Мы видим, что в первом уравнении есть минус два «у», а во втором – два «у», то есть мы можем сложить два уравнения, и данная переменная исчезнет, оставляя просто уравнение с одной переменной. Раскрываем скобки и получаем, что восемь «х» равняется двадцати четырём, а «х» равен трём. Подставляем в уравнение пять «х» плюс два «у» значение «х». Из этого уравнения мы находим, что два «у» равняется минус восьми, а значит «у» равен минус четырём. В результате получаем ответ, где «х» равен трём, а «у» - минус четырём. Мы получили единственное решение, но можно ли это предвидеть? Отчасти можно! У нас два линейных уравнения, коэффициенты переменных у них не пропорциональны, значит, прямые пересекаются, и мы имеем только одно решение в виде точки пересечения.


слайды 3-4 (алгоритм решения систем двух линейных уравнений с двумя переменными способом сложения, пример)
При решении данным методом стоит следовать определённому порядку:
- Если нет переменных, которые упростят систему сразу, то умножаем обе части уравнение на такое число, чтобы коэффициенты при одной переменной в уравнениях исчезли при сложении (то есть, чтобы они стали противоположными числами);
- Теперь мы смело можем сложить уравнения;
- Получаем уравнение с одной переменной и находим её значение;
- Подставляем полученное значение для того, чтобы найти, чему равна вторая переменная.
Рассмотрим следующий пример. Относительно сложная система, которую можно преобразовать, и получить более лёгкое решение. Умножим первое уравнение на минус три, а второе уравнение на два. Теперь у нас есть две противоположные переменные: минус шесть «х» и шесть «х», что означает, что мы можем сложить уравнения. В уравнении с одной переменной находим «у», которое равняется минус единице. Зная одну переменную, мы сразу можем найти вторую и получаем единственный ответ. Значит, это две прямые с точкой пересечения в координатах четыре и минус один.

слайд 5 (пример)
Теперь закрепим использование метода последним примером, решая следующую систему. Здесь необходимо сделать преобразование лишь с одним уравнением: второе умножить на минус два. Теперь, когда мы можем сложить уравнения, мы получаем одиннадцать «х» равное тридцати трём, а значит «х» равняется трём. Найдём последнюю координату, подставив значение первой переменной. Ответом данной системы является точка с координатами три и один, а если мы получили одно решение, значит, график функции представлен двумя прямыми, которые пересекаются в точке с уже упомянутыми координатами.
Теперь учащиеся владеют основоположным методом по решению системных уравнений.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4713 |
| Номер материала | 220 |