
Презентация "Свойства прямоугольного параллелепипеда"

Краткое описание документа:
Презентация «Свойства прямоугольного параллелепипеда»
Презентация «Свойства прямоугольного параллелепипеда» предназначена для формирования представления учеников об основных свойствах прямоугольного параллелепипеда. Это мультимедийное пособие, которое помогает учителю объяснить учащимся 9 класса особенности измерения диагоналей прямоугольного параллелепипеда, площади и объема. Презентация дана подробная, с доказательством важных утверждений, поэтому является полноценным инструментом для проведения эффективного урока геометрии.

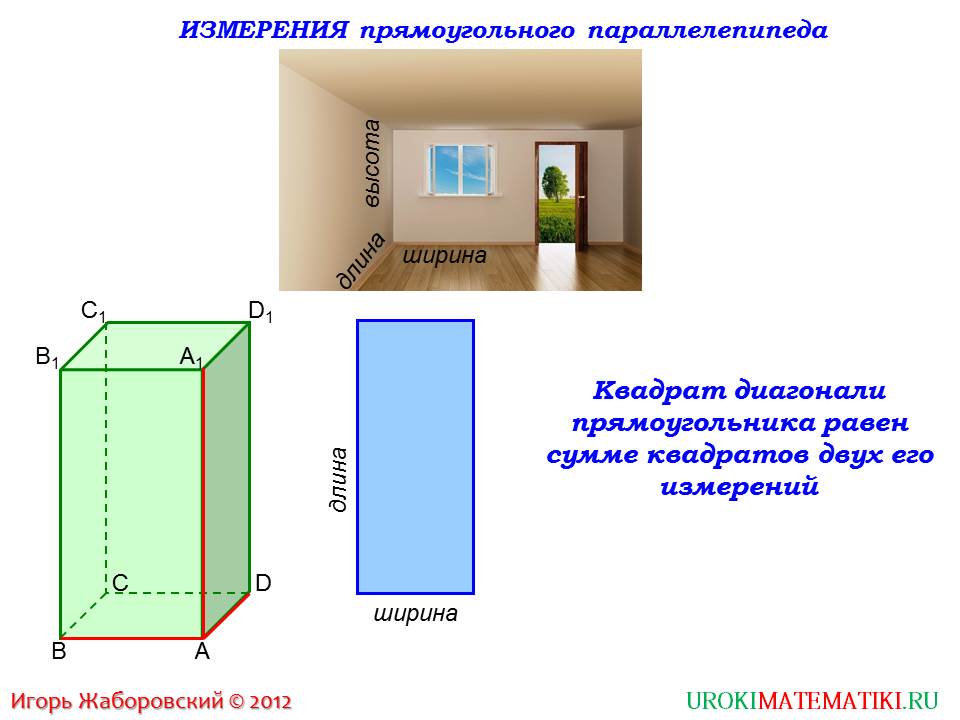
На момент изучения темы учащиеся уже знакомы с понятием прямоугольного параллелепипеда. Также имеют представление об объеме геометрического тела и его свойствах. После повторения базовых знаний ученик готов к освоению нового материала. Данная презентация обеспечивает наглядность изучаемого материала. Возможность изобразить геометрические тела в цвете помогает представить изучаемый материал в более понятном виде, облегчает понимание предмета. Анимированное изображение сопровождает построение, которое на школьной доске тяжело отобразить достаточно наглядно. Такая подача материала улучшает эффективность урока.
Презентация начинается с практического приложения изучаемого материала. На рисунке изображена комната, объем которой необходимо знать для решения многих практических задач – например, расчета тепловой мощности батарей отопления. Простая формула определения объема комнаты требует знания основных ее параметров – длины, ширины и высоты, которые отмечаются на рисунке. Ниже изображается геометрический аналог вышеприведенной задачи – параллелепипед со сторонами, обозначенными латинскими буквами ABCDA1B1C1D1. Аналогично уже достаточно хорошо изученному девятиклассниками понятию площади плоской фигуры – прямоугольника, рассматривается объем геометрического тела со сходными свойствами – прямоугольного параллелепипеда. На слайде напоминается свойство диагонали прямоугольника – квадрат ее равен сумме квадратов сторон, что вполне логично подтверждается теоремой Пифагора.
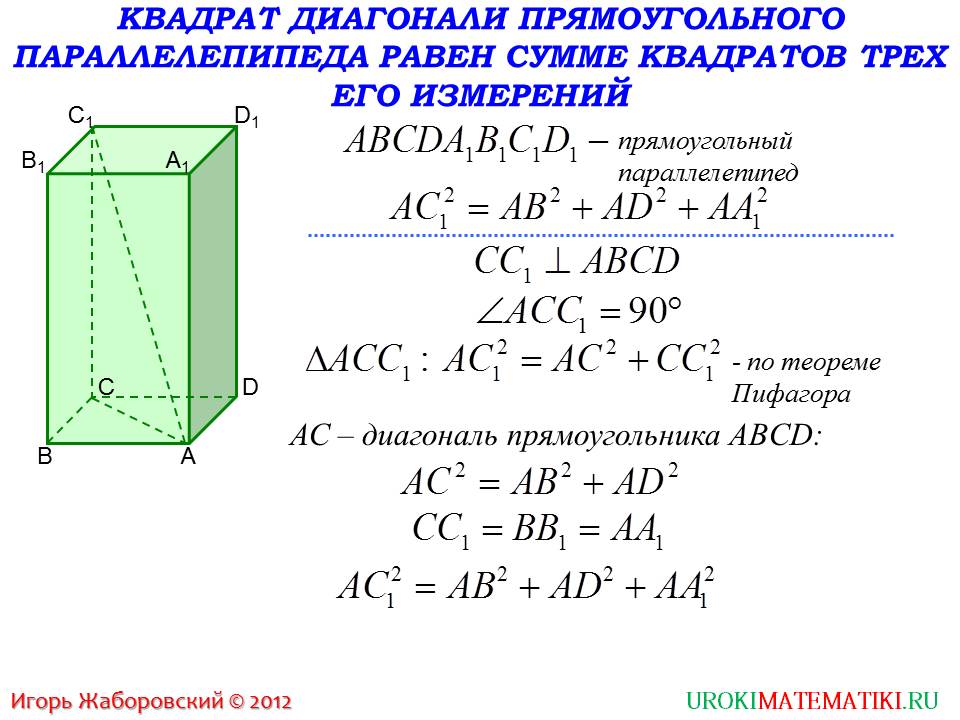
Теперь можно вывести подобное свойство для объемной фигуры – прямоугольного параллелепипеда. В начале слайда описывается утверждение, что квадрат диагонали данной фигуры будет равен сумме трех измерений фигуры. Данное утверждение требует доказательства, которое и приведено ниже на слайде. Доказательство сопровождается рисунком, на котором изображен прямоугольный параллелепипед ABCDA1B1C1D1. Утверждение, которое требуется доказать - . На рисунке отмечается диагональ параллелепипеда . Отмечается, что сторона СС1 направлена перпендикулярно плоскости прямоугольника ABCD. Соответственно, угол, образованный стороной и отрезком СА, будет 90°. Отмеченный прямоугольный треугольник предоставляет нам возможность использовать для доказательства теорему Пифагора, которая гласит, что что его гипотенуза будет равна сумме квадратов катетов . Наблюдая по рисунку, можно отметить, что отрезок СА является диагональю прямоугольника ABCD, который лежит в основании фигуры. Соответственно, этот отрезок можно выразить через стороны прямоугольника, также используя теорему Пифагора. В результате получаем, что данный отрезок удовлетворяет выражению . Подставляя его в выражение, соответствующее , получаем итоговое , означающее выполнение заключения утверждения, которое доказывается. Отмечается, что так как все боковые стороны данного прямоугольного параллелепипеда одинаковы, а углы по определению прямые, то данная формула будет верна для любой диагонали прямоугольного параллелепипеда.
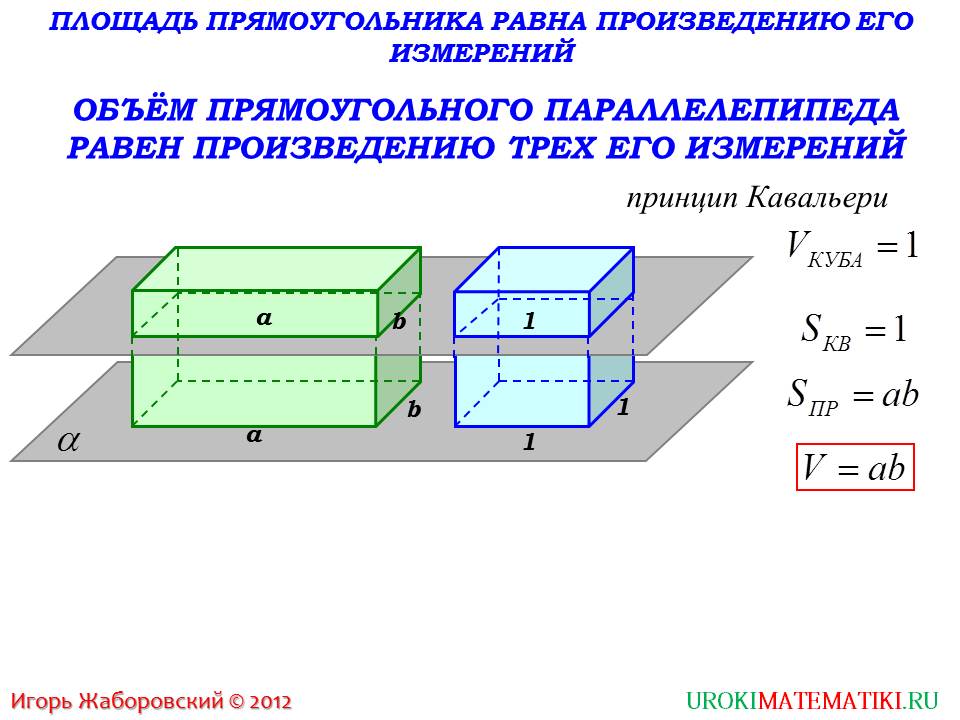
Следующий слайд рассматривает понятие объема прямоугольного параллелепипеда в частном случае – для прямоугольного параллелепипеда, выросшего из квадрата на 1. Для того, чтобы более глубоко понять и доказать утверждение, что объем прямоугольного параллелепипеда определяется как произведение трех его сторон, необходимо вспомнить, как находится площадь прямоугольника и принцип Кавальери. Так как площадь прямоугольника , а объем куба со сторонами 1 равен 1, согласно принципу Кавальери следует заметить, что объем параллелепипеда, который вырастает из куба на высоту 1, будет равен площади прямоугольной стороны. Соответственно, в данном случае . Такое представление объема помогает плавно перейти от понятия площади прямоугольника к объему прямоугольного параллелепипеда.
На следующем слайде рассматривается общий случай нахождения объема прямоугольного параллелепипеда. Имея прямоугольный параллелепипед, который вырос на 1 с объемом , рассматриваем случай роста прямоугольного параллелепипеда на произвольную величину с. Если в исходном параллелепипеде высота была 1, то соответствующая сторонам а и 1 площадь будет равна а. для второго прямоугольного параллелепипеда характерна площадь прямоугольника в основании , так как вторая сторона его будет – с. Соответственно, получаем объем прямоугольного параллелепипеда с произвольными сторонами а, bи c: . Если представить в данном параллелепипеде сторону b как высоту, то получаем еще одно общее представление объема как произведения площади прямоугольника в основании на высоту параллелепипеда . Словесное описание данного утверждения располагается внизу слайда для запоминания.
Презентация «Свойства прямоугольного параллелепипеда» подробно и понятно расписывает свойства прямоугольного параллелепипеда. Наглядные доказательства, живое представление рассматриваемого материала позволяют применять данную презентацию во всех формах учебного процесса. Она может быть рекомендована как наглядное пособие учителя на уроке в школе, так и в качестве пособия для дистанционного обучения и самостоятельного изучения предмета.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5991 |
| Номер материала | 729 |