
Презентация "Связь между координатами вектора и координатами его начала и конца"

Краткое описание документа:
Презентация «Связь между координатами вектора и координатами его начала и конца» формирует глубокое понимание механизма образования координат любых векторов на плоскости. Объяснение ведется просто и логично, начиная с наиболее простых понятий и постепенно усложняя материал, приводя к глубокому пониманию связи между координатами вектора и координатами его конца и начала. Данная тема урока включает повторение, как формируются координаты точки на плоскости, образование координат радиус-вектора и образование координат любого вектора на плоскости.
Тема геометрии 9 класса «Метод координат» сложная и требует внимательного изучения материала. При помощи данной презентации задачи учителя упрощаются. Используя наглядный материал, учителю легче научить учащихся применять методы векторной алгебры для решения геометрических задач. Решение задач таким способом вводит как вспомогательный инструмент прямоугольную систему координат, в которой векторы раскладываются по соответствующим координатным векторам. Используя такой аппарат, выполняется проведение операций над векторами.

Презентация имеет большое преимущество перед другими способами наглядности, так как предоставляет возможность использовать анимацию, повторяющую ход рассуждения или построения графиков. Для удержания внимания учеников используется выделение цветом, анимация изображений.
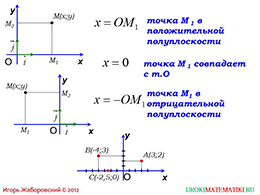
Начинается демонстрация презентации с построения системы координат XOY. На осях OX и OY отмечаются координатные векторы i ⃗ и j ⃗. На плоскости отмечается точка М с координатами х и у. При этом координата х определяется длиной отрезка ОМ1, который образуется при опускании перпендикуляра на ось ОХ. Отмечается, что так как координата х положительная, говорится о том, что точка М находится в положительной полуплоскости системы координат. Если значение координаты х=0, то точка совпадает с началом координат. Если координата х отрицательная, то это означает, что точка лежит в отрицательной полуплоскости системы координат. Все это можно наблюдать сразу при построении точек на координатной плоскости. Ниже на слайде приводится пример точек, расположенных в различных частях координатной плоскости с указанием их координат. Таким образом, учениками освоена основа данной темы – формирование координат точек на плоскости.
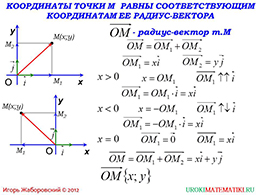
После рассмотрения координат точек на плоскости, демонстрируется связь между координатами точки и координатами ее радиус-вектора – простого случая, с которого можно начать рассматривать тему о координатах векторов. На рисунке можно увидеть, как формируется радиус-вектор, соединяющий точку начала отсчета и данную точку М. Отмечается, что вектор (OM) ⃗ – радиус-вектор точки М и представляет собой он сумму векторов (〖OM〗_1 ) ⃗ и (〖OM〗_2 ) ⃗. При этом первый вектор можно выразить через координату х, так как он коллинеарный оси ОХ и соответствующему ей координатному вектору i, а второй вектор выражается через координату у, так как он коллинеарный оси ОУ и соответствующему координатному вектору j. Вектор (〖OM〗_1 ) ⃗ образуется умножением единичного координатного вектора на значение длины отрезка ОМ1, поэтому характеризующее его выражение образуется произведением координаты точки М1 на единичный вектор. Подобным образом ниже рассматривается случай с координатой х, меньшей нуля. Отрицательная координата по абсолютному значению равна длине отрезка ОМ1, но ей присваивается знак «-», так как вектор (〖OM〗_1 ) ⃗, коллинеарный координатному вектору i, направлен противоположно ему. Соответственно, выражение для вектора (〖OM〗_1 ) ⃗ формируется как произведение соответствующей координаты точки М на единичный вектор i. Для точки М, которая совпадает с началом координат, вектор также будет нулевым. Подытоживая сказанное, при формировании выражения, соответствующего радиус-вектору (〖OM〗_ ) ⃗, в сумму векторов (〖OM〗_1 ) ⃗ и (〖OM〗_2 ) ⃗ подставляются соответствующие выражения через координаты и таким образом данный вектор характеризуется координатами векторов (〖OM〗_1 ) ⃗ и (〖OM〗_2 ) ⃗.
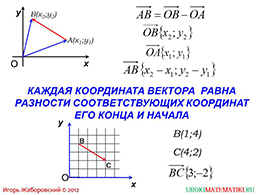
После рассмотрения базовых понятий и простых случаев можно перейти к собственно любому вектору, который в общем случае направлен от точки А(х;у) к точке В(х;у). Согласно правилу сложения векторов, вектор (AB) ⃗ образуется при вычитании из вектора (OB) ⃗ вектора (OA) ⃗. Каждый из векторов – радиус-векторы, координаты которых формируются в соответствии с рассмотренными выше правилами. В результате изучаемый вектор (AB) ⃗ формируется из попарной разности соответствующих координат. Ниже формулируется правило, выделенное для облегчения запоминания о том, что каждая координата представляет собой разность соответствующих координат конца и начала вектора. Для закрепления изученного демонстрируется пример вектора (BC) ⃗ с определенными координатами конца и начала и каковы в результате простых вычислений будут координаты самого вектора.
Данная презентация понятно и подробно рассматривает изучаемую тему и подводит к глубокому пониманию материала, поэтому может быть рекомендована для самостоятельного изучения и эффективно использоваться для дистанционного обучения. Для учителя на уроке она также является очень удобным инструментом для достижения целей урока.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7033 |
| Номер материала | 694 |